数学の疑問素因数分解のやり方。5つのステップで分かる素因数分解問題の解き方とコツ
2018年2月15日 Tooda Yuuto アタリマエ！
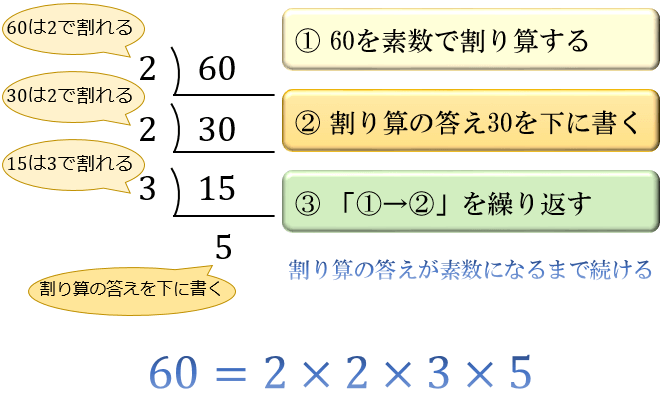
ある整数を「素数のかけ算」の形に変形することを素因数分解(prime factorization)と言います。 たとえ …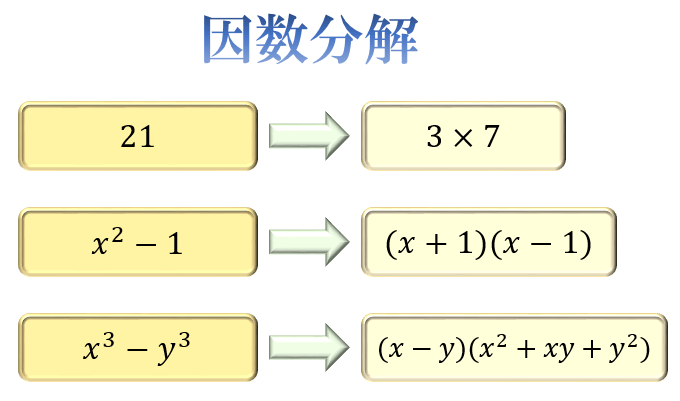
数学の疑問因数分解の問題の解き方とコツ。2乗・3乗公式とたすきがけ
2017年11月8日 Tooda Yuuto アタリマエ！
数の中には「2つ以上の数のかけ算」に変形できるものがたくさんあります。
例えば \(x^2-1\) は \((x+1)(x-1)\ …
数学の疑問ルート２ルート３ルート５ルート７のゴロ合わせ【素数の平方根の筆算の仕方】
2017年11月1日 Tooda Yuuto アタリマエ！
\(\sqrt{2}=1.41421356\cdots\) は「一夜一夜に人見頃」と覚えます。
これは「一晩経つごとに桜の花が開い …
数学の疑問有理数と無理数の違い。ルート２が無理数であることの証明
2017年10月23日 Tooda Yuuto アタリマエ！
今回は、有理数と無理数について。 有理数は英語で Rational Number 、無理数は英語で Irrational Nu …
数学の疑問べき乗とは何か。ゼロ乗・マイナス乗・分数乗・無理数乗ってどういう意味？
2017年10月20日 Tooda Yuuto アタリマエ！
\(2^3\) や \(3^4\) に限らず、\(3^{-2}\)・\(5^\frac{1}{2}\)・\(8^π\) といった値も …
数学の疑問累乗とは。その意味と計算方法を解説【底・指数とは何か】
2017年10月18日 Tooda Yuuto アタリマエ！
同じ数をくり返しかけ算したもののことを、累乗と言います。
たとえば \(3\) を \(4\) 回かけ合わせた場合、\(3×3×3×3 …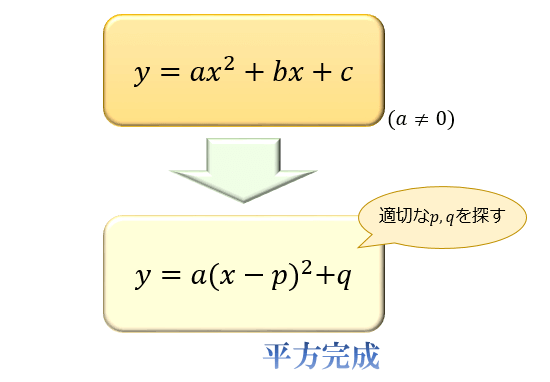
数学の疑問平方完成のやり方と平方完成するメリットについて
2017年10月10日 Tooda Yuuto アタリマエ！
\(ax^2+bx+c\) の形の二次式を \(a(x-p)^2+q\) の形に変形することを平方完成と言います。 \(m …
数学の疑問フィボナッチ数列とは。一般項の証明・黄金比との関係について
2017年10月6日 Tooda Yuuto アタリマエ！
フィボナッチ数列は「隣り合う2つの数を合計すると次の数になる数列」です。
英語では Fibonacci Sequence. 名前の …
数学の疑問必要条件と十分条件の違い。その意味と分かりやすい覚え方
2017年9月29日 Tooda Yuuto アタリマエ！
「\(P\) ならば \(Q\)」が成り立つとき、記号では\(「P→Q」\)と書き
\(Q\) は \(P\) であるための必要条件
…
数学の疑問微分係数と導関数の違いとその使い分け
2017年9月27日 Tooda Yuuto アタリマエ！
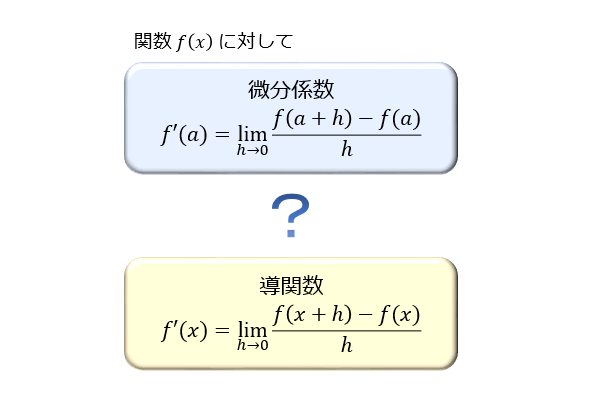
微分の勉強をするときに混同してしまいやすい2つの数。微分係数と導関数。 微分係数と導関数はその定義式がよく似ているので「なぜ使い分けるのか」「どう使い分けるのか」が分 …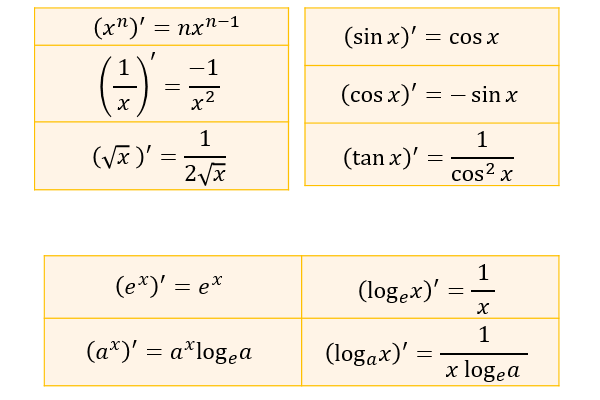
数学の疑問微分の公式一覧
2017年9月27日 Tooda Yuuto アタリマエ！
このページでは、よく使う微分の公式をまとめています。 (さらに…) …
数学の疑問微分とは何かを分かりやすくするコツは「速度」にある
2017年9月20日 Tooda Yuuto アタリマエ！
関数 \(f(x)\) に対して、以下の式で表される導関数 \(f'(x)\) を求めることを「関数 \(f(x)\) を微分する」 …
数学の疑問平方根(ルート)の計算方法まとめ。おさえておくべき4つのポイント
2017年9月20日 Tooda Yuuto アタリマエ！
このページでは、平方根の足し算・引き算・かけ算・割り算を4つのポイントに分けて解説していきます。 (さらに&hellip …
統計学中央値と四分位数の求め方。四分位範囲・四分位偏差とは何か？
2017年8月28日 Tooda Yuuto アタリマエ！
中央値（メジアン）とは、データを大きさの順に並べたときに全体の中央に位置する値のことです。 同じく、データを大きさの順に並べた …