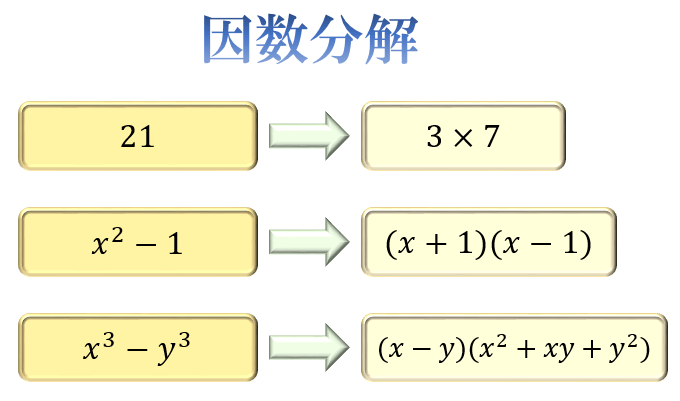
数の中には「2つ以上の数のかけ算」に変形できるものがたくさんあります。
例えば \(x^2-1\) は \((x+1)(x-1)\) というかけ算に変形できますよね。
このように特定の数を「2つ以上の数のかけ算」に変形することを、因数分解と言います。
「因数分解する」を英語で言うと、Resolve into factors 。
「売上=価格×販売数」や「距離=速度×時間」のように「ある数値がどんなfactor(要因)から成り立っているか」を分解して考えることは、どんな分野でも欠かす事のできない重要な思考法です。
今回は、そんな因数分解の解き方のコツを見ていきましょう。
因数分解と展開の違い。2乗・3乗の公式
因数分解は、「式の展開」の反対に相当する変形です。

カッコの中を1つずつかけ算していけば求まる「展開」と異なり、因数分解は公式を知らないと解き方の検討がつかないケースもあります。


因数分解の問題と解き方
因数分解の問題は、主に以下の手順で解くのがオススメです。
- 共通する因数でくくる
- 因数分解の公式を当てはめる
- 因数の1つが \(0\) になるような \(x\) を元の式に代入して正しいかチェックする
具体的に、例題を見ていきましょう。
問①.\(2x^2-12x+18\) を因数分解してください

\(x^2-6x+9\) の形を見た瞬間に「2倍したら \(-6\)、2乗したら \(9\) 」となる数 \(-3\) が頭に思い浮かぶようになれば完璧です。
問②.\(3x^2-12x-15\) を因数分解してください

\(x^2-4x-5\) の形を見たときに「足したら \(a+b=-4\)、かけたら \(ab=-5\) 」となる \(a,b\) の組み合わせを考えるのがコツです。
\((a=-5,b=1\) または \(a=1,b=-5)\)
たすきがけの公式
\(3x^2-7x+2\) のように「共通する因数でくくっても、\(x^2\) の係数が \(1\) にならない式」を因数分解する場合には、「たすきがけ」というテクニックを使います。
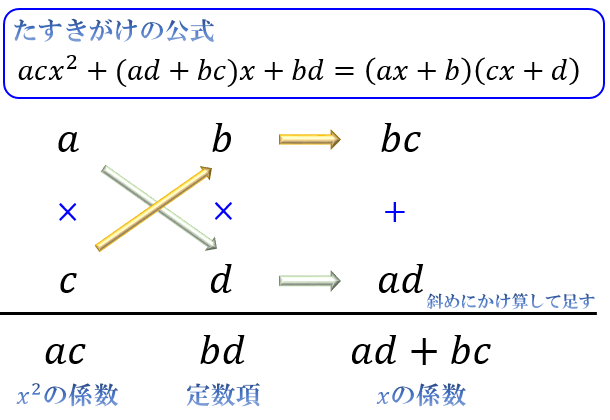
文字だけだとピンと来にくいと思うので、具体例を通じてやり方を見ていきましょう。
問③. \(3x^2-7x+2\) を因数分解してください
- \(x^2\) の係数が \(3\) なので、積が \(3\) になる2つの正の数 \(a,c\) を探す \((3,1)\)
- 定数項が \(2\) なので、積が \(2\) になる2つの数 \(b,d\) を探す \((1,2),(-1,-2)\)
- \(x\) の係数が \(-7\) なので、斜めにかけ算して足した答えが \(-7\) になる組み合わせを探す
- \((ax+b)(cx+d)\) に因数分解できる
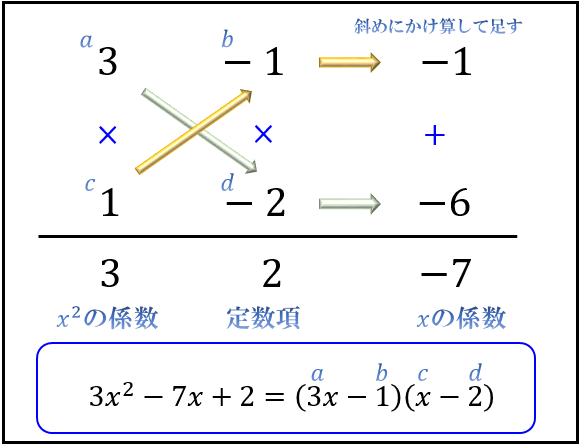
\(a=3\),\(b=-1\),\(c=1\),\(d=-2\) の組み合わせで「斜めにかけ算して足した答えが \(-7\) になる」ので
\(3x^2-7x+2=(3x-1)(x-2)\)
と求まります。
問④. \(6x^2+5x-21\) を因数分解してください
- \(x^2\) の係数が \(6\) なので、積が \(6\) になる2つの正の数 \(a,c\) を探す
- 定数項が \(-21\) なので、積が \(-21\) になる2つの数 \(b,d\) を探す
- \(x\) の係数が \(5\) なので、斜めにかけ算して足した答えが \(5\) になる組み合わせを探す
- \((ax+b)(cx+d)\) に因数分解できる
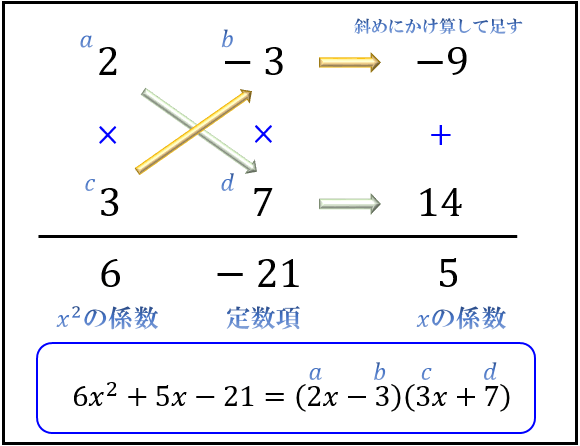
\(a,c\) の組み合わせは \((1,6)\) か \((2,3)\)
\(b,d\) の組み合わせは \((1,-21)\) か \((-1,21)\) か \((3,-7)\) か \((-3,7)\)
これらを上手く組み合わせて「斜めにかけ算して足した答えが \(5\) になる組み合わせ」を探します。
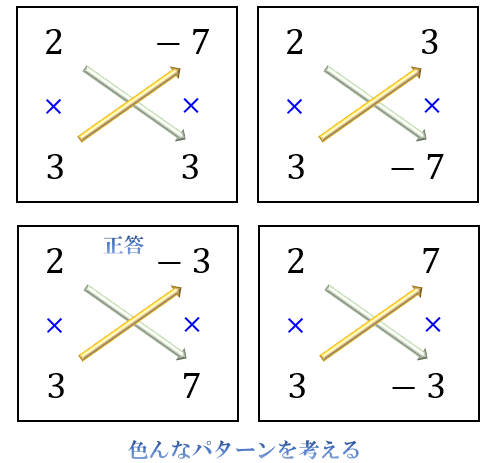
\(a=2\),\(b=-3\),\(c=3\),\(d=7\) の組み合わせで「斜めにかけ算して足した答えが \(5\) になる」ので
\(6x^2+5x-21=(2x-3)(3x+7)\)
と求まります。
xの2乗,yの2乗,xy,x,yを含む因数分解
問⑤.\(2x^2+3y^2+7xy+x-7y-6\) を因数分解してください
このタイプの問題は、以下の手順で解くのがオススメです。
- \(x\) の2乗、1乗、0乗の項ごとに分ける
- \(x\) の0乗の項を \(y\) で因数分解する
- \(y\) で因数分解した結果を定数項と考えて、たすきがけを行う

結果、\((2x+y-3)(x+3y+2)\) と求まりました。