このページでは、平方根の足し算・引き算・かけ算・割り算を4つのポイントに分けて解説していきます。
①ルートの中身を簡単にする
分数を書くときは \(\dfrac{6}{4}=\dfrac{3}{2}\) のように可能な限り「約分」をしますよね。
それと同じで、平方根を使って数を表すときはルートの中身を可能な限り小さな自然数にします。

\(\sqrt{28}\) のルートの中身を可能な限り簡単にしてください
\(\sqrt{28}=\sqrt{2×2×7}=2\sqrt{7}\)
\(\sqrt{180}\) のルートの中身を可能な限り簡単にしてください
\(\sqrt{180}=\sqrt{2^2×3^2×5}\)
\(=2×3×\sqrt{5}=6\sqrt{5}\)
②平方根の足し算・引き算
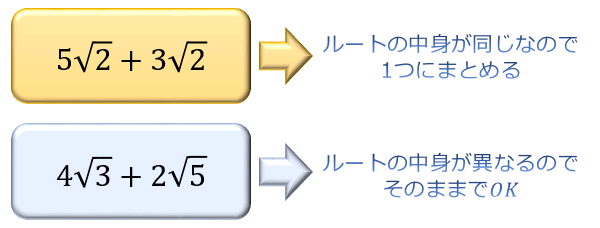
平方根の足し算と引き算は、ルートの中身が同じ数を1つにまとめます。
パッと見は中身が異なる場合でも、ルートの中身を簡単にすると同じになるケースもあるので、ルートの中身を可能な限り簡単にしてから足し算・引き算を行います。
\(\sqrt{50}+\sqrt{18}\) を計算してください
\(\sqrt{50}+\sqrt{18}=\sqrt{5^2×2}+\sqrt{3^2×2}\)
\(=5\sqrt{2}+3\sqrt{2}=(5+3)\sqrt{2}=8\sqrt{2}\)
\(7\sqrt{3}-\sqrt{27}\) を計算してください
\(7\sqrt{3}-\sqrt{27}=7\sqrt{3}-\sqrt{3^2×3}\)
\(=7\sqrt{3}-3\sqrt{3}=(7-3)\sqrt{3}=4\sqrt{3}\)
\(3\sqrt{3}+\sqrt{3}+5\sqrt{5}-3\sqrt{5}\) を計算してください
\(3\sqrt{3}+\sqrt{3}+5\sqrt{5}-3\sqrt{5}\)
\(=(3+1)\sqrt{3}+(5-3)\sqrt{5}\)
\(=4\sqrt{3}+2\sqrt{5}\)
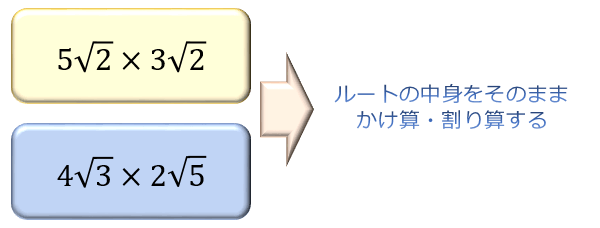
③平方根のかけ算・割り算
平方根のかけ算と割り算は、ルートの中身をそのままかけ算・割り算します。
\(5\sqrt{2}×3\sqrt{2}\) を計算してください
\(5\sqrt{2}×3\sqrt{2}=(5×3)\sqrt{2×2}\)
\(=15×2=30\)
\(4\sqrt{3}×2\sqrt{5}\) を計算してください
\(4\sqrt{3}×2\sqrt{5}=(4×2)\sqrt{3×5}=8\sqrt{15}\)
\(4\sqrt{6}÷2\sqrt{2}\) を計算してください
\(4\sqrt{6}÷2\sqrt{2}=(4÷2)\sqrt{6÷2}=2\sqrt{3}\)
\(4\sqrt{30}×3\sqrt{21}÷6\sqrt{14}\) を計算してください
\(4\sqrt{30}×3\sqrt{21}÷6\sqrt{14}\)
\(=(4×3÷6)\sqrt{30×21÷14}\)
\(=2\sqrt{45}=2\sqrt{3^2×5}\)
\(=2×3×\sqrt{5}=6\sqrt{5}\)
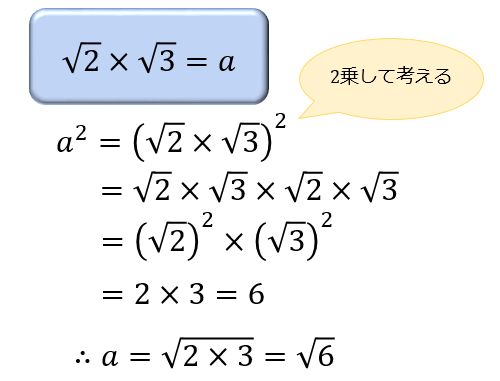
④分母を有理化する
分数の分母に平方根がある場合は、計算しやすくするために分母と分子に同じ数をかけることで分母に平方根を含まない形に変形します。
この変形のことを分母の有理化といいます。
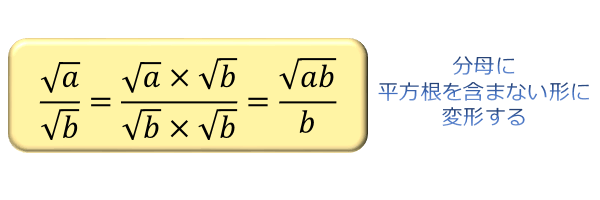
\(\dfrac{2}{\sqrt{3}}\) と \(\dfrac{\sqrt{3}}{2\sqrt{7}}\) について分母の有理化をしてください
\(\dfrac{2}{\sqrt{3}}=\dfrac{2×\sqrt{3}}{\sqrt{3}×\sqrt{3}}=\dfrac{2\sqrt{3}}{3}\)
\(\dfrac{\sqrt{3}}{2\sqrt{7}}=\dfrac{\sqrt{3}×\sqrt{7}}{2\sqrt{7}×\sqrt{7}}=\dfrac{\sqrt{21}}{14}\)
平方根の計算まとめ
- 平方根の中身は可能な限り簡単にする
- 平方根の足し算・引き算はルートの中身が同じ数を1つにまとめる
- 平方根のかけ算・割り算はルートの中身をそのまま計算する
- 分母に平方根があるときは有理化する