推測統計学は、母集団から無作為に抽出した標本のデータを調べることで、母集団の性質・特徴を推定する学問です。
たとえば、日本の成人男性の平均身長を求めたい場合、日本にいるすべての成人男性のデータを集めようとすると時間とコストがかかりすぎてしまいますよね。

そこで、全国からランダムに抽出した標本(サンプル)のデータから「日本の成人男性の平均身長は何cm~何cmだと推定できるのか」や「誤差0.1cm以内の正確な推定をしたい場合には、ランダムに何人分データを調べれば良いのか」を計算する。
それが推測統計学の役割の1つです。
このように、データの特徴の推定を始めさまざまな領域で活躍している推測統計学ですが、いざ勉強しようと思ったときに少し困ることがあります。
それは、「言葉の省略」です。
たとえば一口に標準偏差と言っても、推測統計学では『母標準偏差』『標本標準偏差』『不偏分散による標準偏差』『不偏標準偏差』『標本平均の標本分布の標準偏差(=標準誤差)』と、その言葉が指す対象はさまざま。

しかし、統計学の教科書ではこれらを省略して「標準偏差」とだけ表記することが多いため、初学者が苦戦しやすいポイントとなっています。
どの標準偏差を指すのかは基本的に文脈や記号で判断することになるのですが、書籍によって書き方が異なっているケースもあり、その対応関係を理解していないと「いま、何を勉強しているのか」が分からなくなる危険性があるのです。
そこで今回は、推測統計学でよく出てくる用語の対応関係について軽く書いていきます。
1人でも多くの方に推測統計学の予習・復習に利用していただければ幸いです。
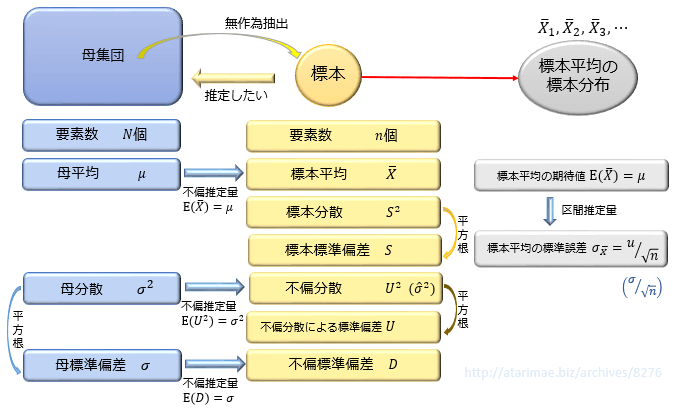
母集団と標本
推測統計学を学ぶうえで、まずおさえておきたいのが「いま母集団と標本どちらの話をしているのか」ということ。
母集団は先の例でいう「日本の成人男性すべての身長データ」。
標本は先の例でいう「無作為抽出して得られた成人男性の身長データ」のことです。
本当は母集団すべてのデータが得られれば一番正確なのですが、それには時間とコストがかかりすぎるため、母集団から無作為抽出された標本のデータを分析することで母集団のデータ(平均・分散・標準偏差)を推定することになります。
統計学で有名なたとえを引用すると
母集団=「鍋に入った味噌汁」
無作為抽出された標本=「よくかき混ぜた後で、小皿にすくった味噌汁」
推定=「小皿の味噌汁を味見して、鍋の味噌汁のあじを推測すること」
と考えると分かりやすいと思います。
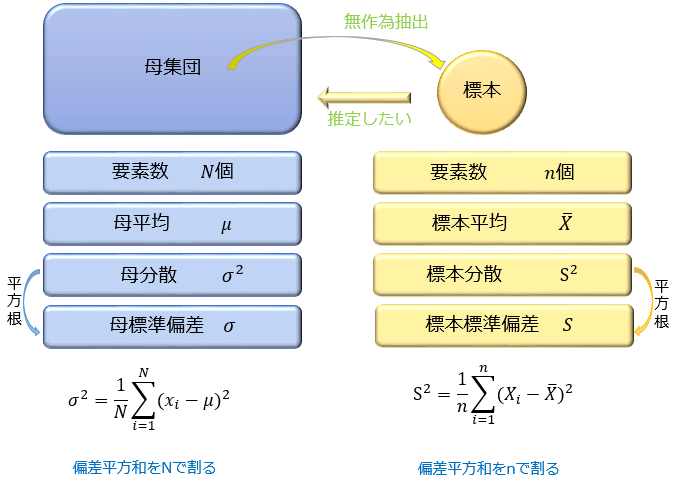
母集団の平均と分散を推定するためには、まず母集団の平均を μ ・分散を σ2 と置くのが一般的です。※母集団の平均は『母平均』・母集団の分散は『母分散』と呼びます。
母集団のデータの値をすべて合計して要素数 N で割った値が母平均。
「母集団の各データの値と母平均の差の2乗の合計(偏差平方和)」を N で割った値が母分散。その平方根が母標準偏差となります。
母集団の各データの値は手元にない(あったら推定する必要がない)ので、母平均や母分散はいったん文字式だけで表されます。
次に、母平均と母分散を推定するための標本データから、標本平均と標本の分散を求めます。
計算方法は母集団と同じで、標本のデータの値を合計して要素数 n で割った値が標本平均。
「標本の各データの値と標本平均の差の2乗の合計(偏差平方和)」を n で割った値が標本の分散。その平方根が標本の標準偏差となります。
標本の各データの値は手元にあるわけですから、標本平均と標本の分散の実現値は(標本平均172cm,標本分散28cm2)といったように具体的な数値として求めることができます。
偏差平方和をnで割ると標本分散。n-1で割ると不偏分散
いま、『偏差平方和を n で割った値が標本の分散』と述べました。
しかし、統計学の教科書のなかには『偏差平方和を n-1 で割った値が標本の分散』と書いてある本もあります。
一見どちらかが間違いのように思うかもしれませんが、実はこれ、「どちらも正しい」です。
これらはどちらも標本の分散であると同時に「使用目的が異なる、別の数値」なんです。
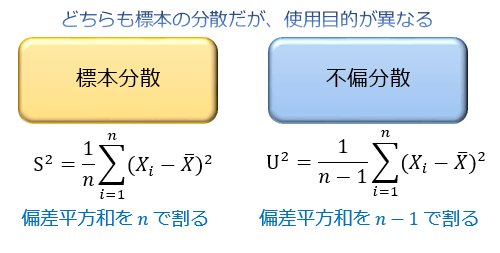
偏差平方和を n で割った値は標本分散(S2)といい、ExcelではVAR.P関数で求められます。
(この標本分散の平方根は、「標本標準偏差」と呼ばれます)
一方、偏差平方和を n-1 で割った値は不偏分散(U2)といい、VAR.S関数で求められます。
(この不偏分散の平方根は、正確には「不偏分散による標準偏差」または「不偏分散平方根」と呼ぶべきですが、単に「標準偏差」と呼ばれることが多いです。この値は母標準偏差の不偏推定量ではないので注意)
①サンプルデータのばらつきの大きさを表す標本分散
標本分散(S2)は先にも述べた通り、母分散を求めるときと同じ計算方法で求められます。
そして、母分散が「母集団のデータのばらつきの大きさを表す」ように、標本分散を使用する目的は「標本のばらつきの大きさを表すこと」にあります。
標本分散は「標本のばらつきの大きさを表す」のには適している一方で、その期待値が母分散と一致しない(過小に評価される)ため、母分散の推定値としてはやや不適切という欠点があります。
これは、出目が(1,2,3)の3つしかないひふみサイコロで考えると分かりやすいです。

②母分散を推定するのに適している不偏分散
『標本分散の期待値 E(S2)』は『母分散』の (n-1)/n 倍になることが分かっています。
それを考慮して、標本分散を n/(n-1) 倍したのが不偏分散です。
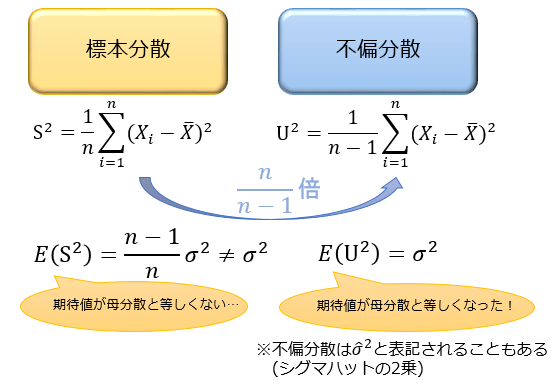
『不偏分散の期待値 E(U2)』は『母分散』と等しくなるので、母分散の推定値として適切な値となります。
このような「期待値が推定したい値と等しい値」のことを不偏推定量と言います。
不偏○○という名前も、不偏推定量であることから由来しています。
先ほどのひふみサイコロの例で言えば、n=2より不偏分散は標本分散の2倍となり、不偏分散の期待値は 1/3×2=2/3 で母分散と等しいことが分かります。
推測統計の文脈では「標本の分散を求めるのは、母分散を推定したいから」が基本であることから、単に『分散』と書いてあったら不偏分散のことを指しているケースが多いことを覚えておきましょう。
(同様に、推測統計の文脈で単に『標準偏差』と書いてあったら不偏分散の平方根を指しているケースが多い)
標本分散:標本のばらつきの大きさを表すときに使う
不偏分散:母集団のばらつきの大きさを推定するときに使う。期待値が母分散に等しい
※サンプルサイズ n が十分に大きいと両者の差はほぼ無くなる
参考文献
まとめに入る前に、今回の参考文献を紹介。
▶学生時代に読んで一番理解が進んだ本。標準誤差・分散分析でつまずいている人にオススメ
▶言葉の省略が少なく、誤解なく勉強が進む。「標本分布」と「度数分布」の違いも分かりやすい
▶膨大なサンプルサイズの難点やt検定時に気を付けるべきことなど、深い内容も
▶「標本分散 s2と標本標準偏差 s」から母集団の推定ができていて、とっつきやすい
▶中学数学までの知識で理解できるように作られており、数式も少なく図表が豊富
▶株や選挙の出口調査など実践的な具体例が豊富で、イメージしやすい
▶大学レベルの内容がキレイにまとまっている
▶コラムや補足コメントの質が高く、復習用教材として重宝する
▶索引が使いやすく、統計用語の定義をド忘れしたときに便利
まとめ
①推測統計学は、母集団から無作為に抽出した標本のデータを調べることで、母集団の性質・特徴を推定する学問。日本の成人男性の平均身長算出や選挙の出口調査など様々な場面で使われている
②推測統計学では分散や標準偏差という言葉が指す対象はたくさんあるので、どの値の話をしているのかキチっと見極める必要がある
③鍋に入った味噌汁が母集団、小皿の味噌汁が標本、味見が推定
④標本の分散には標本分散と不偏分散がある。標本分散は標本データのばらつきの大きさを表すのに使い、不偏分散は母集団のデータのばらつきの大きさを推定するのに使う
⑤推測統計の文脈では、単に『分散』と書いてあったら不偏分散のことを指しているケースが多い(個人的には、不偏分散と明記したほうが良いとは思います)
※用語に混乱があるようで、稀に不偏分散 U2 のことを『標本分散 S2』と表記されていたり、不偏分散による標準偏差 U のことを『標本標準偏差 S 』や『不偏標準偏差』と表記されている教材もありますので、勉強の際は必ずその著者の定義を確認するようにしてください。
なお、今回紹介した参考文献ではいずれもこの記事と同じ用語で統一されています。