金融・政治・社会・経済を語るうえで、大数の法則は欠かすことができません。
銀行が企業にお金を貸せるのも、保険制度が滞らないのも、視聴率を割り出すことができるのも、選挙でまだ開票が終わっていないのに「当選確実」が発表されるのも、すべて大数の法則のうえに成り立っています。
今回は、そんな大数の法則(たいすうのほうそく:Law of Large Numbers)について解説します。
photo credit:tommy@chau
大数の法則とは
まずは、数式的な意味での大数の法則を見ていきましょう。
互いに独立な確率変数 \(X_1,X_2,\cdots,X_n\) が母平均 \(μ\) 母分散 \(σ^2\) の同一の確率分布に従うとき、 その標本平均 \(\overline{X}_{(n)}=\frac{X_1+X_2+\cdots+X_n}{n}\)と任意の正の定数 \(\epsilon\) について
【大数の弱法則】
$$\displaystyle\lim_{n \to \infty}P(|\overline{X}_{(n)}-μ|< \epsilon)=1$$
【大数の強法則】
$$P(\displaystyle\lim_{n \to \infty}\overline{X}_{(n)}=μ)=1$$
が成り立つ。
\(n\) を限りなく大きくすれば、「標本平均 \(\overline{X}_{(n)}\) が母平均 \(μ\) に限りなく近づく確率」は限りなく100%に近づく(確率収束する)というのが弱法則。
\(n\) を限りなく大きくすれば、必ず標本平均 \(\overline{X}_{(n)}\) は母平均 \(μ\) に限りなく近づく(概収束する)というのが強法則です。
いずれにしても、「同一の試行を無限回行えば標本平均は母平均(期待値)に収束する」というのが大数の法則の意味するところです。
たとえば、偏りのないコインを無限回投げれば、表が出た割合は \(1/2\) に限りなく近づき
偏りのないサイコロを無限回投げれば、出た目の平均は \(3.5\) に限りなく近づく
という感じですね。
 By: Anders Eriksson
By: Anders Eriksson具体的にどういうことか?
ただ、ここまではあくまでも「無限回試行したら」という理論的な話です。
実際には無限回試行することはできないので、一般には「現実的に可能な試行回数の範囲内ではどうなるか」に関する以下のような意味で「大数の法則」という言葉が使われています。
【広い意味での大数の法則】
試行回数(サンプルサイズ) \(n\) が大きければ大きいほど、その標本平均 \(\overline{X}_{(n)}\) は極端な値をとる確率が低くなっていき、母平均 \(μ\) に近い値をとる確率が高くなっていく。
例えば、「表が出る確率が \(50%\) のコインを \(n\) 回投げて表が出た割合は \(0.5\) からどのくらい離れた値になるものなのか?」を考えてみましょう。
 By: motoyen
By: motoyen
\(i\) 回目のコイン投げで表が出たら1・裏が出たら0をとる確率変数を \(X_i\) とおきます。
すると、その標本平均 \(\overline{X}_{(n)}=\frac{X_1+X_2+\cdots+X_n}{n}\) はコインを \(n\) 回投げて表が出る割合に一致し、コインを \(n\) 回投げて表が出る割合の母平均は \(μ=0.5\) となります。
これを先ほどの大数の法則に当てはめると、こうなります。
【コイン投げにおける大数の法則】
試行回数 \(n\) が大きければ大きいほど、コインを \(n\) 回投げて表が出る割合 \(\overline{X}_{(n)}\) は \(0.5\) から離れた値をとる確率が低くなっていき、\(0.5\) に近い値をとる確率が高くなっていく。
下の表は、コインを \(n\) 回投げた時の「表が出る割合と母平均の差(絶対値)」の確率の分布です。
一番左上の「\(0.0796\)」というのは「コインを \(n=100\) 回投げた時に、表が出る割合と \(0.5\) の差が \(0\) 以上 \(0.01\) 未満になる確率が \(7.96%\) である」という事を意味しています。

黄色い部分を見比べれば、試行回数を増やしていけば「コインを\(n\)回投げて表が出る割合 \(\overline{X}_{(n)}\) 」が \(0.5\) から離れた値をとる確率が低くなっていくこと
青い部分を見比べれば、試行回数を増やしていけば「コインを\(n\)回投げて表が出る割合 \(\overline{X}_{(n)}\) 」が \(0.5\) に近い値をとる確率が高くなっていくことが分かりますね。
この事実を指しているのが、「大数の法則」です。
収束速度は遅い
大数の法則を扱うときは、1つ注意点があります。
それは、収束速度の遅さです。
先の確率の分布表をもう一度よく読んでみてください。
「コインを \(n=1600\) 回も投げても、表の出る割合と母平均の差が \(0.01\) 以上になる確率がまだ約 \(44%\) もある」ということが分かりますよね。
回数に直せば \(16\) 回以上。モノによっては安易に無視に出来ない差です。
このように、大数の法則はそこまで強い法則ではありません。
大数の法則はすぐに近似できるほど強い収束ではなく、「極端な値を取りにくくなっていく」くらいのふんわりとした収束であるということを覚えておいてください。
これによれば、「確率分布上の母平均との差(ブレ)」を \(1/10\) にするには約 \(100\) 倍の試行回数が必要だと分かります。
大数の法則は、膨大な資金力を持つ銀行や保険会社だからこそ扱える法則と言えるでしょう。
発想の逆転
大数の法則は、それをひっくり返して考えると、また違った重大な事実が見えてきます。
「サンプルサイズが大きければ大きいほど、極端な値をとる確率が低くなっていく」
ということは、裏を返せば
「サンプルサイズが小さい方が、より極端な値をとる確率が高い」
ということでもあります。
これが意味するところは何か?
その答えは、「サンプルサイズに差がある多数のグループをランキング付けしたら、サンプルサイズが小さいグループは極端な上位・下位に食い込む可能性が高い」ということ。
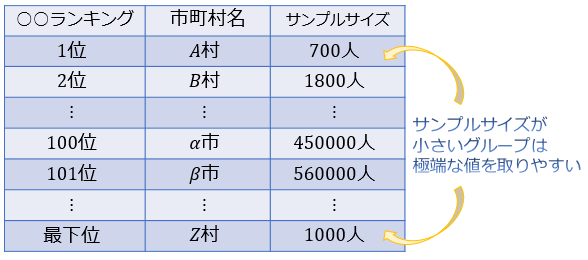
「サンプルサイズが小さいグループは、そもそも潜在的に偏った値を取りやすいにも関わらず、人はそれが偶然によってもたらされたものではなく、何か意味があると錯覚してしまう」というバイアスが存在するんです。
これについては「少数の法則」の記事を参考にしてください。

まとめ
- 大数の法則には数理的には弱法則と強法則がある。いずれにしても「同一の試行を無限回行えば標本平均は母平均(期待値)に収束する」を意味する
- 一般には「試行回数 \(n\) が大きければ大きいほど、その標本平均 \(\overline{X}_{(n)}\) は極端な値をとる確率が低くなっていき、母平均 \(μ\) に近い値をとる確率が高くなっていく」くらいの意味で使われることが多い
- 大数の法則はすぐに近似できるほど強い収束ではなく、「極端な値を取りにくくなっていく」くらいのふんわりとした収束である
- 大数の法則は裏を返せば「サンプルサイズが小さい方が、より極端な値をとる確率が高い」ということでもある。この性質によって差が出ただけのものに対しても、人はそれが偶然によるものではなく、何か意味があると錯覚してしまいやすい
大数の法則や中心極限定理をしっかりと理解したい!という場合は、演習統計学キャンパス・ゼミなどで実際に自分の手で計算してみるのがオススメです。