
「正直者は救われるのか、正直者はバカを見るのか」
世の中には、こういった2択の質問が数多く存在します。
しかし、こういった話の答えは「 0 か 100 か」ではありません。
実際、正直者なおかげで良いこともあれば、正直すぎて損をすることもありますよね。
かと言って、「ケースバイケースだ」という当たり前のことしか言わないのでは、話は一向に進みません。
重要なのは、「答えはどちらなのか」という二者択一的思考ではなく
「正直者は、そうでない人と比べてどの程度良い結果になる確率がそれぞれ何%あり、どの程度悪い結果になる確率がそれぞれ何%あるのか」
「どういうケースでは正直者の方が良い結果につながる確率が高い(or低い)のか」
という確率的思考に他なりません。
この確率的思考をするうえで重要なのが、確率変数(Random Variable)。
確率変数は、世の中の「 0 でも 100 でもない事柄」に対して「25なのか?56なのか?73なのか?」を具体的に考えるのに便利なツールです。
今回は、そんな確率変数について軽く解説していきます。
photo credit:fourbyfourblazer
確率変数とは?
数学では、 x や y といった変数を扱います。
変数は「0以上4以下」といったように値を変化させることができるので、「初速度 2m/s 、加速度 1m/s2 の物体は何秒後に何m先に移動しているか?」といった問題について考えるときに非常に便利な存在です。

しかし、数学で扱う変数は「 x は30%の確率で x=0 になり、70%の確率で x=1 になる」といった使い方はされません。
これに対して、「確率に従っていろいろな値をとる変数」のことを確率変数と言います。
たとえば、「偏りのないコインを2回投げたときに表が出る回数」を X と置いてみましょう。
 By: Waltie
By: Waltie
X は{0,1,2}のいずれかの値をとる変数ですが、ただの変数ではありません。
X は「25%の確率で0」「50%の確率で1」「25%の確率で2」の値をとることから、確率変数となります。
確率変数 X は、X のとる値とその値をとる確率を対応させた表やグラフを書くと分かりやすいです。
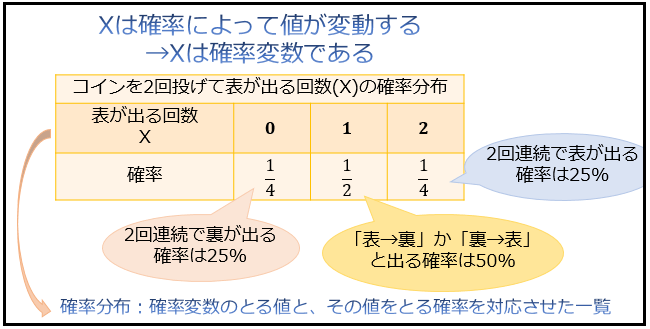
この「確率変数のとる値と、その値をとる確率を対応させた一覧」のことを確率分布と言います。
以上のように確率によって値が変動するものを「確率変数 X」とおき、その確率分布を調べることで、さまざまな物事を「確率による重み」をつけて計算することが可能になるんです。
確率分布を比較する
では、確率変数で「確率による重み」をつけて計算するとどんなメリットがあるのか。
その答えとしては
①リスク・リターンのバランスを考えた選択ができるようになる
②いま起きたことが偶然とは考えにくい現象かどうか判断できるようになる
などが挙げられます。
たとえば
「偏りのないサイコロを投げて出た目の値」= Y
「偏りのないコインを5回投げて表が出た回数+1」= Z
から互いに好きな方を選んで、その数の大きさで勝負するというゲームを考えてみましょう。
(※YかZかを選んでからサイコロ or コインを投げるものとします)
Y も Z も{1,2,3,4,5,6}のいずれかの値をとるという意味では同じですが、「それぞれの値をとる確率」は大きく異なります。
つまり、Y と Z は性質の異なる確率変数なんです。
皆さんなら、Y と Z のどちらでゲームに挑戦しますか?
それぞれの確率分布を見比べて考えてみましょう。
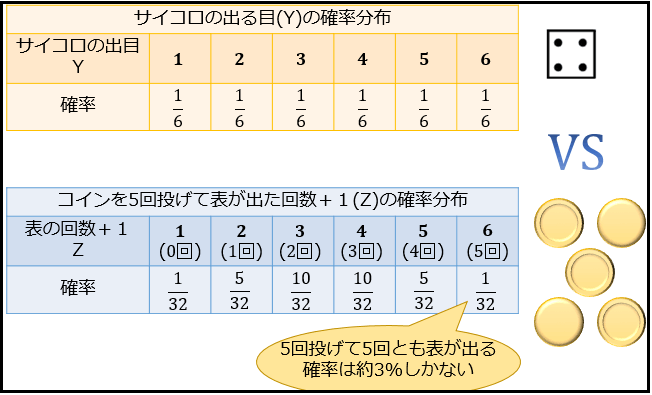
※Zの確率分布の求め方は二項分布の記事を参照。
上の Y と Z の確率分布を見比べてみると、Z のほうが 1 や 6 の値をとる確率が低い=ローリスク・ローリターンな選択であることが分かりますよね。
ここから、手堅く勝負に出たいときは Z を選び、5 や 6 を狙いたいときは Y を選んだ方がいいと判断できるようになるわけです。
また、確率分布から「コインを投げて5回連続表が出る確率は約3%しかない」ことが分かるのもポイント。
約3%の確率なんて、滅多に起きないことですよね。
ここから、相手プレイヤーが1戦目からいきなり5回連続で表を出したり、複数回のゲームに渡って何度も5回連続表を出した場合、「コインに偏りがあるのではないか?」「表が出やすい投げ方をしているのではないか?」と考える事には一定の合理性があることが分かります。
このように、確率分布を知ることで「偶然とは考えにくい現象」かどうかを判断できるようになる。
それが、確率分布を勉強する大きなメリットです。
偶然か否かを判断する知恵
世の中には、さまざまな偶然があります。
「プランAからプランBに変えた途端に売上が上がった」としても、それは偶然の域を出ない差かもしれません。
逆に、「こういうケースでは冷たいお茶よりも温かいお茶を出した時の方が交渉が上手くいくことが多い気がする」と言われたのに対して「そんなの偶然だろ」と思っていても、計算してみたら偶然とは考えにくい差が出ているかもしれません。
偶然を必然と考えたり必然を偶然と考えることによる損失を回避し、チャンスをつかむには、さまざまな確率変数やその確率分布を扱えるようになることが重要です。

多くの統計学の教科書では確率変数や確率分布の説明はサラッとすませていることが多いので、この部分を深く理解したい場合は よくわかる心理統計 や 統計のはなし―基礎・応用・娯楽 などを参考にしながら教科書を読み進めていくのがオススメです。





