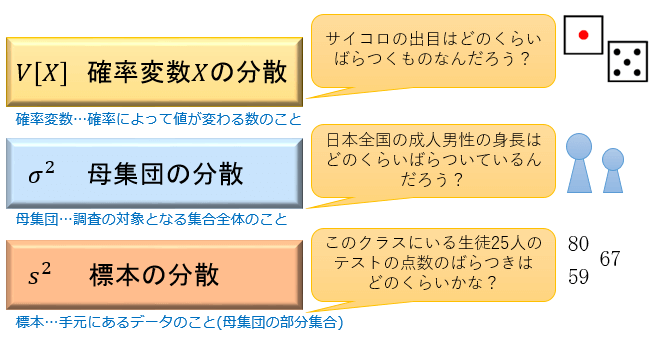
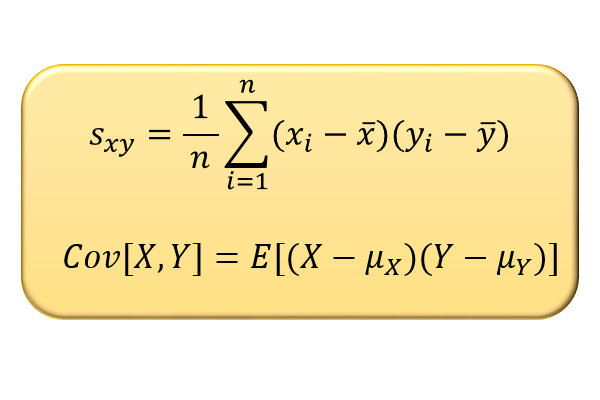重回帰分析とは、複数の説明変数 \(x_1,x_2,\cdots,x_k\) によって目的変数 \(y\) の変動をどの程度説明できるかを分析する手法です。
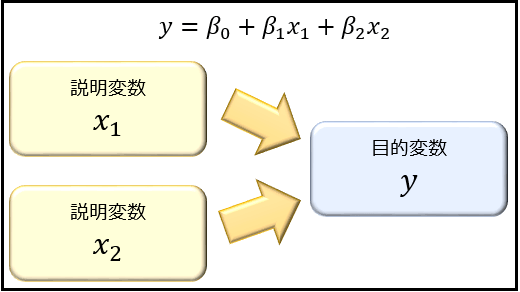
例えば、気温 \(x_1\) と価格 \(x_2\) によって販売量 \(y\) の変動のほとんどを説明できることが分かれば
「明日の気温は \(26\) 度の予報だから、値引き価格の \(180\) 円で販売すると在庫切れになりそうだ。明日は通常価格の \(200\) 円で販売しよう」
といった判断が可能になり、利益の最大化につながります。
このように、重回帰分析は身近にあるさまざまな課題の解決に役立つツールです。道具の1つとして、ぜひ使いこなせるようになっておきたいところ。

そこで今回は、重回帰分析のエクセルでのやり方と結果の解釈の仕方について書いていきます。
エクセルデータ分析の準備
初めてExcelでデータ分析をする場合には、下準備が必要です。
Excel画面左上の「ファイル」⇒「オプション」⇒「アドイン」から「Excelアドイン」の「設定」をクリックしてください。
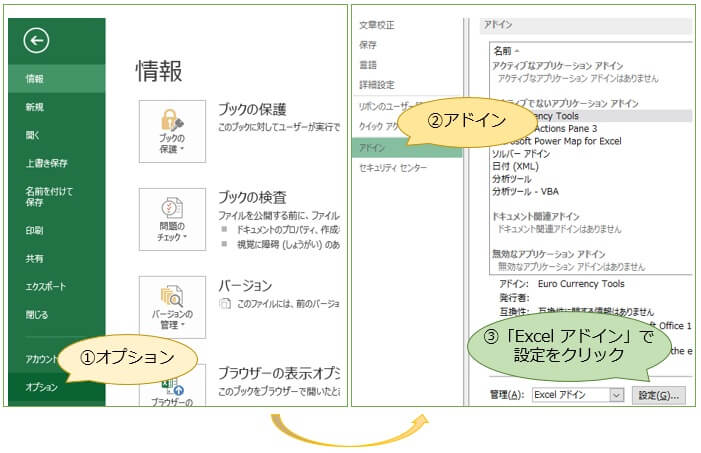
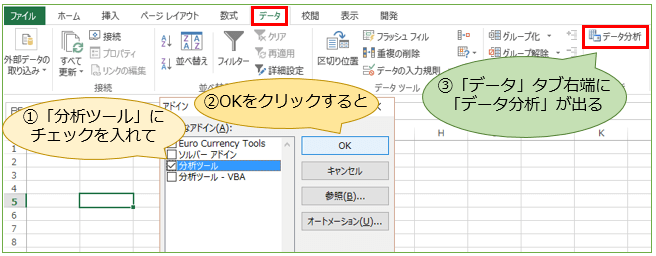
次に、アドインの「分析ツール」にチェックを入れてOKをクリック。
すると「データ」タブの右端に「データ分析」が出てきます。
重回帰分析のやり方
それではさっそく、Excelで重回帰分析をやってみましょう。
一般に、不動産の価格は「部屋が広いほど価格は高くなる」「築年数が長いほど価格は安くなる」「最寄駅までの距離が遠いほど価格は安くなる」と考えられますよね。
では、具体的に「部屋が1m2広い」「築年数が1年長い」「最寄駅までの所要時間が1分多い」ことがどのくらい不動産の価格に影響すると言えるのか?
それを以下の重回帰式を求めることで分析していきます。
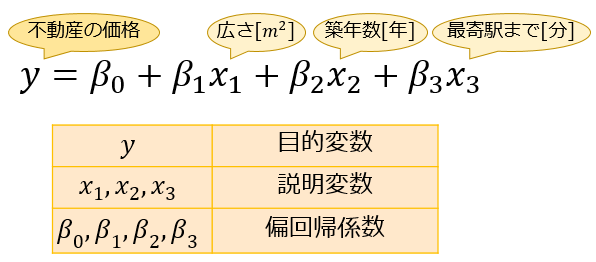
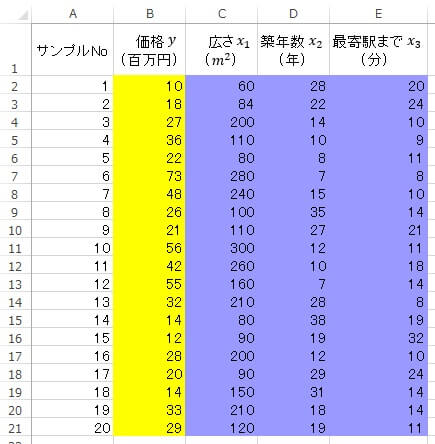
今回使用するデータはこちら。
20個の不動産の価格・広さ・築年数・最寄駅までの所要時間の一覧です。
「データ」タブの「データ分析」から「回帰分析」を選んでOKをクリック。
入力Y範囲に「目的変数となる価格のセル」、入力X範囲に「説明変数となる広さ・築年数・最寄駅までのセル」を入力します。
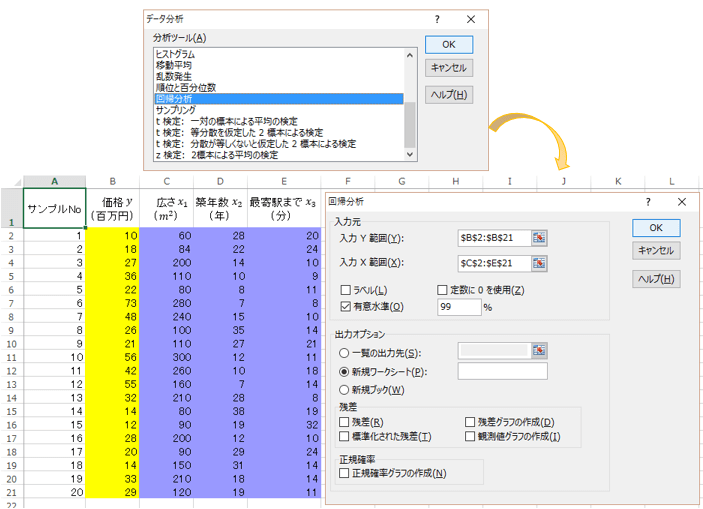
「OK」をクリックすると、重回帰分析の計算結果が表示されます。
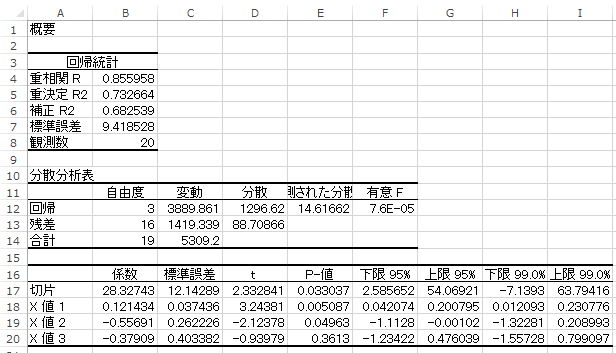
重回帰分析の解釈の仕方
先ほどの結果を見て「たくさん数字が並んでいて読み取るのが大変そう・・・」と思った方もいるかもしれませんが、特に重要なのは以下の黄色で示している部分です。
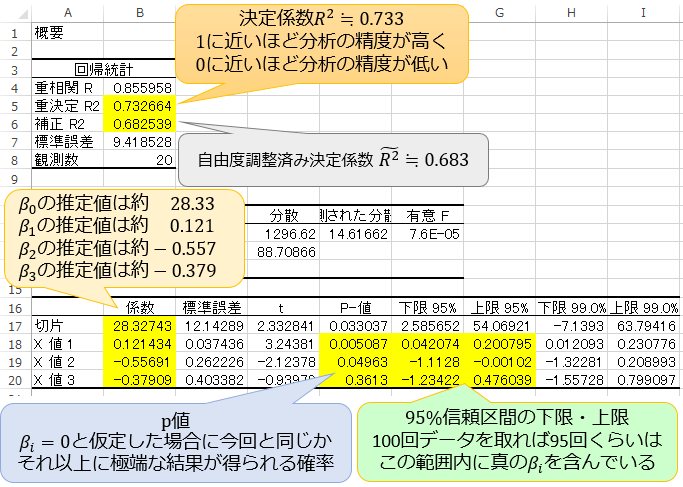
「X値 1」は「 \(x_1\):広さ」、「X値 2」は「 \(x_2\):築年数」、「X値 3」は「 \(x_3\):最寄駅までの所要時間」のことで、係数はそれぞれ偏回帰係数 \(β_0,β_1,β_2,β_3\) の推定値を表しています。
「重決定 R2」は、今回得られた重回帰式の当てはまりの良さを表す指標「決定係数 \(R^2\)」を表しています。
ここから、今回の重回帰分析で得られた重回帰式は以下の通りで、その決定係数は \(R^2=0.733\) と中々当てはまりの良い結果が得られたことが分かります。

決定係数 \(R^2\) は説明変数の個数が増えるほど大きくなってしまう欠点があるので、複数の回帰式を比較する際などには「補正 R2」で表される自由度調整済決定係数 \(\tilde{R}^2=0.683\) を使います。
偏回帰係数は「他の説明変数が一定という仮定の下で、ある説明変数が1だけ変化した時に目的変数がいくつ変化するか」を表す値です。そのため、仮に広さと築年数の相関係数が高い場合にはその仮定が崩れ、不可解な値が得られることもある点に注意が必要です。このように説明変数どうしが強く相関しているせいで解析に支障が出る状態を多重共線性(マルチコ)と言います。
「標準誤差」は「係数 \(β_i (i=0,1,2,3) \) の推定値」がどのくらい「真の \(β_i\) 」からばらつくものなのかを表し、「 t 」は\(「t 値=係数÷標準誤差」\)を表しています。
「P-値」は「\(β_i=0\)と仮定した場合に今回以上に極端な \(t値\) が得られる確率 p値」のこと。
一般にp値が \(0.05\) よりも小さいと「統計的に有意」と言われます。
「\(β_i=0\) の仮定の下では各 \(t値\) が自由度 \(n-k-1\) のt分布に従う」ことを用いて算出されます。(\(n\) はサンプルサイズ、\(k\) は説明変数の数です)
例えば、\(β_1\) のp値は \(0.005\) ⇒もし \(β_1=0\) だとしたら今回のような結果が得られる確率は\(0.5%\)しかない⇒ \(β_1=0\) とは考えにくい⇒「部屋が広ければ広いほど不動産の価格は高くなる」と判断できます。
一方、\(β_3\) のp値は \(0.36\) ⇒もし \(β_3=0\) だとしても今回のような結果が得られる確率は\(36%\)もある⇒ \(β_3=0\) でもおかしくない⇒現時点では「最寄駅までの所要時間が長いほど不動産の価格は安くなる」とは言い切れないと判断できます。
p値については「p値(有意確率)と有意水準を具体例から解説」の記事でさらに詳しく解説しているので参考にしてみてください。
最後に見ておくべきなのが、95%信頼区間。
これは「データを100回取れば95回くらいはこの範囲内に真の \(β_i\) を含む」といえる範囲です。
基本的には「この範囲内に真の \(β_i\) が含まれているのだろう」と考えて分析していくことになります。
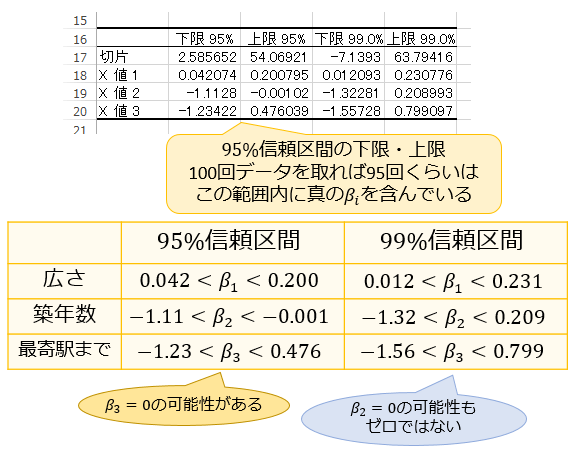
今回の結果からは
部屋の広さは \(0.042<β_1<0.200\) なので「部屋の広さが価格に影響を与えるのは明らかだ」
築年数は \(-1.11<β_2<-0.001\) なので「築年数も価格に影響を与えると考えられるが、もしかしたら \(0\) に近い影響量である可能性もゼロではない」
最寄駅は \(-1.23<β_3<0.476\) で範囲内に \(0\) を含んでいるものの区間の幅が大きいので「最寄駅までの所要時間は価格にほとんど影響を与えない可能性があるが、大きく影響を与えている可能性も否定できないので、もっとサンプルを増やした方が良い」
と判断できますね。