
今回は、回帰分析の主な目的とその種類について解説していきます。
回帰分析とその目的
回帰分析とは、説明変数 \(x\) によって目的変数 \(y\) の変動を \(y=f(x)\) の形でどの程度説明できるかを分析する手法です。
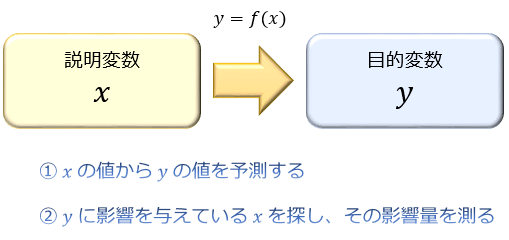
回帰分析を行う主な目的としては、①数値の予測と②要因分析が挙げられます。
①数値の予測

【具体的なストーリー】
ソフトクリームを販売するA社は「仕入れ量の調整」に頭を悩ませています。
ある週は暑くなって販売量が激増し、在庫切れのせいで稼ぐチャンスを逃してしまいました。
またある週は販売量が伸びず、仕入れすぎた在庫を廃棄することになってしまいました。
そこでA社が過去の統計データをもとに回帰分析したところ、「気象データ \(x\) 」によって「ソフトクリームの販売量 \(y\) 」を \(y=f(x)\) の形でほとんど説明できることが分かりました。
この回帰式 \(y=f(x)\) を用いて「天気予報による気象データの予測値 \(x\) 」から「ソフトクリームの販売量 \(y\) 」を予測させてみたところ、95%の確率で誤差±10%以内の予測ができることが判明。仕入れ業務に導入することにより、機会損失リスク・余剰在庫リスクを大幅に減らすことに成功しました。
②要因分析

【具体的なストーリー】
Webショップを運営するB社は「各指標がどのくらい売上に貢献するのか」に関心があります。
「ユーザー数」「1ユーザー当たりのPV」「滞在時間」、どれも伸ばしたいとはいえ、経営資源には限りがあるので「コストと比べて売上貢献度の高い指標」に力をいれたいと考えています。
そこでB社が過去の統計データをもとに回帰分析したところ、最も当てはまりの良い回帰式 \(y=f(x)\) が求まりました。
その回帰式によれば「滞在時間 \(x_1\)」はあまり売上に影響しておらず、「商品購入画面での関連商品のクリック率 \(x_2\)」が大きく売上に影響していることが読み取れます。
そこで、A/Bテストを通じて「商品購入画面での関連商品のクリック率」を高める施策を行ったところ、「ついで買い」が増加。少ないコストで売上を増大させることに成功しました。
ここで注意すべきなのは、回帰分析の結果は飽くまでも判断材料の1つに過ぎないということ。
回帰分析は仮定が正しいという条件のもとでの「最も当てはまりの良い回帰式」を求めているだけなので、本当にその回帰式 \(y=f(x)\) から「数値の予測」や「要因分析」ができるかは人間が判断しなければなりません。
単回帰分析
説明変数 \(x\) が1つだけの回帰式を求めることを、単回帰分析と言います。
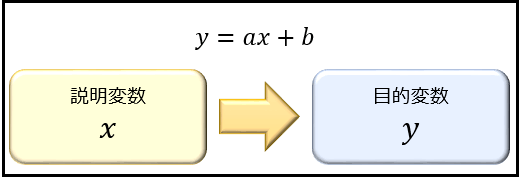
代表的なのが、線形単回帰分析 \(y=ax+b\) です。
単回帰分析は、例えば「気温」と販売量の関係性を調べたい場合に使います。
※「線形」とは、グラフにすると直線になる式であることを意味しています。
重回帰分析
説明変数 \(x\) が2つ以上ある回帰式を求めることを、重回帰分析と言います。
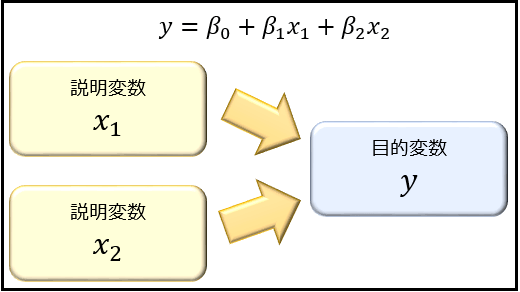
代表的なのが、線形重回帰分析 \(y=β_0+β_1x_1+β_2x_2+\cdots+β_kx_k\) です。
重回帰分析は、例えば「気温と降水量」から販売量の変動を予測・説明したい場合に使います。
※「重回帰分析」の”重”は、「多重」の”重”だと考えると分かりやすいです。
重回帰分析のやり方については「重回帰分析とは。具体例から分かるエクセルでの重回帰分析のやり方とその解釈」を参考にしてみてください。
ロジスティック回帰分析
目的変数 \(y\) が「買った or 買わなかった」のように「 \(0\) か \(1\) のどちらかの値をとる2値変数」である場合、そのまま重回帰分析を行ってもあまり当てはまりの良い結果は得られません。
このような場合に使われるのが、ロジスティック回帰分析です。
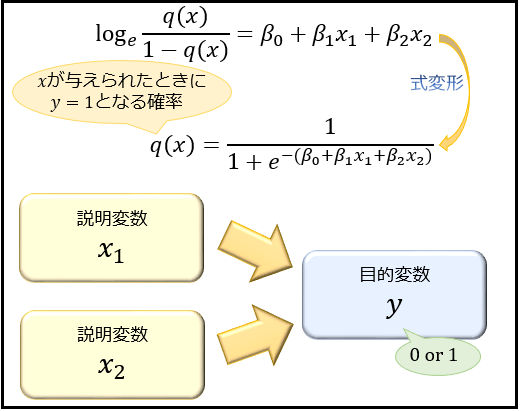
この回帰分析では、「説明変数 \(x\) が与えられたときに目的変数 \(y\) が \(1\) の値をとる確率」を \(q(x)\) とおいて、その対数オッズ \(\log_e \frac{q(x)}{1-q(x)}\) と説明変数 \(x\) の関係性を計算します。
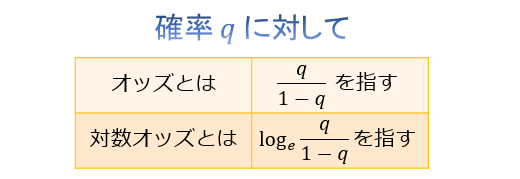
線形重回帰分析では「説明変数 \(x\) が目的変数 \(y\) の値に影響を与える」と仮定されるのに対して
ロジスティック回帰分析では「説明変数 \(x\) が目的変数 \(y=1\) となる確率に影響を与える」と仮定されます。





