統計学の役割の1つに、「それって、たまたまじゃないの?」という疑問に対して「その現象がどれだけ偶然とは考えにくい現象なのか」を論理的に説明する、というものがあります。
(詳しくは「確率変数・確率分布とは何なのか」の記事を参照)
例えば、「サイコロを10回投げた結果、出た目の標本平均が 2 になった」としましょう。
偏りのないサイコロでも、何回か「2以下の目」が出ること自体は珍しくないので、この結果にも「たまたまじゃないの?」という感想を持つ人は少なくないはずです。
しかし、「偏りのないサイコロを10回投げた結果、出た目の標本平均が2以下になる確率」を計算してみると、実は約 \(0.289\) %しかありません。
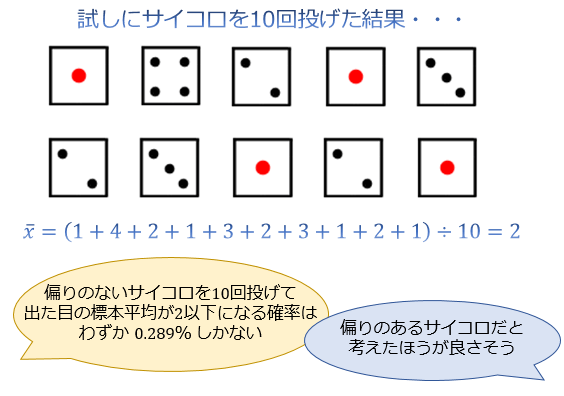
これを踏まえると、「今回たまたま標本平均が小さな値になった」と考えるよりも「偏りのあるサイコロだ」と考えることに一定の合理性があることが分かります。
このように「仮説が正しいとしたら、今回得られた標本平均はどれだけ珍しいものなのか?」を調べることで「たまたまじゃないの?」という疑問を払拭できるのが、統計学の強みです。
ただ、標本平均だけでは、例えば「サイコロを120回投げたら1と6ばかり出た」のに対して「偶然とは考えにくい結果だ」という結論を下すことができません。
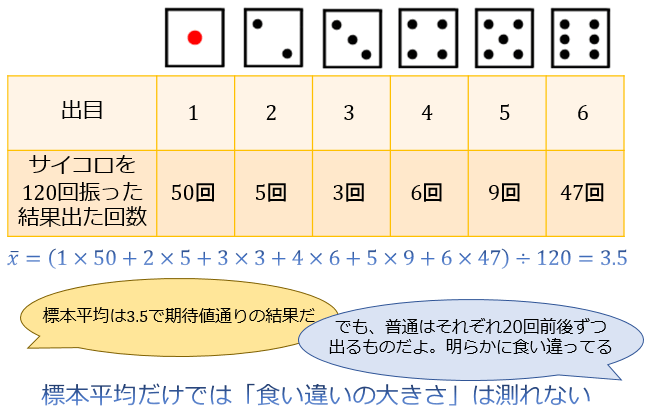
これは明らかに直観に反しますよね。
そこで役に立ってくるのが「理論値からの食い違いの大きさ」について確率的に表した分布。
それが、カイ二乗分布(カイ2乗分布)です。
今回は、このカイ二乗分布の基本的な性質を解説します。
photo credit:Gonzalo Baeza
カイ二乗分布の意味・表記法・確率密度関数を知ろう
カイ二乗分布(\(\chi^2\) 分布)とは、平均が \(0\) で分散が \(1\) の正規分布 \(N(0,1)\) に従う確率変数 \(Z\) を二乗した値である \(Z^2\) をいくつか足し合わせた変数が従う確率分布です。
※\(N(0,1)\)のことを特に標準正規分布と言います。

より正確に言うと、「標準正規分布 \(N(0,1)\) に従う互いに独立な \(n\) 個の確率変数 \(Z_1,Z_2,…,Z_n\) をそれぞれ二乗した値の合計 \(W\) が従う確率分布」のことを、自由度 \(n\) のカイ二乗分布と呼び、\(W\sim\chi^2(n)\) と表記されます。
自由度 \(n\) のカイ二乗分布の確率密度関数は、以下の式で表されます。

正規分布からさらに難解な数式になっていますが、あまり気にしなくて良いです。
自由度1・2・3のグラフと考え方
標準正規分布と自由度 \(1\)・\(2\)・\(3\) のカイ二乗分布をそれぞれグラフで表すと、こんな感じ。
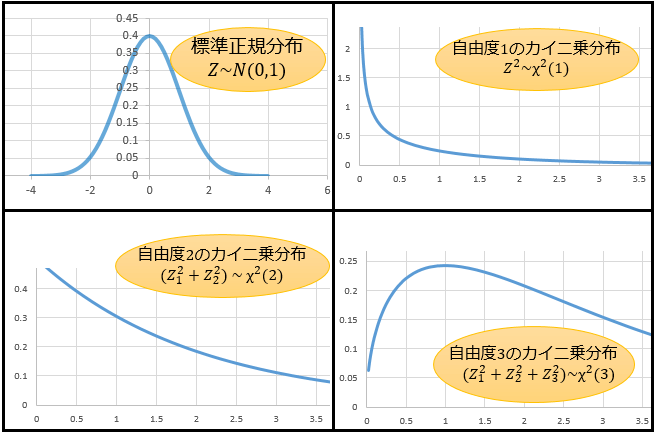
「こういった形の分布をカイ二乗分布と言って、その正確な形を数式で表そうとしたらさっきの確率密度関数になるんだな」くらいに理解しておけば大丈夫。
ポイントとしては、「自由度 \(n\) のカイ二乗分布という存在がどこかにある」と考えるよりも、以下の流れで考えたほうが理解しやすいと思います。
①食い違いの大きさを確率的に考えようとしたら毎回似たような確率分布の話になる
②そのたびに毎回「\(N(0,1)\)に従う互いに独立な〇個の~」と表現するのは手間
③手間を省くために「自由度〇のカイ二乗分布」という名前をつけて一般化した
母平均との差を母標準偏差で割った値の2乗の合計
ここからは、カイ二乗分布と「食い違いの大きさ」について解説していきます。

まず、母平均 \(μ\) 母分散 \(σ^2\) (つまり母標準偏差 \(σ\) )の正規分布に従う \(n\) 個の確率変数 \(X_i\ (i=1,2,…,n)\) を考えます。
「正規分布とは何なのか?その基本的な性質と理解するコツ」の記事で触れた通り、「平均との差は標準偏差何個分か」を表した値である \(n\) 個の \(Z_{i}=(X_{i}-μ)/σ\) は、それぞれ約 \(68.3\) %の確率で「\(-1 \sim +1\)」の値をとり、約 \(95.5\) %の確率で「\(-2 \sim +2\)」の値をとります。
つまり、各 \(Z_{i}\) を二乗した値 \(Z_{i}^2\) は、約 \(68.3\) %の確率で「\(0\) 以上 \(1\) 以下」の値をとり、約 \(27.2\) %の確率で「\(1\) 以上 \(4\) 以下」の値をとり、約 \(4.5\) %の確率で「\(4\) 以上」の値をとることが分かります。
\(Z_{i}^2\) の総和が大きいのは、「母平均からすごく離れた値がある」か「母平均から離れた値が多い」かその両方、つまり「理論値からの食い違いが大きい」ことを意味します。

こう考えると、\(n\) 個の \(Z^{2}_{i}\) を合計した値(総和)は
「\(n=1\) なら大抵 \(4\) 以下、\(n=2\) なら大抵 \(6\) 以下、\(n=3\) なら大抵 \(1\) 以上 \(8\) 以下の値になりそう」という予測が立ちます。
「サイコロを1個投げたら出目は約 \(83\) %(\(5/6\))の確率で \(5\) 以下」
「サイコロを2個投げたら出目の合計は約 \(83\) %(\(30/36\))の確率で \(9\) 以下」
「サイコロを3個投げたら出目の合計は約 \(84\) %(\(181/216\))の確率で \(13\) 以下」
と同じイメージ
この「 \(n\) 個の \(Z^{2}_{i}\) を合計した値」の確率分布こそが、自由度 \(n\) のカイ二乗分布なんです。
普通はこのくらいは自由に動くはず
カイ二乗分布は、ぼく達が経験則として持っている「こういう事をすれば、普通は理論値からこのくらいは食い違った結果になるもの」という感覚を論理的に説明するのに役立ちます。
例えば、サイコロを120回投げたら「すべての目がちょうど20回ずつ出る」という食い違いゼロの結果になることも珍しいですし、冒頭のように「1と6ばかりが出る」という食い違いの大きな結果になることも珍しいですよね。
そのため、「この仮説が正しければ、こんな食い違い方をする確率はこんなにも低い。よって、この仮説は間違っていると考えられる」という検定(カイ二乗検定)をするのに便利な分布となっているんです。
この記事を通じて、「カイ二乗分布の有用性が分かった!」と思っていただけたら嬉しいです。
カイ二乗分布をキチンと勉強したい方には、完全独習 統計学入門という入門書が非常に分かりやすくてオススメです。
次のページでは、カイ二乗分布の代表的な使い方であるカイ二乗検定を見ていきましょう。