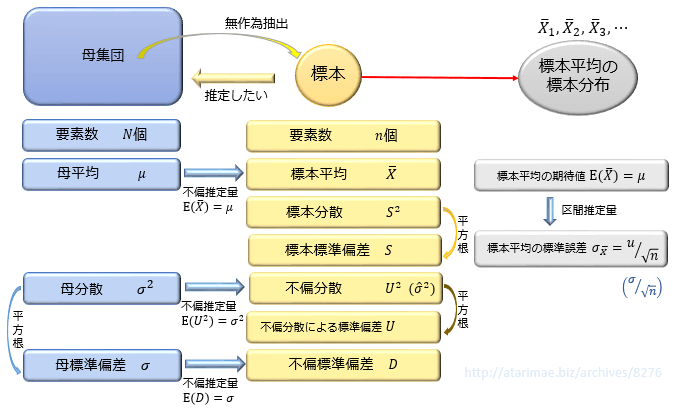
「データのばらつきの大きさ」を調べたいときは、標準偏差を利用するのが一般的です。

しかし、「X社の月間売上高の標準偏差は500万円。Y社の月間売上高の標準偏差は200万円。よって、X社の売上のほうがばらつきが大きい」という評価は必ずしも正しくありません。
仮に、X社の平均売上が1億円なら、ばらつきの小さい安定した経営と言えますし
反対に、Y社の平均売上が250万円なら、ばらつきの大きい不安定な経営と言えるからです。
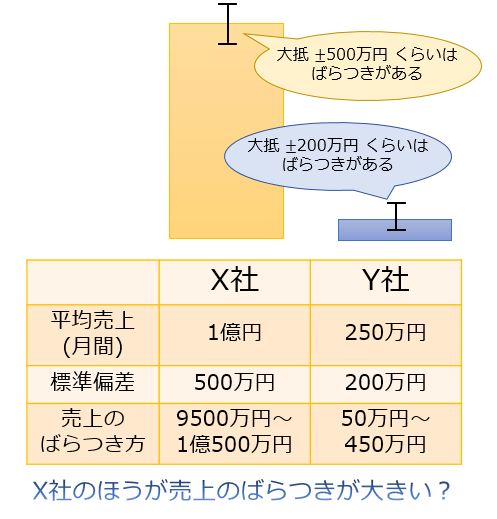
このように、異なるデータ同士のばらつきの大きさを比較したい場合には、数値による「絶対評価」よりも比率による「相対評価」のほうが重要になってきます。
この、異なる種類のデータ同士を比較するときに使う「データのばらつきの大きさの比率」を表したもの。
それが、変動係数です。
photo credit:winnifredxoxo
変動係数の計算方法・公式
変動係数とは「平均に対する、データのばらつきの大きさの比率」を表す指標で、CVと表記される値です。
変動係数は「標準偏差÷平均」という計算式から求められます。

X社の変動係数=500万円÷1億円=0.05
Y社の変動係数=200万円÷250万円=0.8
よってY社の方が売上のばらつきは大きいと言える
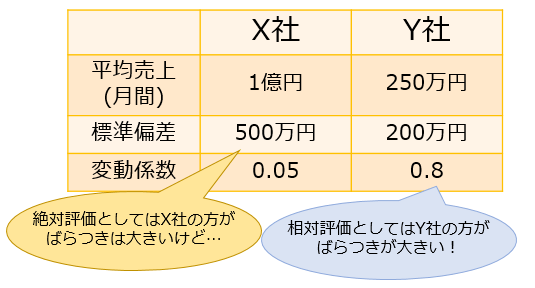
平均売上の単位は「円」・標準偏差の単位も「円」なのに対して、変動係数には単位がないのがポイント。
標準偏差を平均で割ることにより、単位に依存しない指標となり、異なるデータ同士で比較できるようになっているのが変動係数の特徴です。
どの標準偏差を使うべき?
「標準偏差」というと、偏差値の計算などで使う「標本標準偏差 s 」のことを指すことが多いですが、変動係数の計算では「標本標準偏差 s 」を使うべきではないケースが多いです。
標準偏差には「母標準偏差 σ 」「不偏分散平方根 u 」「標本標準偏差 s 」などが存在し、これら3つには以下の特徴があります。
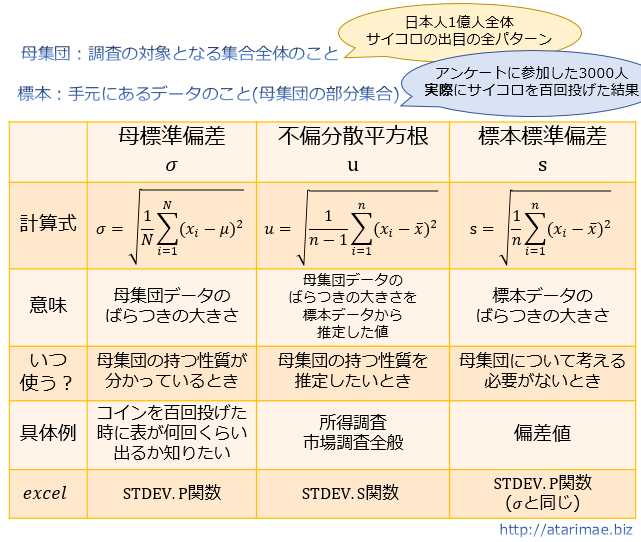
母標準偏差 σ
コインを百回投げた場合、表が出る回数 X は二項分布 B(100,0.5) に従います。
よって、母平均 μ=100×0.5=50、母標準偏差 σ=100×0.5×(1-0.5)=25 であることが分かり、CV=σ÷μ=0.5と求まります。
このように、母集団の持つ性質が分かっているときは、「母標準偏差 σ 」が使えます。
不偏分散平方根 u
多くのビジネス現場や調査において、基本的に σ は未知の値です。
例えば、所得分布の調査では「母集団の持つ性質が不明(日本人の所得分布が不明)」だからこそ調査をするわけですから、「母標準偏差 σ 」は使えません。
このようなケースでは、母標準偏差の推定値である「不偏分散平方根 u 」で代用します。
※不偏分散平方根のことを不偏標準偏差と書いている資料もありますが、不偏分散平方根は「母分散の不偏推定量の平方根」であって「母標準偏差の不偏推定量」ではないので、この表現は誤解を招く表現と言えます。
これについては、日本統計学会公式認定 統計検定2級対応 統計学基礎 p109をご参照ください。
標本標準偏差 s
一方、「標本標準偏差 s 」は偏差値を計算するときのように「母集団の性質はどうでも良く、今回得られた標本データそのものにどの程度ばらつきがあるのかだけに興味がある」場合に使います。
統計書では「n が十分に大きい場合は u と s の大きさには大差がない」・「 s は母標準偏差 σ と計算方法がほぼ同じで理解しやすい」といった理由から、「標本標準偏差 s ÷ 標本平均」が使われていることも多いですが、市場調査等では変動係数は大抵の場合「不偏分散平方根 u ÷ 標本平均」を使った方が良いでしょう。
エクセルで使うとき
エクセルでは「母標準偏差 σ 」および「標本標準偏差 s 」は、STDEV.P関数が対応しています。
一方、「不偏分散平方根 u 」は、STDEV.S関数が対応しています。
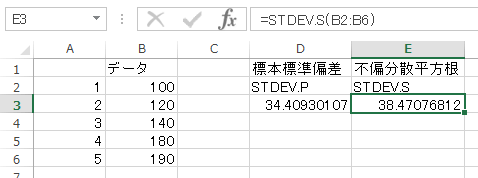
「標本標準偏差 s 」は n で割った値の平方根
「不偏分散平方根 u 」は n-1 で割った値の平方根
なので、不偏分散平方根の方が大きな値になっていることが分かりますね。
「 n で割るか n-1 で割るかの違いの理由」については以下の記事で解説しています。
良ければ、読んでいって下さい。