
今回は、モーメント母関数について書いていきます。
モーメント母関数は、「積率母関数」とも言います。
ただ、「積率母関数」というと確率母関数と文字面が似ているのが難点。
微分・積分のテクニックをたくさん使う論点ではありますが、統計学の地力をつけるためにもぜひマスターしておきたいところです。
photo credit:Nelson L.
モーメント母関数(積率母関数)って何?
モーメント母関数とは、\(m\) 次のモーメント(後述)を生成するための関数です。\((m=1,2,3\cdots)\)
ある確率変数 \(X\) に対して、モーメント母関数 \(M_{X}(t)\) は以下の式で定義されます。

モーメント母関数は、\(e^{tX}\) の期待値として求められる \(t\) の関数です。
\(X\) が従う確率分布によっては「モーメント母関数が存在しない」ケースもありますが、以下のように主要な確率分布の多くにはモーメント母関数が存在します。

※ \(exp(x)=e^x\)
>二項分布
>正規分布
どう使うの?
さて、モーメント母関数を求められると、なにが嬉しいか。
その答えは「モーメント母関数を \(t\) で \(m\) 回微分してから \(t=0\) を代入すると \(m\) 次のモーメントを求められる」ことにあります。
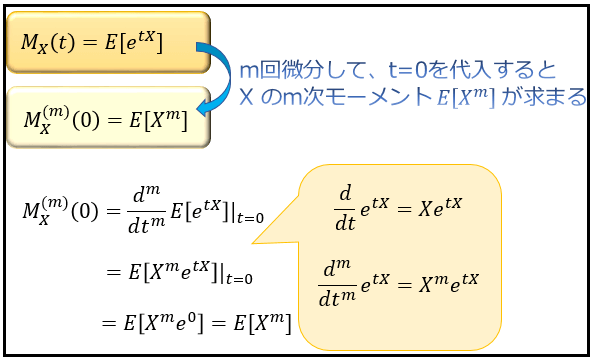
上式のように、モーメント母関数 \(M_{X}(t)\) を \(t\) で \(m\) 回微分してから \(t=0\) を代入すると、\(E[X^m]\) が求められる事が分かります。
この、\(E[X^m]\) のことを \(X\) の原点まわりの \(m\) 次モーメントと言います。\((m=1,2,3\cdots)\)
つまり、\(M_{X}(t)\) を \(t\) で \(1\) 回微分してから \(t=0\) を代入すると「 \(X\) の \(1\) 次モーメント」
\(2\) 回微分してから \(t=0\) を代入すると「 \(X\) の \(2\) 次モーメント」が求まるわけです。
ここから
\(X\) の期待値は「 \(X\) の原点まわりの \(1\) 次モーメント」と等しく
\(X\) の分散は「 \(X\) の原点まわりの \(2\) 次モーメント」から「 \(X\) の原点まわりの \(1\) 次モーメント」の \(2\) 乗を引いた値に等しい
という性質を利用すると…

期待値と分散が求まります。
そう、つまりモーメント母関数さえ分かってしまえば、期待値や分散を求めることができるんです。
そのため、モーメント母関数は「期待値や分散を求める方法の1つ」としても重宝します。
モーメント母関数から期待値と分散を求めてみよう
それでは、具体的にモーメント母関数から期待値と分散を求めてみましょう。
まず、正規分布の期待値・分散を計算してみます。
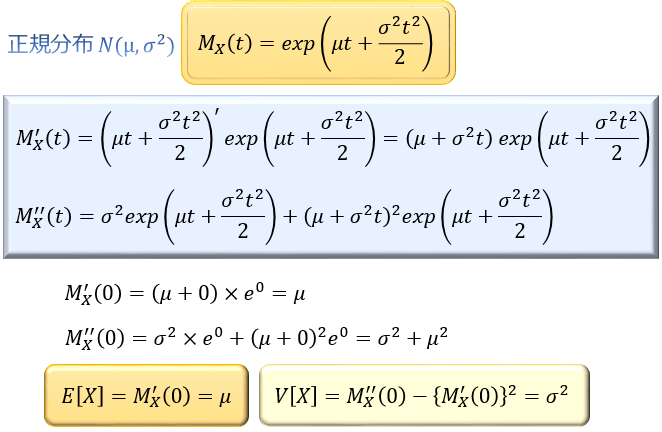
次に、指数分布。
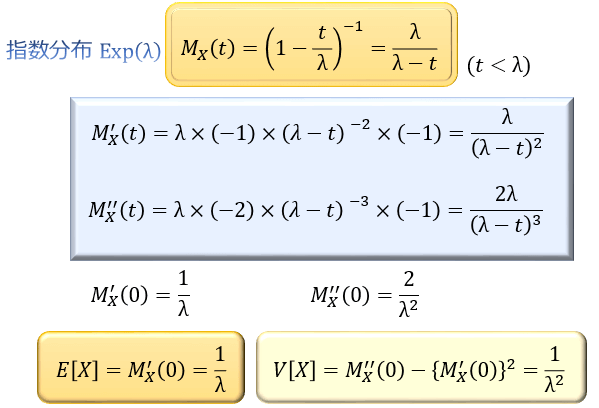
見事、期待値と分散を求めることができました。





