積分とは、「微分の反対」に相当する操作です。
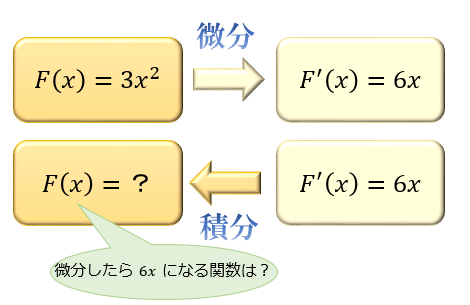
たとえば、\(F(x)=3x^2\) を微分すると \(F'(x)=6x\) になりますよね。
これに対し、積分とは「微分したら \(F'(x)=6x\) になるような \(F(x)\) を求めること」に相当します。
「微分したら \(F'(x)=6x\) になる関数 \(F(x)\)」は、 \(3x^2\) 以外にもたくさんあります。
\(3x^2+4\) や \(3x^2-15\) なども、微分したら \(6x\) になりますよね。
\(3x^2+(定数)\) の形でさえあれば、定数の部分は \(2\) でも \(-1\) でもかまいません。
そこで積分では、これらをまとめて \(F(x)=3x^2+C\)(\(C\) は積分定数)と表記します。

今回は、そんな積分のやり方や「不定積分と定積分の違い」について解説していきます。
積分の記号。インテグラル
関数 \(f(x)\) を積分するときは、\(\int\)(インテグラル)という記号を使って $\displaystyle \int f(x) dx$ と表記します。
\(f(x)\) の左に \(\int\) 、右に \(dx\) をつけることで「関数 \(f(x)\) を \(x\) で積分する」という意味になります。

【豆知識】\(dx\) は「極めて小さな \(x\) の変化量」という意味。
もし \(dx\) を書かなかったら \(\int\) を使った式の答えは大抵 \(+∞\) か \(-∞\) になってしまう。
不定積分と定積分の違い
積分には、不定積分と定積分があります。

これら2つは途中まで同じ計算を行いますが、計算のゴールが変わってきます。
不定積分は「微分したら \(f(x)\) になるような関数を求めること」がゴール
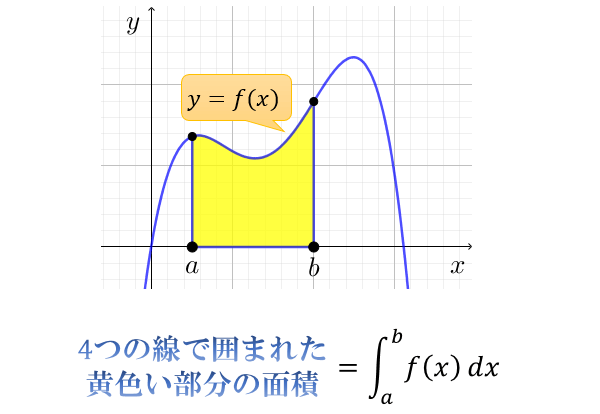
定積分は「関数 \(f(x)\) を \(a\) から \(b\) の範囲で積分し、値の差(面積)を求めること」がゴール
という違いがあります。
それぞれの意味と計算方法を見ていきましょう。
不定積分とは?
「微分したら \(f(x)\) になる関数 $\displaystyle F(x)=\int f(x) dx$ 」のことを、\(f(x)\) の不定積分と言います。
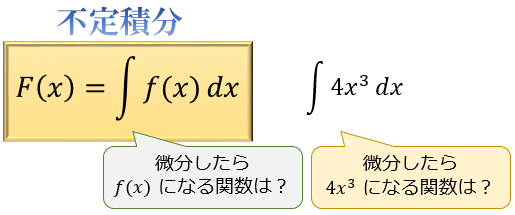
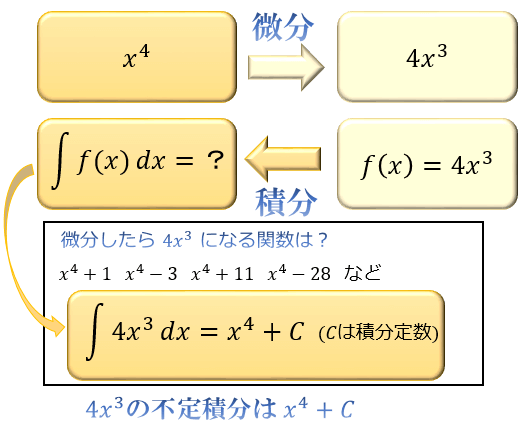
試しに、不定積分 $\displaystyle F(x)=\int 4x^3 dx$ を計算してみましょう。
$\displaystyle F(x)=\int 4x^3 dx$ は「微分したら \(4x^3\) になる関数」を意味します。
「微分したら \(4x^3\) になる関数」としては、\(x^4\) や \(x^4+2\) などがありますよね。
\(x^4+(定数)\) の形でさえあれば定数の部分は \(-3\) でも \(11\) でもかまいません。
これらはまとめて \(x^4+C\)(\(C\) は積分定数)と書けるので
「\(4x^3\) の不定積分は \(x^4+C\) (\(C\) は積分定数)」となります。
定積分とは?
不定積分 $\displaystyle F(x)=\int f(x) dx$ の \(x\) に定数 \(a,b\) を代入して求められた値の差、\(F(b)-F(a)\) を \(f(x)\) の定積分と言います。

不定積分が \(x^4+C\) のような関数であるのに対して
定積分は具体的な値として求まります。
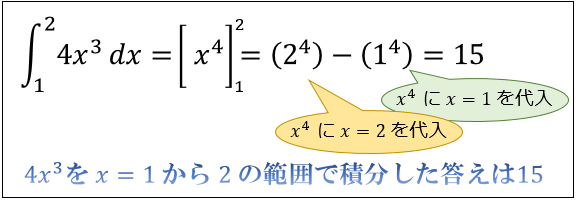
試しに、定積分 $\displaystyle \int_1^2 4x^3 dx$ を計算してみましょう。
$\displaystyle \int_1^2 4x^3 dx$ は「不定積分 $\displaystyle F(x)=\int 4x^3 dx$ に \(x=1,2\) を代入して求められた値の差」を意味します。

不定積分 $\displaystyle F(x)=\int 4x^3 dx$ の答えは \(F(x)=x^4+C\) でした。
この \(F(x)\) に \(x=1,2\) を代入した値の差は \(F(2)-F(1)=2^4-1^4=15\) になります。
これを $\displaystyle \int_1^2 4x^3 dx=15$ と書いて
「\(4x^3\) を \(x=1\) から \(2\) の範囲で積分した答え(定積分)は \(15\) である」と言います。
厳密には \(F(2)-F(1)=(2^4+C)-(1^4+C)\) と書いた方が正確なのですが
定積分は「値の差」を求めるので
\((2^4+C)-(1^4+C)=2^4-1^4\)
となって積分定数 \(C\) が相殺されるため、定積分するときは積分定数 \(C\) は書かなくてOKです。
積分の代表的な公式
ここでは、積分の代表的な公式を紹介します。

\(\sin{x}\) や \(e^x\) などの積分公式については「積分の公式一覧」の記事で紹介しています。

まとめ
- 積分とは、「微分の反対」に相当する操作
- \(f(x)\) の左に \(\int\) 、右に \(dx\) をつけることで「関数 \(f(x)\) を \(x\) で積分する」という意味になる
- 左に \(\int\) を書いたら必ず \(dx\) で閉じる
- 「微分したら \(f(x)\) になる関数 \(F(x)=\int f(x) dx\) 」のことを、\(f(x)\) の不定積分と言う
- 不定積分 \(F(x)\) の \(x\) に定数 \(a,b\) を代入した値の差、\(F(b)-F(a)\) を \(f(x)\) の定積分と言う
- 不定積分は「関数」で、定積分は「値の差(面積)」
- 不定積分は(\(C\) は積分定数)を書く必要があるが、定積分では積分定数 \(C\) は書かなくてOK
次のページでは、「定積分の答えは具体的に何を意味しているのか?」を見ていきましょう。