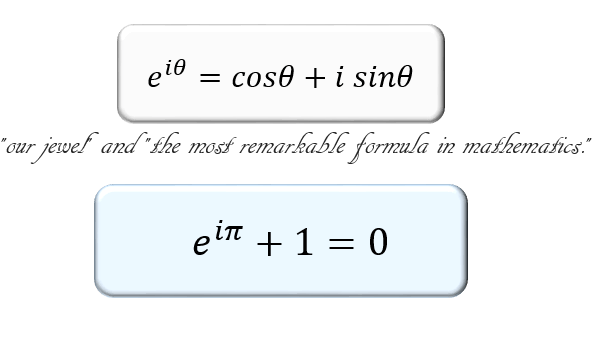勉強しだすと誰もが一度は「わけわからん!!」となる単元。虚数・複素数。
実在しない数をなんで勉強するの?
どうせ将来使わないでしょ?
っていうか結局何のために学ぶの?
こういう感想が出てきてしまいますよね。
そこで今回は、分かりやすさ重視で虚数・複素数とは何なのか、どう役に立ってくるのかについて書いていきます。
photo credit: Karl-Ludwig Poggemann
虚数とは、2乗したら0未満になる数
虚数とは英語で imaginary number といい、2乗したときに0未満の実数になる数を指します。
代表的なのが虚数単位「 \(i\) 」で
\(i×i=-1\)
となります。
英語を直訳すると「想像上の数」 であることからも分かる通り、このような数は現実には存在しません。
複素数とは、実数と虚数を組み合わせたもの
複素数は、皆さんが普段使っている \(1\) や \(3\) といった実数と \(i\) や \(5i\) といった虚数を組み合わせたもの。
「 \(-4+6i\) 」や「 \(5-12i\) 」のように「〇+△\(i\) 」の形で表すことができる数を指します。

実在しないものをなぜ勉強するの?
虚数という言葉を初めて書物に書いたのは、「我思う、故に我あり」で有名なデカルトとされています。
虚数が発見されてから数百年間は「詭弁的な数字であり、実用性はない」「ただの想像上の数に過ぎない」と否定的に評価されていたそうですが、オイラーの等式で有名なレオンハルト・オイラーが虚数のもつ重要性を解き明かした後、その評価は一変。
さらに研究が進むにつれ、その存在を仮定して計算に使ってみたら非常に便利であることが分かり、数学者の間で広く使われるようになったようです。
答え:「虚数が存在すると考えて計算に使うと便利だったから」
どう便利なの?
では、具体的にどう便利なのか?
その答えは、「1つの数で座標を表せること」にあります。
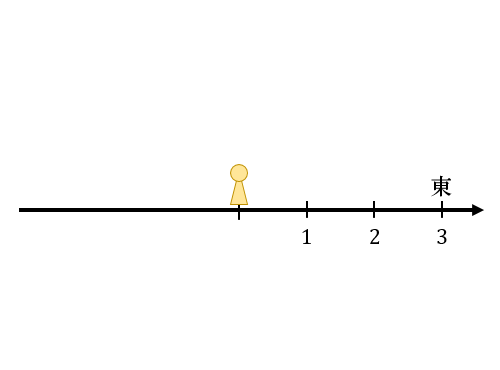
まず、正の数(プラス)しか使えない世界を考えましょう。
この世界では、「東に \(1\) m進む」「北に \(3\) m進む」といった表現しかできません。
そのため「東に〇 m進む」という表現で進める領域は、上図のように東側にしか存在しません。
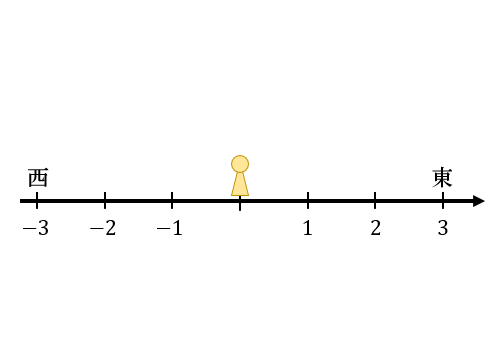
次に、正の数と負の数(マイナス)が使える世界。
この世界では、「西に \(2\) m進む」ことを「東に \(-2\) m進む」と表現することができるようになります。
そのため「東に〇 m進む」という表現で進める領域は、上図のように東西の両側に広がりました。
さて、それでは「東に~」という表現で北や南に進むにはどうすれば良いでしょうか?
少なくとも、正の数・負の数だけでは表現できませんよね。
そこで役に立つのが、虚数です。
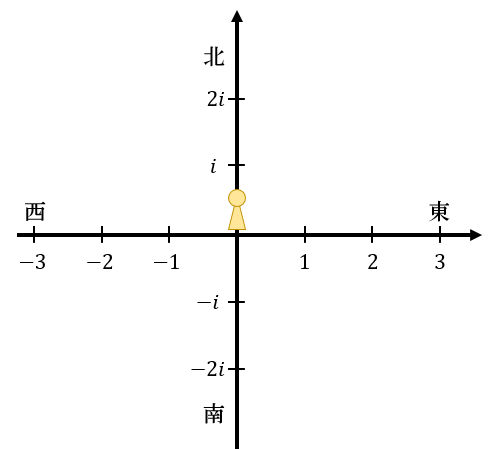
上図が、正の数・負の数・虚数が使える世界。
この世界では、「北に \(2\) m進む」ことを「東に \(2i\) m進む」と表現できるようになります。
「南に \(1\) m進む」のは「東に \(-i\) m進む」と表現できます。
これにより、「東に〇 m進む」という表現で進める領域が東西南北の4方向に広がりました。
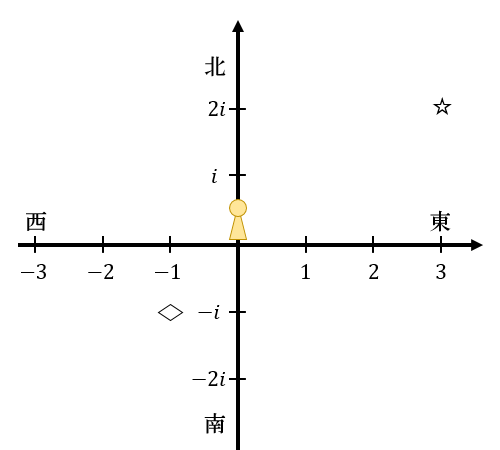
最後に、複素数 (〇+△\(i\) )が使える世界。
この世界では図の星(☆)マークに行くことを「東に \(3+2i\) m進む」と表現できるようになります。
菱形(◇)マークに行くのは「東に \(-1-i\) m進む」と表現できます。
つまり、「東に〇 m進む」という表現だけで平面上の好きな場所へ進めるようになったのです。
このように複素数が使えるようになることで、「東に〇 m進む」という表現で進める領域が4方・8方全ての領域へと広がりました。
これが、1つの数で座標を表せるということです。
(または、複素平面・ガウス平面とも)
南北を i で表現する意味
さて、 \( i\) を利用すれば1つの数で座標を表せることが分かりました。
しかし、なぜ「 \( i\) 」でなければいけないのでしょうか?
「2乗したら \(-1\) になる数」を使う必要性はあるのか?
実は、その必要性があるんです。
その答えは、かけ算にあります。
たとえば \(1+i\) や \(4+2i\) を先ほどの複素数平面で表す場合、下図のように表すことができます。
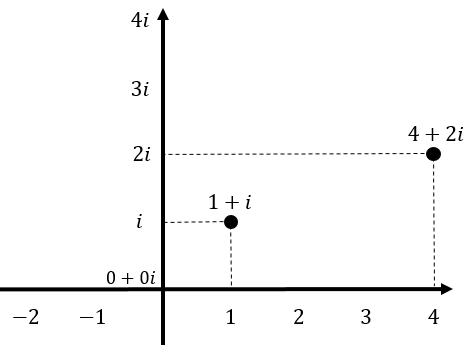
つぎに、 \(1+i\) や \(4+2i\) に \(i\) をかけてみましょう。
\((1+i)× i =-1+i\)
\((4+2i)× i =-2+4i\)
この \(-1+i\) や \(-2+4i\) を複素数平面で表すと、下図のようになります。
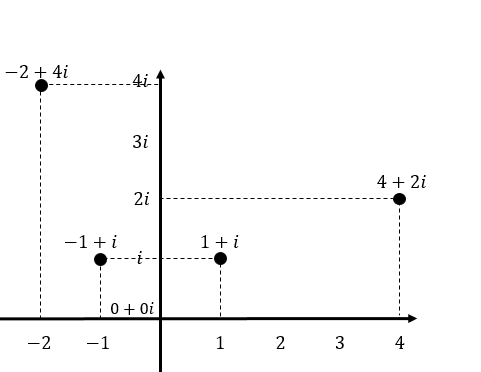
なにかに気づきませんか?
実は、 \(i\) をかけた後の点は \(i\) をかける前の点を「原点を中心に反時計回りに90度回転させた」座標にあるんです。
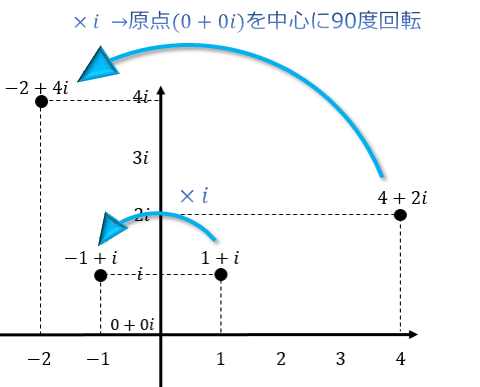
これは \(i\) を何度かけても同じことで、\(i\) を4回かけると
\(i × i × i × i=(-1)×(-1)=1\) で、元の位置に戻ってきます。
ちょうど、90度回転を4回して360度一回転するように。
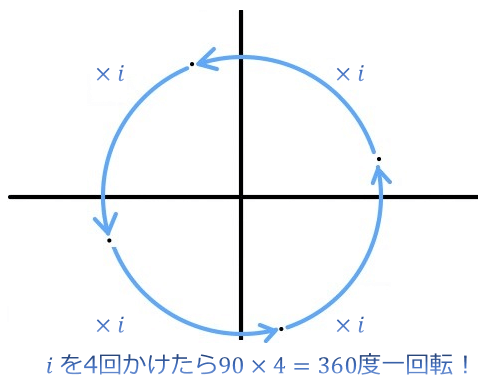
「 \(i\) をかけると反時計回りに90度回転させた座標に移動する」
\(i\) にはこのような性質があるため、「北に \(2\) m進む」ことを「東に \(2i\) m進む」と表現するのにピッタリな存在だったのです。
※「東に \(2i\) m進む」=「東から反時計周りに90度回転させた方向(=北)に向かって \(2\) m進む」
虚数・複素数はこのように、平面上の点の移動を数式でバシッ!と表すことができる、非常に便利なツールとなっているんですよ。
虚数とは「1つの数で座標を表す」のに便利な想像上の数である。
\(i\) をかけることは「原点を中心に反時計回りに90度回転させる」ことを意味する。
虚数について分かりやすく書かれた本としては、Newtonの『虚数がよくわかる』がオススメ。
虚数がどのようにして生まれたのか、どのような領域で役に立っているのか
実在しないはずの虚数が、なぜ自然界に関わって来るのか
などをもっと深く知りたい!という方はぜひ一度読んでみて下さい。