円の面積は、「半径 × 半径 × 3.14」(半径 × 半径 × 円周率 \(π\) )という公式で求めることができます。
例題①半径 \(2\) cmの円の面積を求めて下さい。
答え: \(2 × 2 × 3.14=12.56\)(cm2)
正確には \(2 × 2 × π=4π\)
例題②半径 \(5\) cmの円の面積を求めて下さい。
答え: \(5 × 5 × 3.14=78.5\) (cm2)
正確には \(5 × 5 × π=25π\)
※円周率 \(π\) については「円周の求め方・円周率とは何か・なぜ無限に続くのかを説明。その割り切れない理由について」の記事でくわしく解説しています。
ただ、この公式。「半径 × 半径 × 3.14」が何をどう計算しているのか具体的にイメージしにくいという問題点があります。
「なんでこの公式で円の面積が求まるんだろう?」と感じる方も多いのではないでしょうか。
そこで今回は「なぜ円の面積が半径×半径×3.14になるのか」を見ていきましょう。
photo credit: Travis Wise
円の面積の求め方を図でイメージしてみよう
まず、半径2cmの円を10等分します。
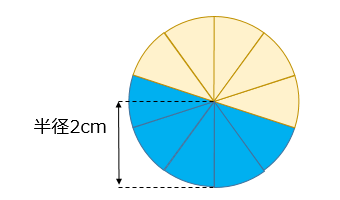
すると、扇の形をした図形が10個できますよね。
この10個の扇形を交互に並べていくと…

下図のような『平行四辺形に近い図形』が出来上がります。
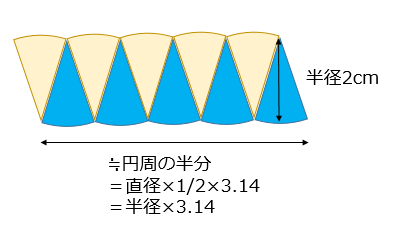
この図形の高さは「半径と同じ2cm」。
横の長さは、およそ「円周の半分=(直径×3.14)÷2=半径×3.14=6.28cm」に近い値となります。
10等分ではまだ上下がデコボコしていますが、円を等分すればするほど平行四辺形に近い形になり、最終的には「高さ=半径」「横の長さ=円周の半分=半径×3.14」の平行四辺形となります。
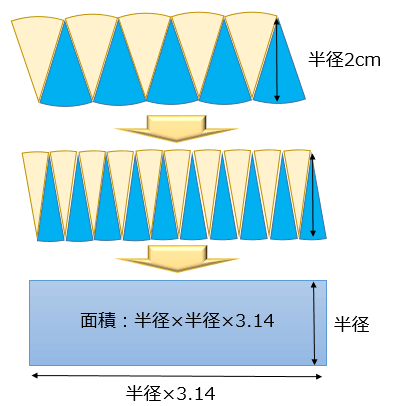
あとは、平行四辺形の面積の公式『高さ』×『横の長さ』を使うと…
円の面積=『高さ』×『横の長さ』=『半径』×『半径×3.14』
みごと、円の面積の公式「半径×半径×3.14」を導き出すことができました。
積分による証明問題
以上の考え方は、「円を無限に細かく分割できること」を前提とした考え方のため、直感的にはイメージできても正確な計算にはなっていません。
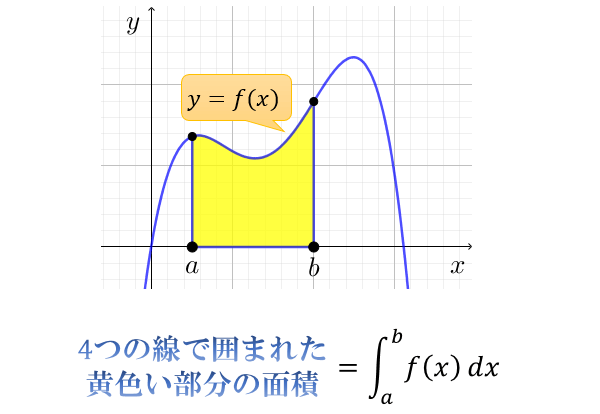
円の面積は、正確には『積分』というテクニックを使うことで以下のように求められます。

積分については、以下の記事で解説しています。