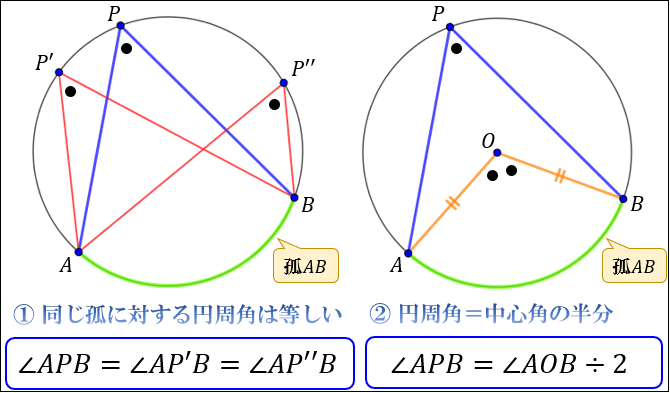
「円の接線 \(AT\) と弦 \(AB\) が作る角 \(∠BAT\) は、弦 \(AB\) に対する円周角 \(∠ACB\) と等しい」という定理を、接弦定理と言います。
接弦定理は、\(∠BAT\) が鋭角・直角・鈍角のどの場合でも成り立ちますが、それぞれ証明の仕方が少しずつ変わってきます。
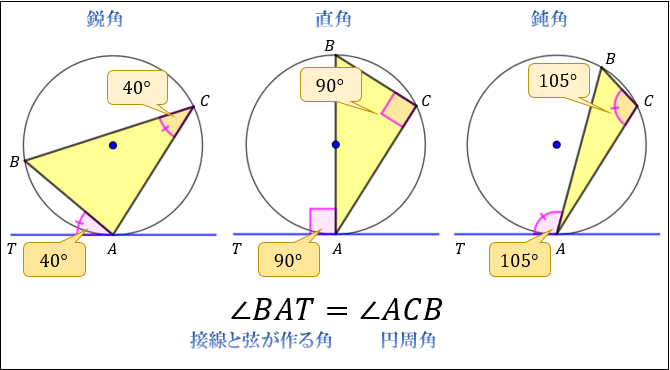
今回は、接弦定理の証明方法を鋭角・直角・鈍角の3つのパターンに分けて見ていきましょう。
① 鋭角のとき(∠BAT < 90°)
初めに、円の接線 \(AT\) と弦 \(AB\) が作る角 \(∠BAT<90°\) のとき。
まず、\(AD\) が円の直径になるように、点 \(D\) をとります。
ここで、三角形 \(ABD\) に注目すると、以下の4つの式が成り立つことが分かります。
● 円周角の定理から \(∠ADB=∠ACB\)
● タレスの定理(直径に対する円周角は直角)から \(∠ABD=90°\)
● \(AT\) は円の接線⇔ \(∠TAD=90°\)(後述) より、\(∠BAT=90°-∠BAD\)
● 三角形の内角の和は \(180°\) より、\(∠BAD=180°-∠ABD-∠ADB\)
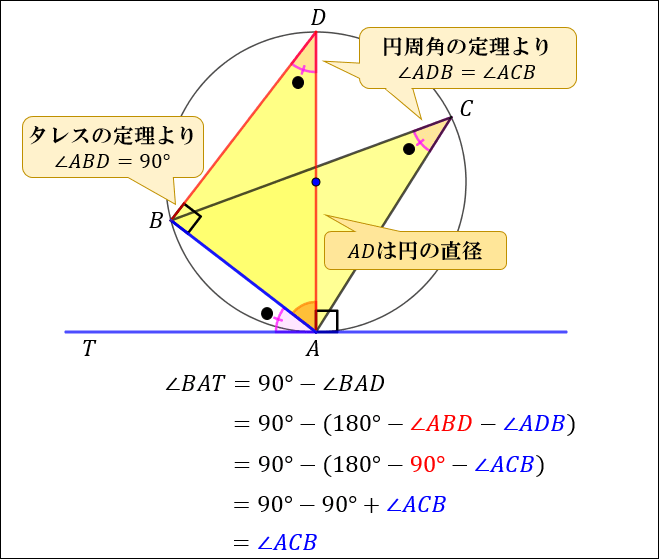
これら4つの式を繋げると
\(∠BAT=∠ACB\) となり、接弦定理を証明できました。
② 直角のとき(∠BAT = 90°)
次は、円の接線 \(AT\) と弦 \(AB\) が作る角 \(∠BAT=90°\) のとき。
三角形 \(ABC\) に注目すると
● タレスの定理(直径に対する円周角は直角)から \(∠ACB=90°\)
● \(AT\) は円の接線⇔ \(∠BAT=90°\)
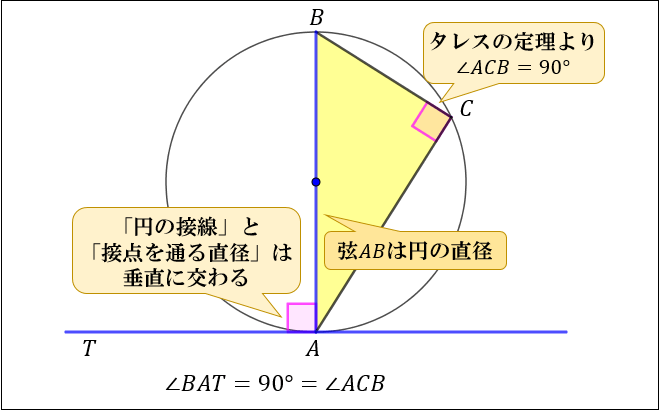
\(∠BAT=∠ACB\) となり、接弦定理を証明できました。
③ 鈍角のとき(∠BAT > 90°)
最後は、円の接線 \(AT\) と弦 \(AB\) が作る角 \(∠BAT>90°\) のとき。
\(T\) とは反対側に点 \(U\) を取ると
弦 \(AC\) について、「① 接弦定理(鋭角)」から \(∠CAU=∠ABC\) が成り立ちます。
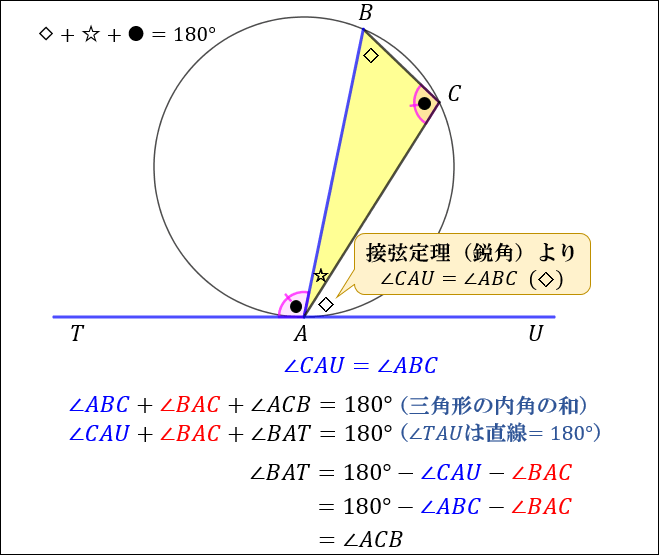
あとは「三角形の内角の和は \(180°\) 」「直線は \(180°\)」を使うと
\(∠BAT=∠ACB\) となり、接弦定理を証明できました。
円の接線が接点を通る直径と垂直になる理由
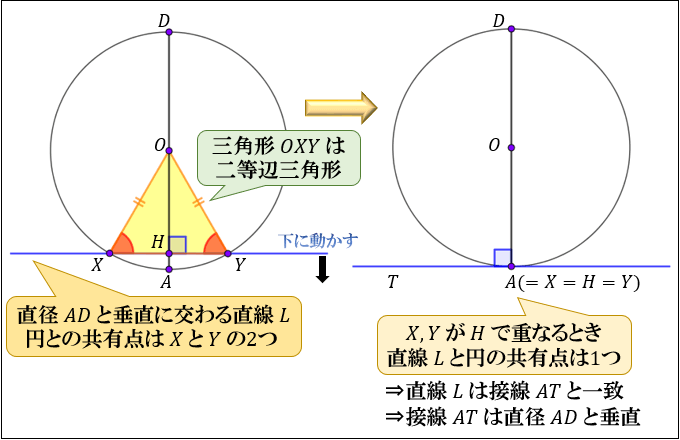
「円の接線 \(AT\) と、接点 \(A\) を通る直径 \(AD\) が垂直に交わる \(∠TAD=90°\) 」ことは、直径 \(AD\) と垂直に交わる直線 \(L\) を少しずつ下にずらしていくことで分かります。
直線 \(L\) と円の共有点を \(X,Y\)、直径 \(AD\) と直線 \(L\) の交点を \(H\) としたら
三角形 \(OXY\) は二等辺三角形になります。
そのため、直線 \(L\) を下にずらしていくと、\(X\) と \(Y\) はどんどん \(H\) に近づいていき、最終的に \(X,Y\) が \(H\) と重なることが分かります。
※共有点:交点,接点などの総称
このとき、「直線 \(L\) と円の共有点」である \(X\) と \(Y\) が重なった
⇒直線 \(L\) と円の共有点が1つになった
⇒直線 \(L\) は円の接線 \(AT\) と一致(接線の定義は円との共有点が1つ)
⇒直線 \(L\) は直径 \(AD\) と垂直に交わる直線
⇒円の接線 \(AT\) は直径 \(AD\) と垂直に交わる
となり、\(∠TAD=90°\) となることが分かります。