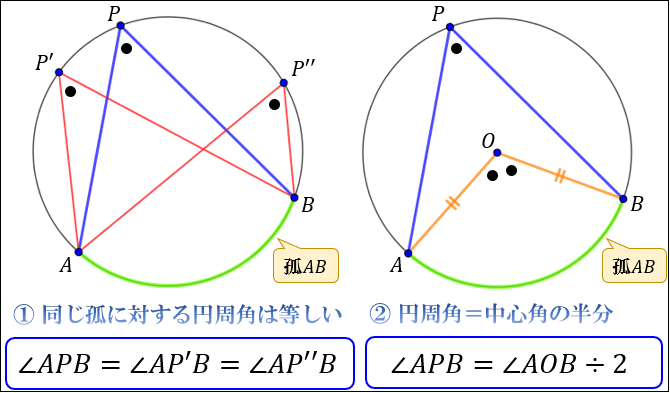
「同じ弧によって作られる円周角の大きさは常に一定」で、「円周角の大きさは同じ弧によって作られる中心角の大きさの半分である」という定理を、円周角の定理と言います。
このページでは、円周角と中心角の意味・円周角の定理・タレスの定理を図を使って解説していきます。
円周角・中心角とは
円の弧 \(AB\) に対して
円周角とは「円周上の点 \(P\) を頂点とする角 \(∠APB\)」のことを言い、
中心角とは「円の中心点 \(O\) を頂点とする角 \(∠AOB\)」のことを言います。
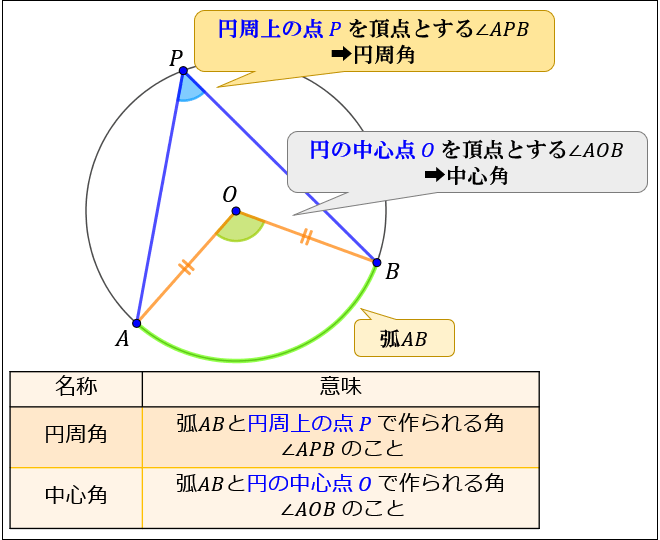
円周角・中心角は、弧に対応して定義されます。
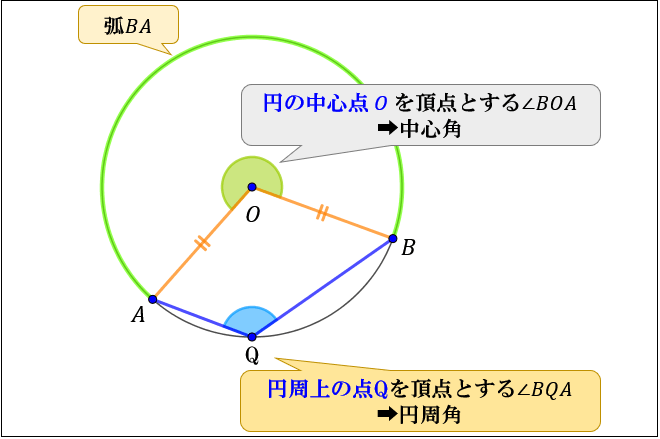
たとえば、反対側の「弧 \(BA\) の円周角・中心角」は、以下のように「弧 \(AB\) の円周角・中心角」とは異なる角度になります。
円周角の定理とは
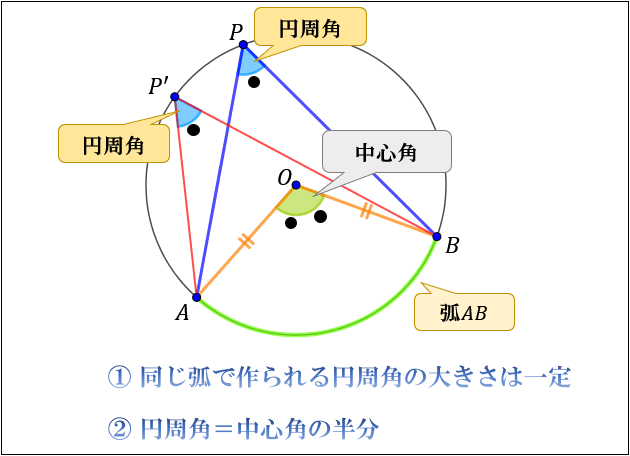
弧 \(AB\) と円周上の点 \(P\) で作られる円周角 \(∠APB\) の大きさは
弧 \(AB\) と円周上の点 \(P’\) で作られる円周角 \(∠AP’B\) と等しく(①)
弧 \(AB\) と円の中心点 \(O\) で作られる中心角 \(∠AOB\) の \(\dfrac{1}{2}\) 倍である(②)
①と②をあわせて、円周角の定理と言います。
①は「同じ弧によって作られる円周角の大きさは、常に一定である」という意味です。
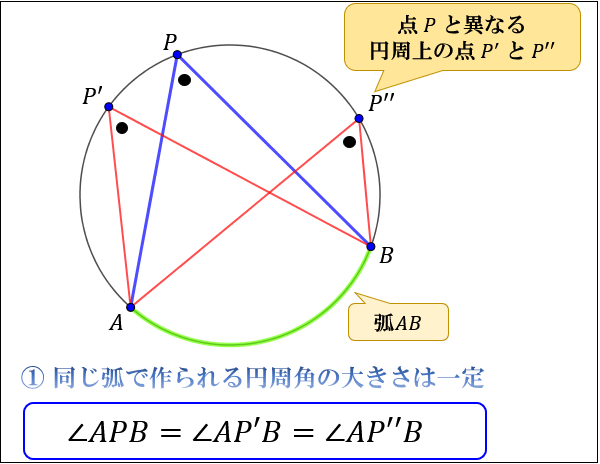
実際に上図の \(∠APB,∠AP^{\prime}B,∠AP^{\prime\prime}B\) を測ってみると
\(∠APB=∠AP^{\prime}B=∠AP^{\prime\prime}B=56°\) で一定であることが分かります。
次に、②は「円周角の大きさは、中心角の大きさの半分である」を意味しています。
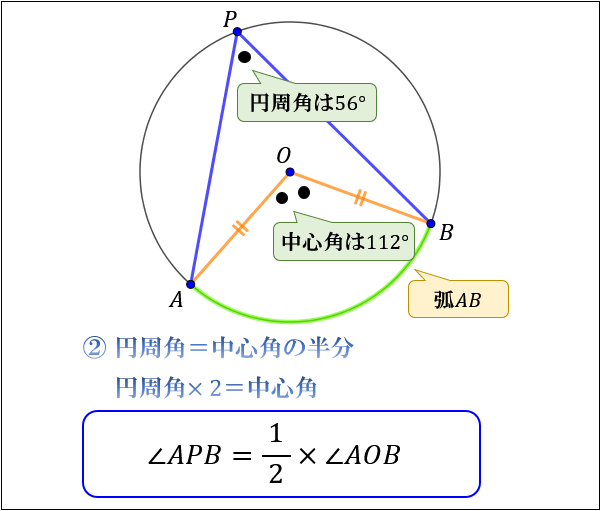
実際に上図の \(∠APB,∠AOB\) を測ってみると
\(∠APB=56°,∠AOB=112°\) で
\(∠APB=\dfrac{1}{2}×∠AOB\) が成り立っていることが分かります。
タレスの定理
【問1】点 \(O\) は円の中心で、点 \(A,O,B\) は一直線上に並んでいます。
このとき、下図の \(∠APB\) を求めて下さい。
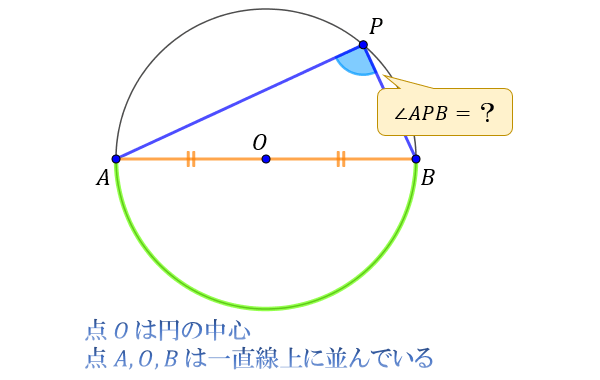
【解答】
\(∠APB\) は「弧 \(AB\) の円周角」です。
そのため、円周角の定理から \(∠APB\) は「弧 \(AB\) の中心角」の \(\dfrac{1}{2}\) 倍だと分かります。
次に、「弧 \(AB\) の中心角」は \(∠AOB\) 。
そしてその角度は、点 \(A,O,B\) が一直線上にあることから、\(∠AOB=180°\)
以上から、\(∠APB=\dfrac{1}{2}×∠AOB=\dfrac{1}{2}×180°=90°\) と求まります。
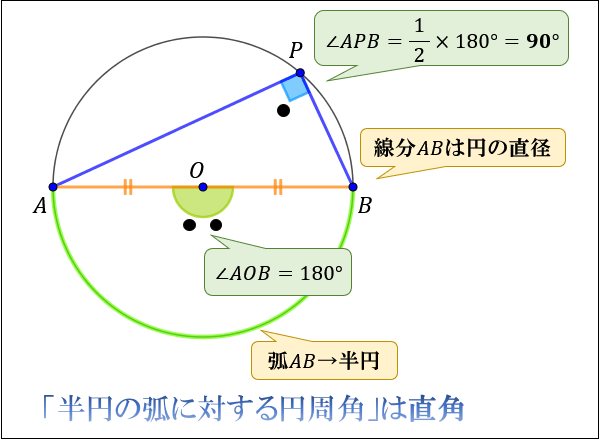
この「半円の弧 \(AB\) に対する円周角 \(∠APB\) は直角になる」という性質はタレスの定理と言って、工学・建築学の世界ではよく使う性質なので、ぜひ覚えておいてください。
【タレスの定理】
線分 \(AB\) を直径とする円の円周上に \(A,B\) と異なる点 \(P\) をとると円周角 \(∠APB\) は直角になる
(言いかえると)半円の弧 \(AB\) に対する円周角 \(∠APB\) は直角になる
円周角の定理を使った問題
【問2】点 \(O\) は円の中心で、点 \(E\) は線分 \(AD\) と \(BC\) の交点です。
\(∠CAD=30°\)、\(∠AEB=100°\) のとき、下図の \(∠ADB\) と \(∠AOB\) を求めて下さい。

【解答】
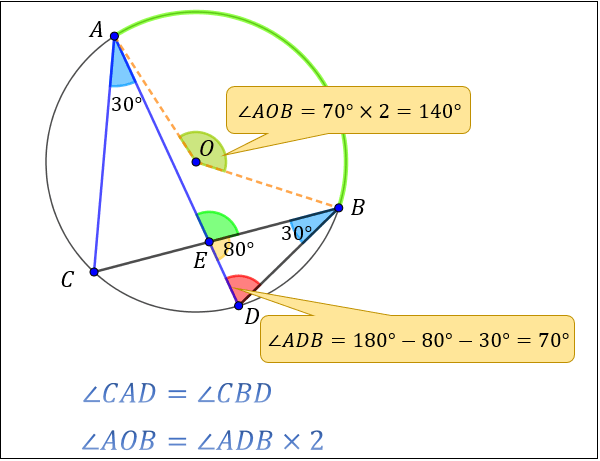
まず、円周角の定理 ① を使って \(∠CBD=∠CAD=30°\) が求まります。
次に、点 \(A,E,D\) は一直線上にあるので、 \(∠BED=180°-∠AEB=80°\)
ここで「三角形の内角の合計は \(180°\)」という性質を使うと、\(∠ADB=180°-30°-80°=70°\) と求まります。
あとは、\(∠ADB\) は「弧 \(AB\) の円周角」・\(∠AOB\) は「弧 \(AB\) の中心角」より
円周角の定理 ② を使って
\(∠ADB=∠AOB ×2=70°×2=140°\) と求まります。
円周角の定理の証明
次のページでは、円周角の定理の証明を見ていきましょう。