円周角の定理の証明。3つのパターンから分かる円周角と中心角の関係性

 

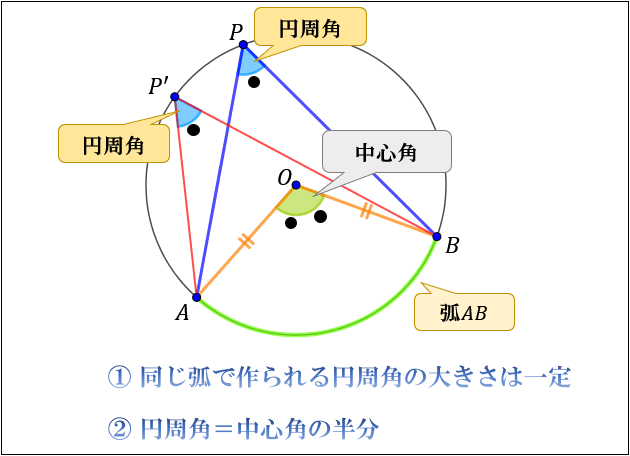
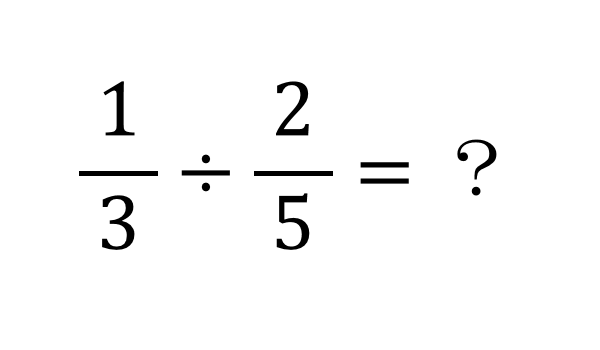「同じ弧\(AB\) に対する円周角 \(∠APB,∠AP^{\prime}B\) は等しく、同じ弧に対する中心角 \(∠AOB\) の半分である」という定理を、円周角の定理と言います。

 

円周角の定理の証明には

の3つのパターンの証明が必要です。

 

このページでは、円周角の定理の証明方法を3つのパターンに分けて見ていきましょう。

 

①「円周角の内側」に円の中心がある

まずは、「円周角 \(∠APB\) の内側」に円の中心 \(O\) がある場合。

 

\(OA=OP\)（円の半径）から、三角形 \(OAP\) は二等辺三角形

\(OB=OP\)（円の半径）から、三角形 \(OBP\) も二等辺三角形

という性質を利用します。

 

 

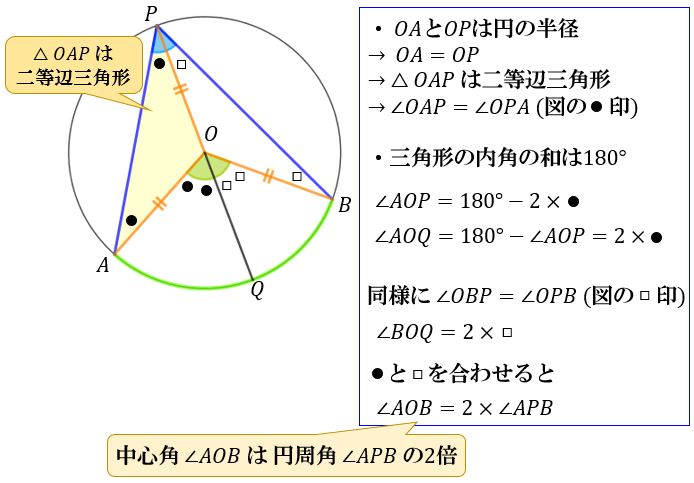
円周角が \(∠APB=●+□\)

中心角が \(∠AOB=2×(●+□)\) 

なので、「円周角が中心角の半分である」ことを示せました。

 

②「円周角の線分上」に円の中心がある

次は、「円周角 \(∠APB\) を作る線分 \(PB\) 上」に円の中心 \(O\) がある場合。

（線分 \(PA\) 上に円の中心 \(O\) がある場合も同様）

 

 

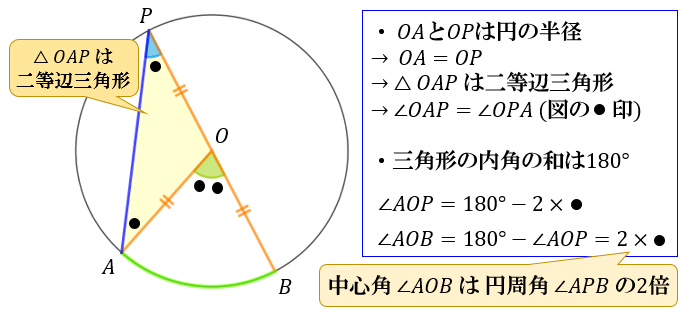
円周角が \(∠APB=∠APO=●\)

中心角が \(∠AOB=2×●\) 

なので、「円周角が中心角の半分である」ことを示せました。

 

③「円周角の外側」に円の中心がある

最後は、「円周角 \(∠APB\) の外側」に円の中心 \(O\) がある場合。

 

点 \(P\) から、円の中心 \(O\) を通る補助線 \(PQ\) を引くのがポイントです。

 

 

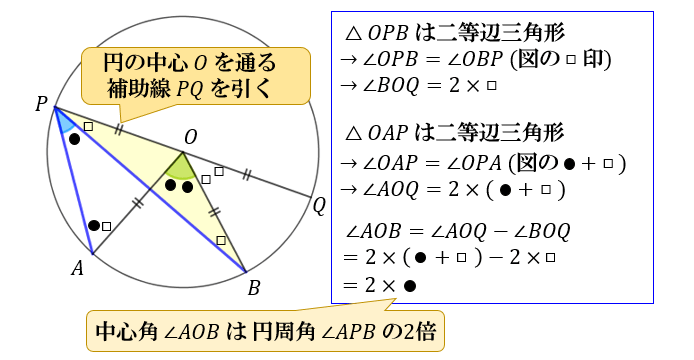
線分 \(PQ\) は円の中心 \(O\) を通るので、「② 円周角の線分上に円の中心がある」のパターンを使うと

\(∠BOQ=2×∠BPQ=2×□\)

\(∠AOQ=2×∠APQ=2×(●+□)\)

が分かります。

 

あとは、この2つの差をとると

円周角が \(∠APB=●\)

中心角が \(∠AOB=2×●\) 

となり、「円周角が中心角の半分である」ことを示せました。