今回は、有理数と無理数について。
有理数は英語で Rational Number 、無理数は英語で Irrational Number と言います。
「Ratio=比」という意味からも分かる通り、有理数とは整数の比で表される数という意味です。
この記事では、有理数と無理数の違いを見ていきましょう。
有理数か無理数か。その判別法
\(a\) , \(b\) を整数としたとき
● 「2つの整数 \(a\) , \(b\) を使って \(\dfrac{a}{b}\) と表せる数」のことを有理数
● 「2つの整数 \(a\) , \(b\) を使って \(\dfrac{a}{b}\) と表すことができない数」のことを無理数
と言います。 \((b≠0)\)
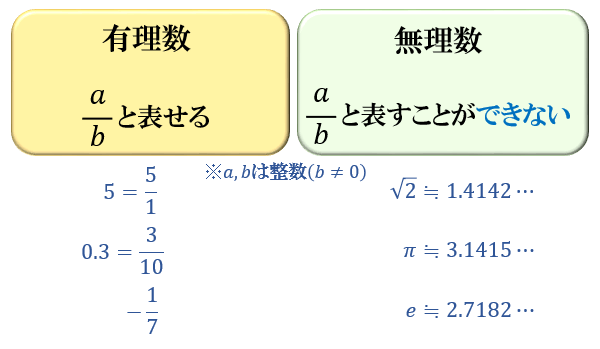
たとえば、\(5\) や \(0.3\) や \(-\dfrac{1}{7}\) などはすべて有理数です。
これらは \(5=\dfrac{5}{1}\) 、 \(0.3=\dfrac{3}{10}\) 、 \(\dfrac{-1}{7}\) のように
整数 \(a\) , \(b\) を使って \(\dfrac{a}{b}\) の形で表せていますよね。
反対に、どう頑張っても \(\dfrac{a}{b}\) の形で表せない数があれば、その数は無理数と呼ばれます。
有理数の定義:「整数の比で表される数」
無理数の定義:「有理数でない実数」
有理数に含まれるもの
有理数は大きく分けて、以下の3種類に分けることができます。
- 整数
- 有限小数
- 循環小数
上から順番に見ていきましょう。
整数
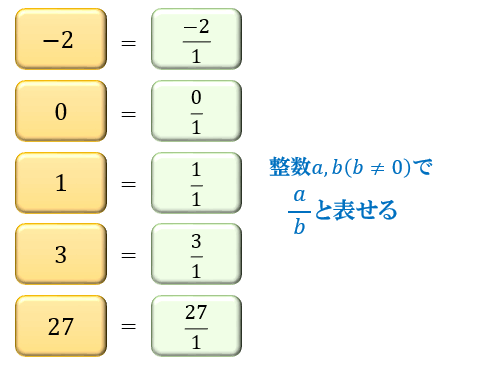
まず、整数はすべて有理数に含まれます。
例えば \(1=\dfrac{1}{1}\) や \(3=\dfrac{3}{1}\) といったように、すべての整数は「整数 \(a,b\) を使って \(\dfrac{a}{b}\) と表すことができる」からです。
有限小数
次に、有限小数。
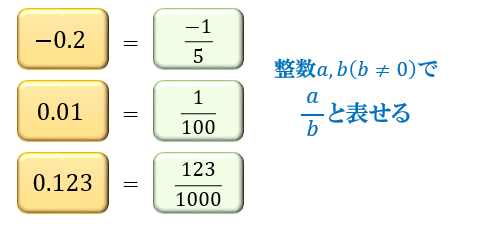
有限小数とは、\(0.3\) のように「小数点以下の値が無限には続かない」数のことです。
有限小数も、すべて有理数に含まれます。
これは例えば \(0.123=\dfrac{123}{1000}\) といったように、桁が有限の小数なら必ず整数 \(a,b\) を使って \(\dfrac{a}{b}\) と表すことができるからです。
循環小数
最後に、循環小数。
循環小数とは、\(\dfrac{1}{3}=0.333\cdots\) のように小数点以下の値が無限に続くけれども、その数字がループしている小数のことです。
循環小数も、すべて有理数に含まれます。
これを整数の比で表すには、例えば \(0.2525\cdots\) のように \(25\) がループしている循環小数なら、まず \(S=0.2525\cdots\) とおくのがコツ。
次にそれを \(100\) 倍した \(100S=25.25\cdots\) から \(S\) を引くと、 \(99S=25\) ⇔ \(S=\dfrac{25}{99}\) となり、整数の比で表せるのが分かりますね。

ルート2が無理数である証明
ここまでは「2つの整数 \(a\) , \(b\) を使って \(\dfrac{a}{b}\) と表せる数」である有理数を見てきました。
その反対で「2つの整数 \(a\) , \(b\) を使って \(\dfrac{a}{b}\) と表すことができない数」が、無理数です。
代表的な無理数としては、\(2\) の正の平方根 \(\sqrt{2}≒1.414\) が挙げられます。
\(\sqrt{2}\) とは、\(\sqrt{2}×\sqrt{2}=2\) となるような数のことで、ルート2と読みます。
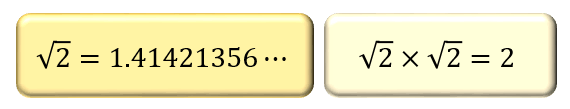
詳しくは「平方根√とは何か。計算方法・覚え方・どう役に立つのかを解説」の記事を参考にしてください。
\(\sqrt{2}\) は \(1.41421356\cdots\) と小数点以下の値に規則性がなく、いかにも「2つの整数 \(a\) , \(b\) を使って \(\dfrac{a}{b}\) と表すことができない」感じがしますよね。
実際、以下のように背理法を使うことで、\(\sqrt{2}\) が「2つの整数 \(a\) , \(b\) を使って \(\dfrac{a}{b}\) と表すことができない」ことを証明することができます。