\(\sqrt{2}=1.41421356\cdots\) は「一夜一夜に人見頃」と覚えます。
これは「一晩経つごとに桜の花が開いていき、見頃に近づいていく様子」を表す語呂合わせです。
この記事では、こういった平方根の語呂合わせをまとめました。
ルート23のような「大きな素数の平方根」の筆算のやり方も解説してきます。
ルート2
\(\sqrt{2}=1.41421356\cdots\)
一夜一夜に人見頃(ひとよひとよにひとみごろ)
一晩経つごとに桜が満開に近づいていく様子
ルート3
\(\sqrt{3}=1.7320508\cdots\)
人並みに奢れや(ひとなみにおごれや)
非常に完成度の高い語呂
ルート5
\(\sqrt{5}=2.2360679\cdots\)
富士山麓オウム鳴く(ふじさんろくおーむなく)
ルート2・ルート3・ルート5の3つはぜひ覚えておきましょう
ルート6
\(\sqrt{6}=2.4494897\cdots\)
煮よ、よく、弱くな(によよくよわくな)
弱火でじっくり煮るイメージ
ルート7
\(\sqrt{7}=2.6457513\cdots\)
浮浪、死後、何個遺産(ふろうしごなんこいさん)
\(7→2.64575\) で「菜に虫いない」が有名。\(5=\) 「い」は苦しいですがイメージはしやすいです
ルート8
\(\sqrt{8}=2.828427\cdots\)
庭には呼ぶな(にわにはよぶな)
\(\sqrt{2}\) の \(2\) 倍
ルート10
\(\sqrt{10}=3.162277\cdots\)
\(\sqrt{10}≒3.1623\) で父さんイチロー兄さん(とお さんいちろーにーさん)
\(3.162277\) で「三色に並ぶ」(\(2\)と\(7\) が並んでいる)も有名
大きな値の平方根の筆算の仕方
大きな値の平方根の求めるときは、電卓やEXCEL(SQRT関数)を使うのが一番ですが、試験中や紙とペンしかないときは筆算で求めるしかありません。
ルート15の場合
例えば、\(15=3×5\) のように簡単な素数のかけ算に直せる値の平方根なら
\(\sqrt{15}=\sqrt{3}×\sqrt{5}\) \(≒1.732×2.236≒3.873\)
といったように求めます。
ルート23の場合
\(\sqrt{23}\) のように、簡単な素数のかけ算に直せない値の平方根の場合は、以下の手順を踏みます。
Step① \(2\) 乗した値が \(23\) 以下となる最大の整数 \(n\) を考える \((n=4)\)
Step② \(n\) を筆算の上に1個、左に2個並べて書く(2個目に+をつける)
Step③ \(23\) から \(n^2=16\) を引き、\(100\) 倍する
Step④ その左に、上の値 \((4+4)\) の合計と空欄を1つ書く (\(80\) 以上 \(89\) 以下の値を意味する)
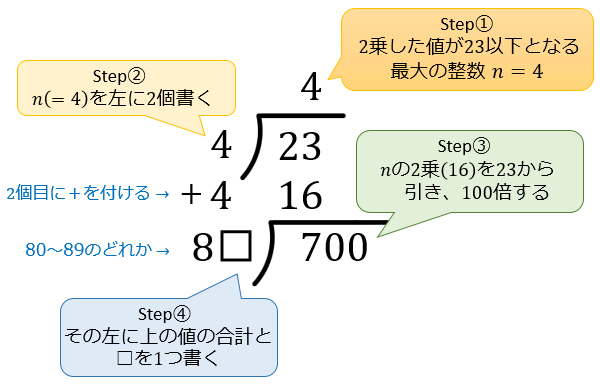
Step⑤ 前のstepで求めた \(8□\) に \(□\) をかけて \(700\) 以下となる最大の \(□\) を探す
※ \(87×7=609\)、\(88×8=704\) より \(□=7\)
Step⑥ \(□\) の値を上に1個、左に2個書く(2個目に+をつける)
Step⑦ \(700\) から \(87×7=609\) を引き、\(100\) 倍する
Step⑧ その左に、上の値 \((87+7)\) の合計と空欄を1つ書く(\(940\) 以上 \(949\) 以下)
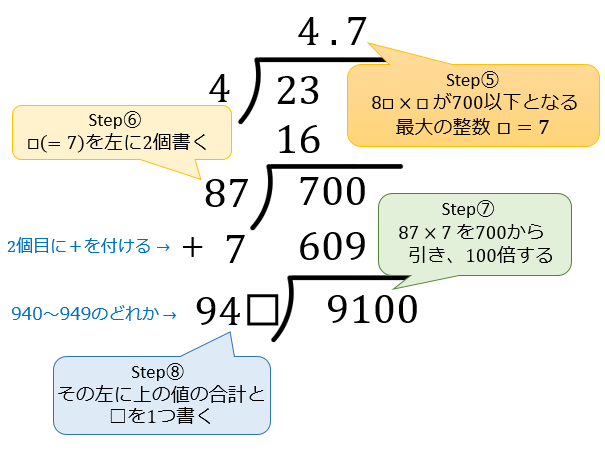
Step⑨「Step⑤からStep⑧」を繰り返す
以上の手順を踏むと、\(\sqrt{23}=4.7958\cdots\) や \(\sqrt{53}=7.2801\cdots\) などの近似値を筆算することができます。
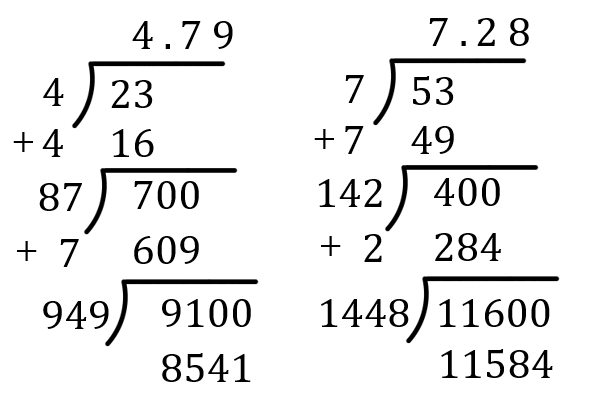
「計算ツールはどうやって平方根を求めているのか?」の考え方の参考として、ぜひ一度筆算を試してみてください。
>>関連記事:平方根√とは何か。計算方法・覚え方・どう役に立つのかを解説