
円周率とは、円の直径に対する円周の長さの比のこと。
英語では “the perimeter of a circle” あるいは単に “Pi” と呼ばれます。
子供のころ「円周率は小数点以下の数字が無限に続いていく数だ」と教わって、その不思議さに心を惹かれたという方も多いのではないでしょうか。
今回は、円周の求め方の公式・円周率とは何なのか・なぜ無限に続くのかについて書いていきます。
photo credit: fdecomite
(1)円周の長さを求める公式は、2×半径×円周率
円周率は、直径を何倍したら円周になるかを表す数字です。
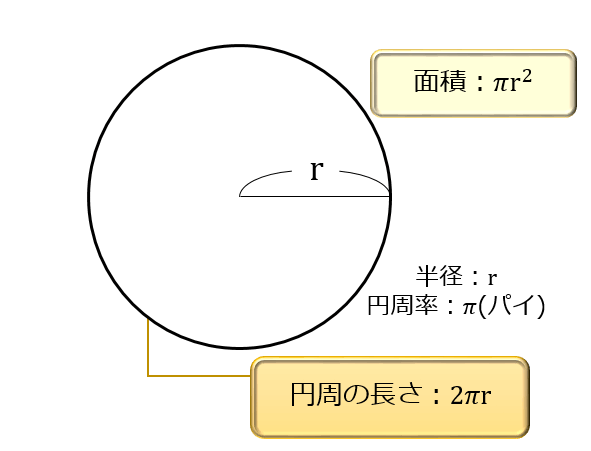
円の半径を r としたら、その2倍が直径 2r 。
ですから、円の直径(2r)に円周率(π≒3.14)をかけることで円周の長さ(2πr ≒ 6.28r)が求まります。
例題①:半径5cmの円の、円周の長さを求めて下さい。
答え:2πr=2π×5=10π
円周率 π を3.14とすると、2πr=2×5×3.14=31.4(cm)
例題②:直径7cmの円の、円周の長さを求めて下さい。
答え:直径 × 円周率=7×π=7π
円周率 π を3.14とすると、7π=7×3.14=21.98(cm)

(2)円周率はどうやって求められるのか?
(1)からも分かる通り、円周の長さを求めるにはまず、円周率を求める必要があります。
皆さんは円周率を単に3.14と習ったと思いますが、これは実用性を考えて簡略化されたもの。
円周率は正確には3.141592…と小数点以下の数字が無限に続いていく特殊な数であることが分かっています。
皆さんはこの話を聞いた時、「小数点以下の小さな数をどうやって正確に求めているんだろう?」と不思議に感じませんか?
その答えは、「正多角形によるはさみうち」にあります。
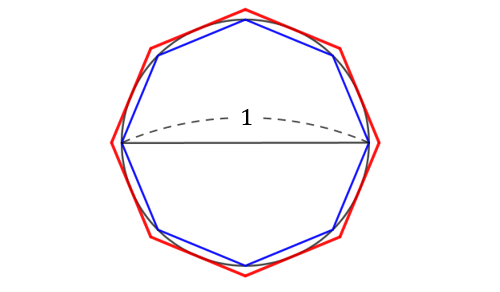
上図は、
① 直径1cmの円
② 直径1cmの円がすっぽり入るような正八角形(外接正八角形)
③ 直径1cmの円にすっぽり入るような正八角形(内接正八角形)
の3つの図形を重ねあわせたものです。
図を見ると「②外接正八角形の外周 > ①円周の長さ > ③内接正八角形の外周」となっていますよね?
そして、円の外周の長さは円周率×1cm
②の外接正八角形の外周の長さを計算すると約3.313708cm
③の内接正八角形の外周の長さを計算すると約3.061467cm
よって、
3.313708 > 円周率×1 > 3.061467
であることがこの時点で分かります。
参考:円に内接する正多角形 円に外接する正多角形|ke!san
(※円の半径を0.5cm=直径1cmで計算)
次に、正八角形の角の数を一気に増やして、正二百角形にしたらどうなるでしょうか。
直径1cmの円の外周の長さは変わらず、円周率×1cm
直径1cmの円に外接する正二百角形の外周の長さは約3.141851cm
直径1cmの円に内接する正二百角形の外周の長さは約3.141463cm
「外接正多角形の外周 > 円周の長さ > 内接正多角形の外周」は二百角形でも同じなので
3.141851 > 円周率×1 > 3.141463
と求まり、この時点で円周率は3.141○○○…と続く数であることが分かります。
このように、角の数を非常に大きな値にすればするほど、円周率の正確な値を絞り込んでいくことができるんです。
(※正多角形の外周の長さは三角関数を用いることで求められます)
(3)円周率は「ループせずに無限に続く数」
さきほど、円周率は3.141592…と小数点以下の数字が無限に続いていく特殊な数だと言いました。
ただ、単に小数点以下の数が無限に続くだけなら1/3=0.3333…もそうであり、驚くほどの物ではありません。
しかし、 円周率はループすることなく無限に続いていくという性質を持っている点で特殊なんです。

数の世界には、このような「ループすることなく無限に続く数」がたくさん存在します。
不思議ですよね。
(4)なぜ、ループせずに無限に続くのか。その正体とは?
(3)の話を聞いて、「ループせず無限に続く数なんて謎すぎる!」と思った方も多いのではないでしょうか。
その謎を解く鍵は、それとは反対に「無限には続かない数」にはどんな性質があるかを考えることで分かります。
というのも、 実は「無限には続かない数」には「必ず分数で表す事ができる」という性質があるんです。

言われてみれば当たり前のことかもしれませんが、これは非常に重要なことです。
なぜなら「無限には続かない数」が「必ず分数で表せる」ということは、ひっくり返して(対偶で)考えれば、「分数で表せない数」こそが円周率を始めとした「ループすることなく無限に続く数」の正体だということになるからです。

円周率を整数による分数で表せないことの証明には難関大学入試レベルの知識が必要ですが、√2を整数による分数で表せないことの証明は簡単にできます。

この証明から、√2は整数による分数では表せないことが分かり、 整数による分数では表せないことから、√2は無限に続く数であることが証明されました。

全く同じ手法で、√3も整数による分数では表せない・無限に続く数であることが証明できます。
ここで「なぜ整数による分数で表せない数があるの?」と疑問に思われるかもしれませんが、それには「実際、√2や円周率は整数による分数で表せないから」としか答えられないです。たとえば「2/5を整数で表して下さい」と言われても、「そんなの無理だよ」となりますよね。そこで「なぜ整数では表せない数があるの?」と質問されても、「実際、2/5は整数で表せないから」と答えるはず。それと同じ感じですね。
(5)円に内接・外接する正多角形の世界では、ループせずに無限に続く数がよく現れる
√2や√3が無限に続く数であると分かったところで、(2)の「円に内接・外接する正多角形の外周」の話に戻りましょう。
この「直径1cmの円に内接・外接する正多角形の外周の長さ」、実は無限に続く数であるケースが多いことが分かっています。
たとえば
直径1cmの円に内接する正方形の外周は2×√2cm→2.828427…(無限に続く)
直径1cmの円に外接する正六角形の外周は2×√3cm→3.464101…(無限に続く)
直径1cmの円に外接する正十二角形の外周は(24 – 12×√3)cm→3.215390…(無限に続く)
このように、直径1cmの円に内接・外接する正多角形の世界では無限に続く数というのは全然珍しくない存在なんです。
(6)円とは「円に内接する無限正多角形」である
ここまで来れば、円周率がなぜ無限に続く数なのかも納得がいくはず。
多角形の角を増やせば増やすほど円に近付いていくことからも分かる通り、円は無限正多角形とも言える存在です。
「直径1cmの円に内接・外接する正多角形の世界では無限に続く数というのは全然珍しくない」
⇒「ゆえに、直径1cmの円に内接する無限正多角形とも言える円の外周・円周率も、無限に続く数であることは何ら特別なことではない」
という訳です。
まとめ
①円周率とは、直径を何倍したら円周になるかを表す数字
②半径をrとしたら、それを2倍にした直径(2r)に円周率(π≒3.14)をかけることで円周が求まる
③円周の内外を正多角形で挟み込み、その正多角形の外周を三角関数を使って調べる事で、円周率の正確な値を絞り込んでいく事ができる
④円周率はループすることなく無限に続く数。このような数は無理数と呼ばれ、√2や√3など数多く存在する
⑤なぜ無限に続くかと言うと、整数による分数では表せない数だから。円周率が分数で表せない数である事の証明は非常に難解だが、√2が分数で表せない数である事の証明は簡単
⑥円に内接・外接する正多角形の世界では、無理数がよく現れる
⑦ゆえに、無限正多角形たる円の外周を表す円周率も、ループすることなく無限に続く数であるなのは特別な事ではない
今回の説明は、分かりやすかったでしょうか?
円周率が無限に続く数である(整数による分数で表せない)ことの証明には、①漸化式②三角関数③微積分(微分・積分)④数学的帰納法という4つの武器を持っている必要があり、高校生はおろか難関大学の理系学部合格者でも自力での証明には苦戦するものです。
ただ、今回の説明で「円周率が無限に続くのは、円周率が整数による分数で表せない数だからなのか。正多角形や円の世界ではこういった数がよく出てくるなんて不思議だな~」くらいには理解していただけたのではないでしょうか。
この記事を通じて、円周率についてもっと深く勉強したい!と思っていただけたら嬉しいです。





