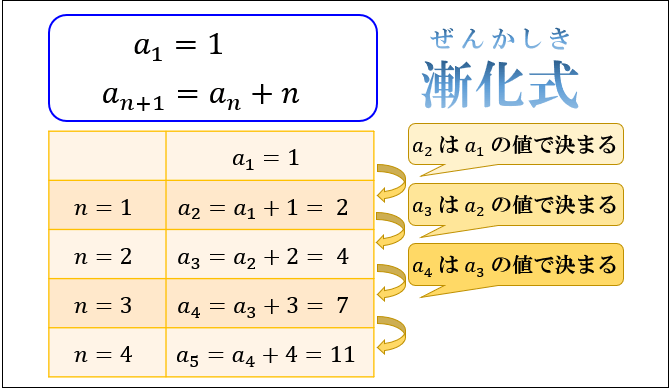
漸化式とは「各項の値がそれより前の項の値によって決まる数列」の規則を表す式のことを言います。
社会・経済・自然科学において「ある時点での値が、それより前の時点での値をベースに決まるもの」は少なくありません。
● ある日の株価は、その前日の株価をベースに決まる
● ある月の集客数は、その前月の集客数をベースに決まる
● ある瞬間の粒子の位置は、その1秒前の位置をベースに決まる
こういった性質をもつ物事において、過去のデータをもとに将来を予測したいとき、「漸化式」というツールは重要な役割を果たしてきます。
今回は、そんな漸化式の基本となる3つのパターンについて見ていきましょう。
基本となる3つのパターン
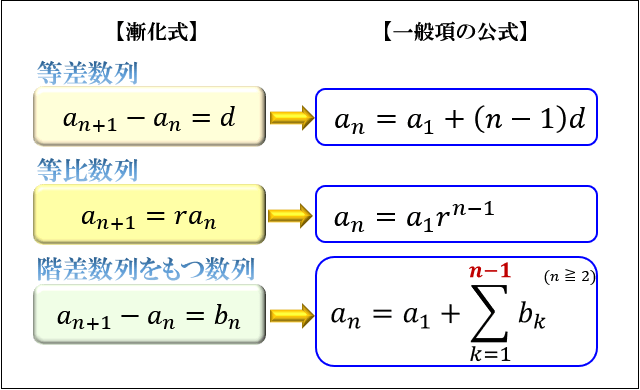
漸化式の基本となるパターンは、以下の3つです。
- 等差数列
- 等比数列
- 階差数列
どのパターンにおいても、漸化式の性質からその数列の一般項を求めるのが目標です。
一般項とは、数列の \(n\) 番目の値 \(a_n\) を \(n\) の式で表したもののこと。
たとえば \(a_n=3n-2\) のように、\(n\) に数字を代入するだけで \(a_n\) を求められるのが特徴。
さきほどの例でいうなら
● ある日とその前日の株価の関係から、\(n\) 日目の株価を予測する
● ある月とその前月の集客数の関係から、\(n\) 月目の集客数を予測する
● ある瞬間とその1秒前の粒子の位置関係から、\(n\) 秒目の粒子の位置を予測する
というのが漸化式を解く目的となります。
① 等差数列パターン
まずは、等差数列から見ていきましょう。
等差数列とは、隣り合う項 \(a_n\) と \(a_{n+1}\) の差が一定である数列のことを言います。
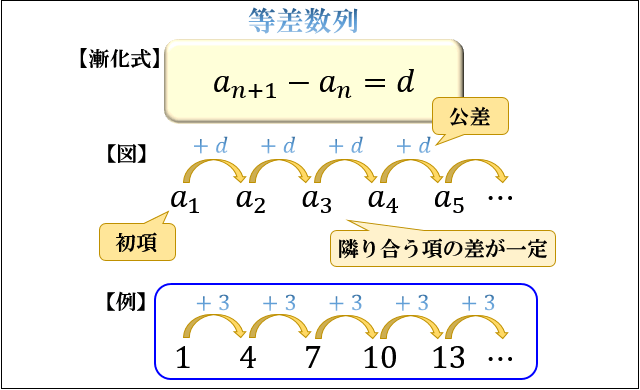
ここで、
数列の \(1\) 番目の値 \(a_1\) のことを「初項 \(a_1\) 」
隣り合う項の差 \(d\) のことを「公差 \(d\) 」
と言います。
「初項 \(a_1\)」「公差 \(d\) 」の等差数列 \( \left\{a_n \right\}\) の一般項を求めるときは
等差数列の一般項の公式\(「a_n=a_1+(n-1)d」\) を使いましょう。

【問①】\(a_1=1\) , \(a_{n+1}=a_{n}+3\) で定められる数列 \( \left\{a_n \right\}\) の一般項を求めてください。
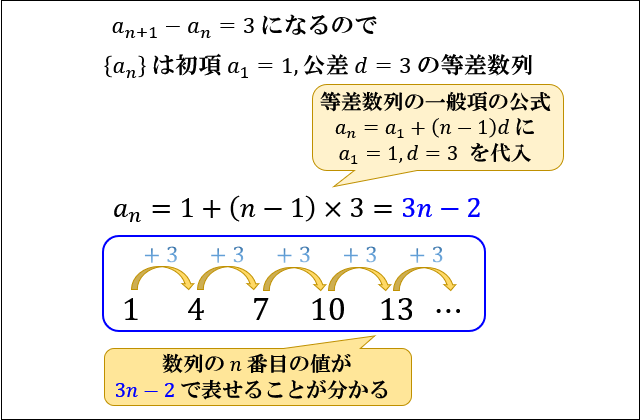
等差数列の一般項の公式\(「a_n=a_1+(n-1)d」\) に代入することで
一般項 \(a_n=3n-2\) が求まりました。
実際に数列をみると
\(n=4\) 番目の値が \(3×4-2=10\)
\(n=5\) 番目の値が \(3×5-2=13\)
と一般項で数列を表せていることが分かりますね。
② 等比数列パターン
さて、等差数列が分かったら、次は等比数列です。
等比数列とは、隣り合う項 \(a_n\) と \(a_{n+1}\) の比が一定である数列のことを言います。
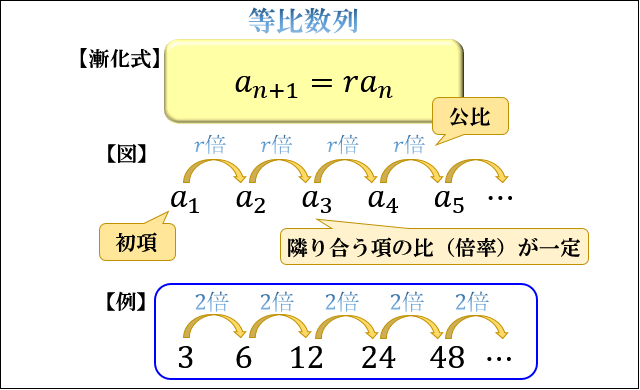
ここで、
隣り合う項の比 \(r\) のことを「公比 \(r\) 」
と言います。
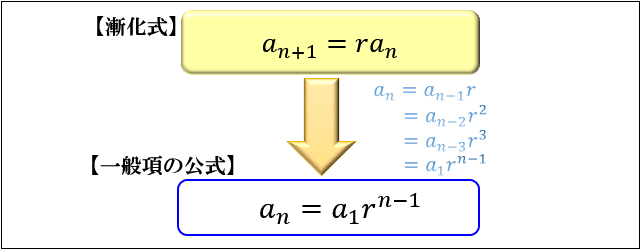
「初項 \(a_1\)」「公比 \(r\) 」の等比数列 \( \left\{a_n \right\}\) の一般項を求めるときは
等比数列の一般項の公式 \(「a_n=a_1×r^{n-1}」\) を使いましょう。
【問②】\(a_1=3\) , \(a_{n+1}+2a_{n}=0\) で定められる数列 \( \left\{a_n \right\}\) の一般項を求めてください。

等比数列の一般項の公式\(「a_n=a_1×r^{n-1}」\)に代入することで
一般項 \(a_n=3×(-2)^{n-1}\) が求まりました。
実際に数列をみると
\(n=4\) 番目の値が \(3×(-2)^{3}=-24\)
\(n=5\) 番目の値が \(3×(-2)^{4}=48\)
と一般項で数列を表せていることが分かります。
③ 階差数列があるパターン
最後は、階差数列をもつ数列です。
隣り合う項 \(a_n\) と \(a_{n+1}\) の差が「 \(n\) の式 \(f(n)\)」で表されるとき
数列 \(b_n=f(n)\) のことを「 \(a_n\) の階差数列」と言います。
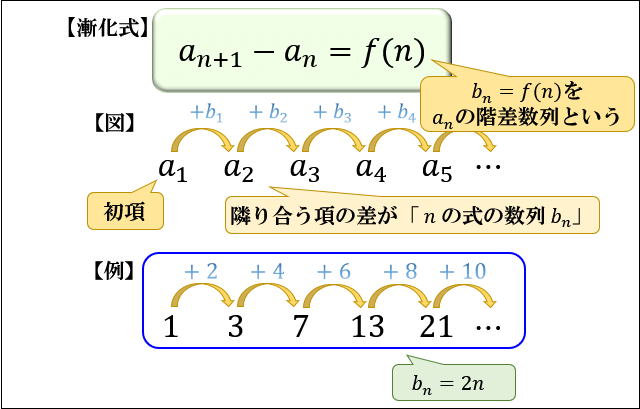
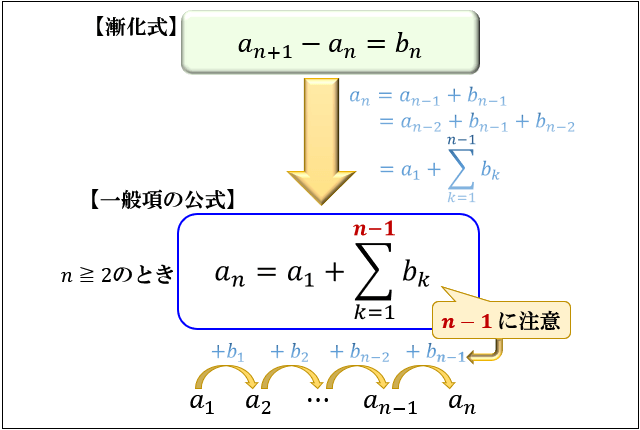
「初項 \(a_1\)」「階差数列 \(b_n\) 」の数列 \( \left\{a_n \right\}\) の一般項を求めるときは
階差数列をもつ数列の一般項の公式を使いましょう。
【問③】\(a_1=1\) , \(a_{n+1}-a_{n}-2n=0\) で定められる数列 \( \left\{a_n \right\}\) の一般項を求めてください。
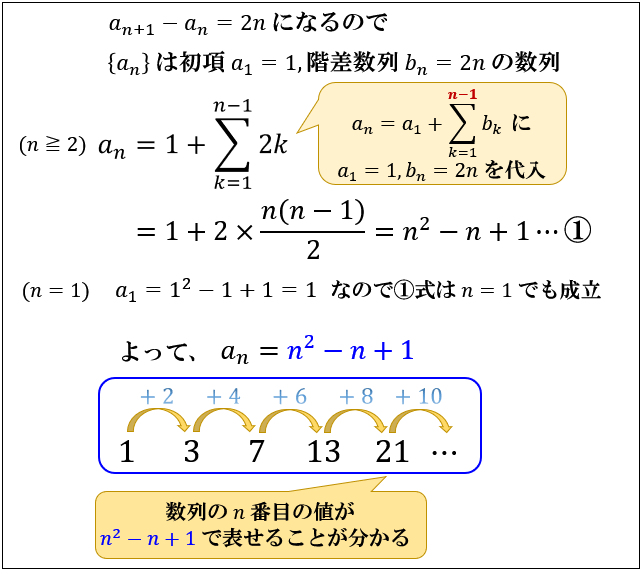
公式に代入することで
一般項 \(a_n=n^2-n+1\) が求まりました。
これも、実際に数列をみれば
\(n=4\) 番目の値が \(4^2-4+1=13\)
\(n=5\) 番目の値が \(5^2-5+1=21\)
と一般項で数列を表せていることが分かります。
さらに難しい漸化式
\(a_{n+1}=pa_n+q\) のようにさらに難しい形の漸化式の場合、「特性方程式」を使って解く必要がでてきます。
それについては次の記事で見ていきましょう。

まとめ
漸化式の「過去の値が将来の値に影響するものについて、時点 \(n\) における値 \(a_n\) を一般化する」という考え方は、さまざまな分野で応用がきく重要な思考法です。
フィボナッチ数列のように、考える事象が複雑になればなるほど解くべき漸化式も難しくなってきますが、根本となる考え方は今回紹介した3つのパターンと変わりません。
今回学んだ \(a_n\) をベースに、次の \(a_{n+1}\) を積み上げていきましょう。




