二次方程式とは、2x2+3x+1=3 のような「xの2乗までを含む方程式」のことを言います。
二次方程式の意味をキチンと理解するために、「方程式」と「2乗する」の意味から確認していきましょう。
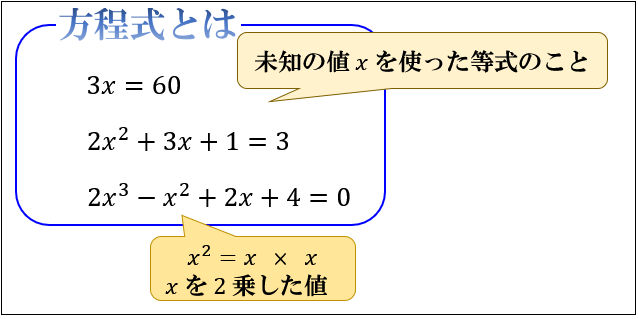
まず、未知の値 \(x\) を使った等式のことを、方程式と言います。
未知の値を \(x\) とおいて、成り立つ等式から \(x\) の値を逆算していくのが方程式の目的です。
そして
\(3^2=3×3=9\) のように同じ数を \(2\) 回かけ合わせることを「 \(2\) 乗する」
\(5^3=5×5×5=125\) のように同じ数を \(3\) 回かけ合わせることを「 \(3\) 乗する」
と言います。
ここで、
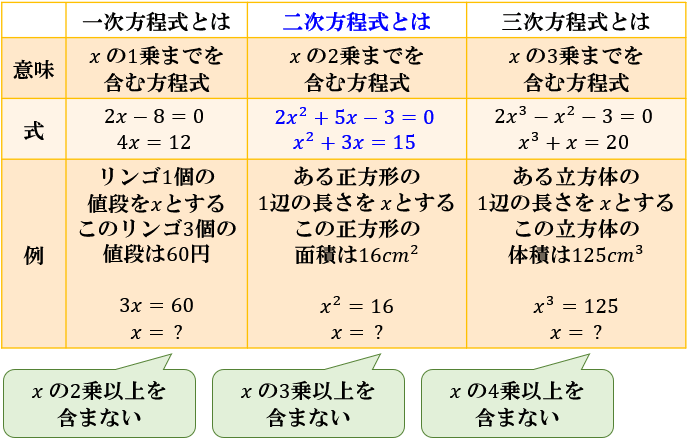
\(3x^2-x=4\) や \(x^2=16\) のように「 \(x\) の \(2\) 乗までを含む方程式」のことを二次方程式
\(2x^3-1=3x^2\) や \(x^3=125\) のように「\(x\) の \(3\) 乗までを含む方程式」のことを三次方程式
と言います。
このページでは、この二次方程式の解き方を見ていきましょう。
二次方程式の3つの解き方
2次方程式の解き方は、大きく分けて3種類あります。
上から順番に見ていきましょう。
(1)平方根
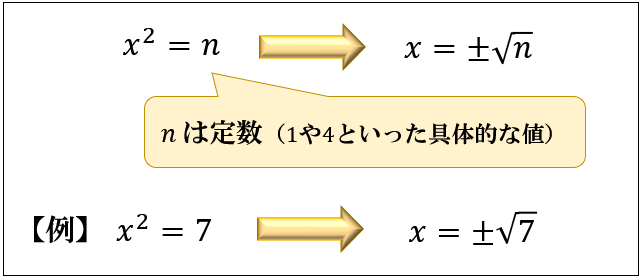
二次方程式は、平方根の性質「\(x^2=n\) のとき、\(x=±\sqrt{n}\)」を利用して解くことができます。
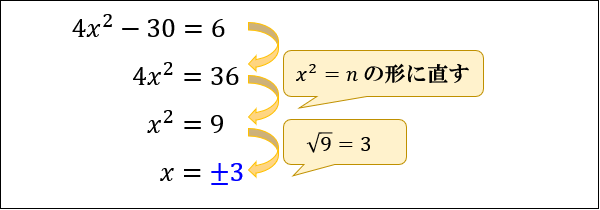
【問①】\(4x^2-30=6\) を解いてください
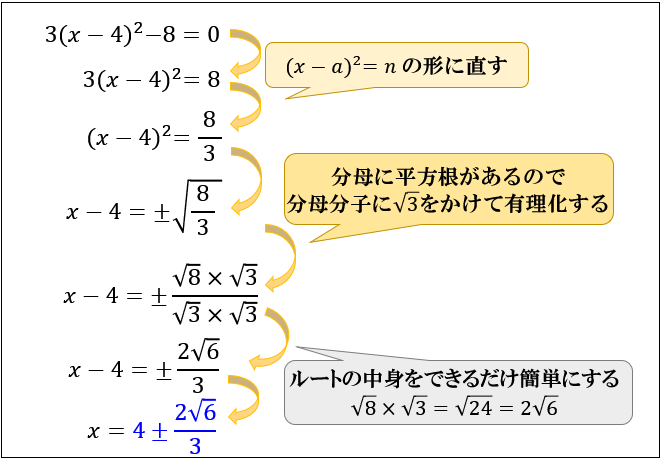
【問②】\(3(x-4)^2-8=0\) を解いてください
「平方根の計算方法まとめ。おさえておくべき4つのポイント」の記事でも解説したように
【平方根のルール】
● ルートの中身をできるだけ簡単にする
● 分母に平方根があるときは、分母の有理化を行う
に気をつけながら計算するのがポイントです。
(2)因数分解による解法
二次方程式\(「ax^2+bx+c=0」\)は、左辺を一次式 \(px+q\) の積に因数分解できれば
\(A×B=0\) ⇔ \(A=0\ または\ B=0\)
を利用することで、その解を求めることができます。
【問③】\(2x^2-2x-12=0\) を解いてください

【問④】\(-12x^2+7x+10=0\) を解いてください

「たすきがけ」については「因数分解の問題の解き方とコツ。2乗・3乗公式とたすきがけ」の記事も参考にしてみてください。
(3)解の公式
解の公式(Ⅰ)型
\(「ax^2+bx+c=0」\)の解は、二次方程式の解の公式に \(a,b,c\) を代入して求めることもできます。

この公式の求め方は「二次方程式の解の公式。導き方・証明法を分かりやすく解説」の記事で紹介しています。
【問⑤】\(x^2+6x+3=0\) を解いてください

【問⑥】問④の方程式、 \(-12x^2+7x+10=0\) を解の公式を用いて解いてください

解の公式(Ⅱ)型
\(「ax^2+bx+c=0」\) の解の公式は、\(b\) が偶数で \(b=2b’\) とおける場合は、少し簡単に求めることができます。

計算時間を短縮できる(約分する手間が減る)というだけで、やっていることは解の公式(Ⅰ)型とまったく同じです。
【問⑦】\(3x^2+8x-4=0\) を解いてください

こちらの公式を使わずとも解の公式(Ⅰ)型からでも求められるので、2つの公式を混同しそうなら、まずは解の公式(Ⅰ)型だけ覚えることを優先しましょう。