● できるだけ少ない資材で、可能な限り大きな容積の建物を作りたい場合
● 斜めに打ちあげたボールの最高点の位置と落下地点を予測したい場合
など、さまざまな場面で登場する二次方程式の計算問題
二次方程式を解くときは、『因数分解』をするか『二次方程式の解の公式』を使います。
どちらを使うか判断するコツとしては、\(x\) に \(-3\) から \(+3\) までを代入したときに等号が成立したら『因数分解』、成立しなさそうなら『2次方程式の解の公式』を使うのがオススメです。
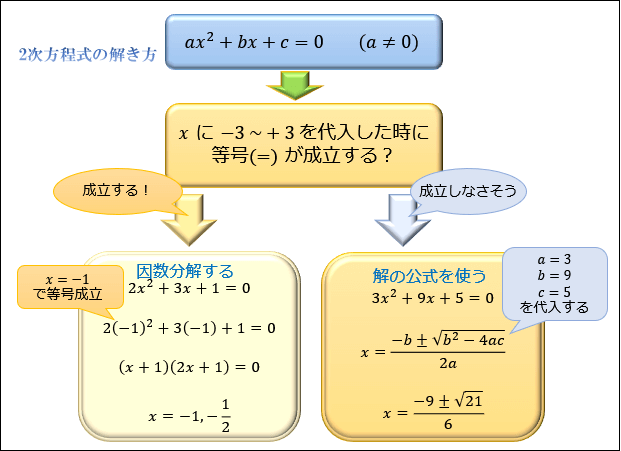
今回は、この解の公式の導出・証明方法を解説していきます。
解の公式の導出(証明方法)
\(「ax^2+bx+c=0 (a≠0)」\) の解の公式の導き方は、大きく分けて7つのステップで構成されています。

Step①両辺をaで割る
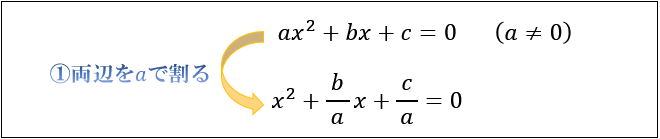
まず、計算をシンプルにするために、両辺を \(a\) で割ります。
数学には 0で割ってはいけないルールがあるので、\((a≠0)\) をキチンと明記したうえで両辺を \(a\) で割るようにしましょう。
\(0÷a=0\) なので、右辺は \(0\) のままです。
Step②平方完成のための値を足して引く
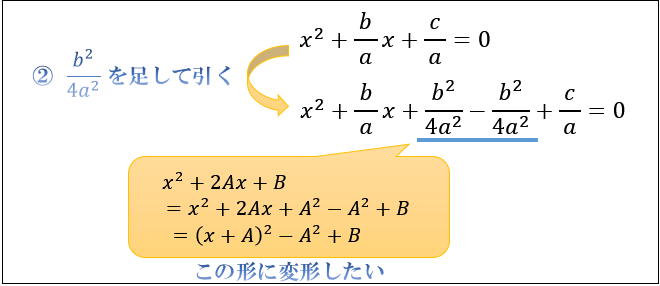
次に、両辺に \(\dfrac{b^2}{4a^2}\) を足して \(\dfrac{b^2}{4a^2}\) を引きます。
\(\dfrac{b^2}{4a^2}-\dfrac{b^2}{4a^2}=0\) なので、右辺は \(0\) のままです。
「同じ数を足して引く」のは、意味のない計算のように見えるかもしれませんが、この『おまじない』が次のステップで活きてきます。
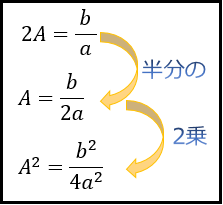
この『おまじない』は、「 \(x\) の項(今回は \(b/a\) )の半分の2乗」と覚えておくと便利です。
Step③平方完成する
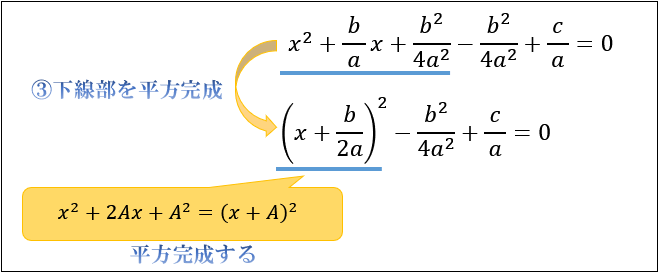
つぎに、上図の下線部に注目してください。
この下線部は、\(A=\dfrac{b}{2a}\) と置くと \(x^2+2Ax+A^2=(x+A)^2\) の形で表せることに気がつくはず。
これを利用して、下線部を \(\left(x+\dfrac{b}{2a}\right)^2\) という形に変形します。
このように、式を \((x+A)^2\) の形に変形することを平方完成と言います。
Step④,⑤残りを右辺に移項して、通分する
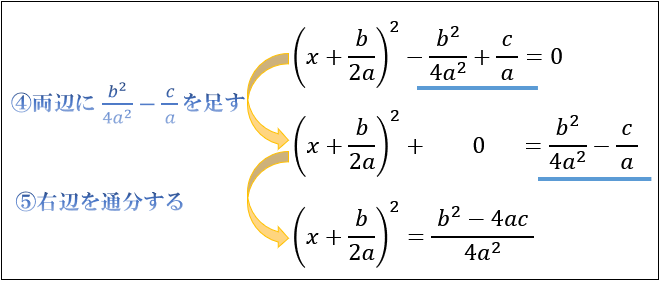
平方完成できたら、\((x+A)^2\) 以外の項を右辺に移項して、通分します。
下線部に注目しながら、「プラスとマイナスを反転させる」ことを忘れずに移項しましょう。
Step⑥,⑦平方根をとって、b/2a を右辺に移項

\((x+A)^2\) 以外の項を右辺に移項したら、式全体が \((x+A)^2=C\) という形になります。
そこで、\(「(x+A)^2=C ⇔ x+A=±\sqrt{C}」\)の公式を使って、両辺の平方根を取ります。
この時、右辺に「 \(±\) (プラスマイナス)」を付けるのを忘れずに
最後に両辺から \(\dfrac{b}{2a}\) を引けば、みごと『解の公式』の完成です!
【全体のおさらい】