平方完成のやり方と平方完成するメリットについて

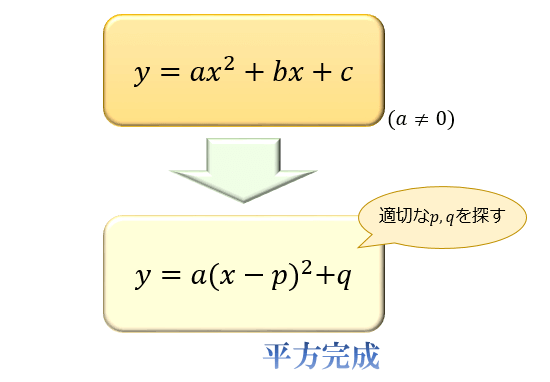
$ax^2+bx+c$ の形の二次式を $a(x-p)^2+q$ の形に変形することを平方完成と言います。

$m^2$ のことを「平方メートル」と呼ぶように、2乗した値のことを「平方」と呼びます。

平方完成とは「平方 $(x-p)^2$ の形を完成させる」という意味です。

この記事では「平方完成のやり方」と「平方完成をするメリット」を見ていきましょう。

平方完成のやり方

問１．$3x^2+18x+16$ を平方完成してください。

平方完成は、以下の4つのステップで行います。

step① $x$ を含む項を「$x^2$ の係数」でくくる

step②カッコ$()$の中で「$x$ の係数の半分の2乗」を足し引きする

step③平方の形を作る

step④中カッコ$\{\}$を外して定数項を整理する

カッコ$()$の中で「$x$ の係数の半分の2乗」を足して引くのが特に重要なポイント。

今回はカッコの中の $x$ の係数は $6$ なので、その半分の2乗である $3^2=9$ を足して引きます。

Tooda Yuuto

これにより $x^2+2dx+d^2=(x+d)^2$ の公式を使って平方の形を作るのが目的です。

一般形 $ax^2+bx+c$ を平方完成して得られるのが、以下の公式。

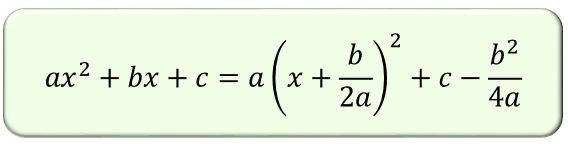
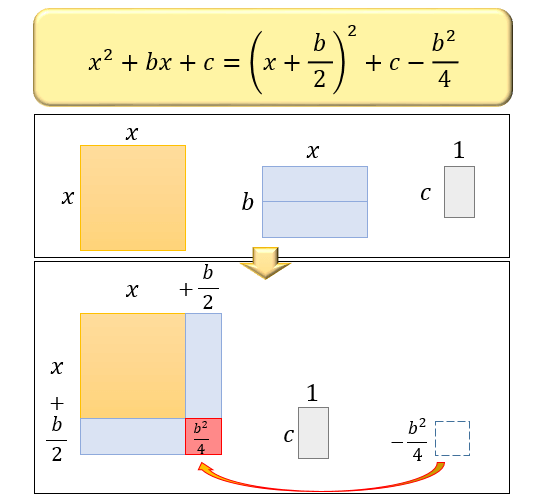
特に $a=1$ のときは $\displaystyle \left(x+\frac{b}{2}\right)^2+c-\frac{b^2}{4}$ となります。

図にするとこんな感じですね。

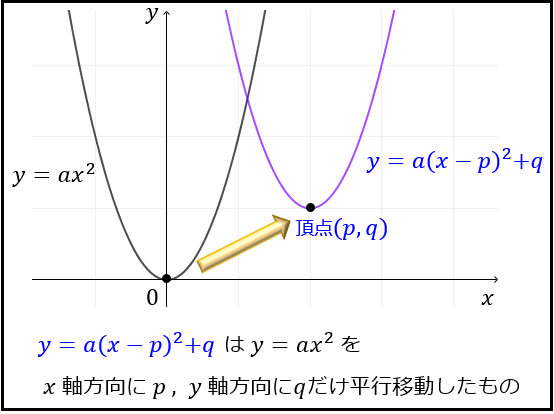
平方完成は二次関数 $y=ax^2+bx+c$ の頂点を求められるので、二次関数のグラフを描きたいときに便利な手法です。

問２．$y=3x^2+18x+16$ のグラフを図示してください。

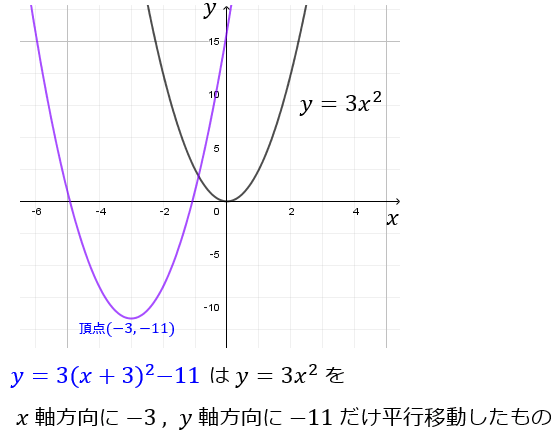
解答． $y=3x^2+18x+16$ を平方完成すると、$y=3(x+3)^2-11$。

よって、$y=3x^2$ を $x$ 軸方向に $-3$ , $y$ 軸方向に $-11$ だけ平行移動した、頂点 $(-3,-11)$ の二次曲線を描けばよい。

また、「実数を2乗したら、必ず $0$ 以上の値になる」という性質があるのも重要なポイント。

例えば、いろんな制約条件のもとで「どの組み合わせならコストを最小化できるか」を考えるときに平方の形を利用したりしますね。

問３．実数 $x,y$ が $2x^2+3xy+2y^2=3$ を満たす時、$x+y+xy$ の最小値はいくつか？