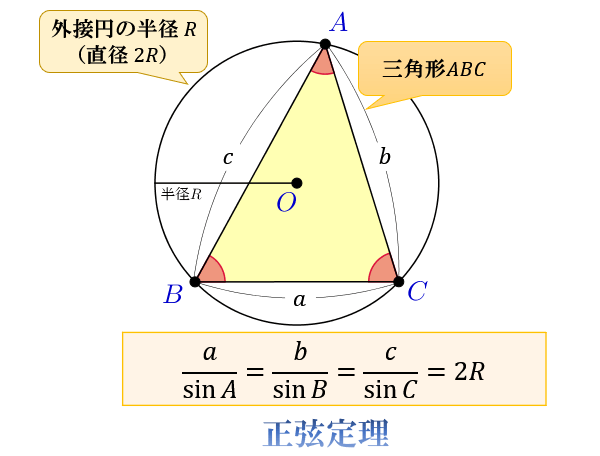
三角形 \(ABC\) について、点 \(A,B,C\) の内角をそれぞれ角 \(A,B,C\) とおき
点 \(A\) の反対側にある線分 \(BC\) の長さを \(a\)
点 \(B\) の反対側にある線分 \(CA\) の長さを \(b\)
点 \(C\) の反対側にある線分 \(AB\) の長さを \(c\)
とおいたときに、以下の3つの式が成り立つことを余弦定理と言います。

余弦定理は、「2辺の長さとその間の角度」から「残り1辺の長さ」を求めたり、「3辺の長さ」から「3つの角度」を求めるのに使います。
2辺+角度⇒残り1辺の長さ
まずは、「2辺の長さとその間の角度」から「残り1辺の長さ」を求める場合。
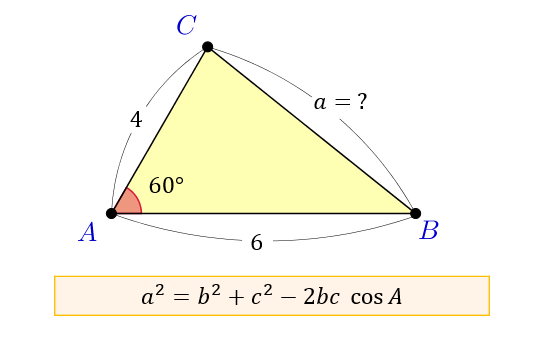
\(b=AC=4\)
\(c=AB=6\)
\(\cos{A}=\cos{60°}=\dfrac{1}{2}\)
を代入すると、残り1辺の長さ \(a\) が求まります。
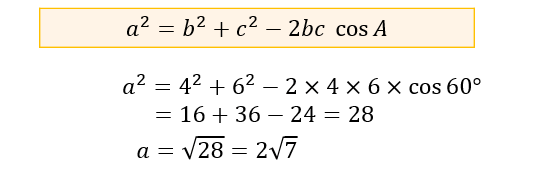
3辺の長さ⇒角度
次に、3辺の長さから角度を求める場合。
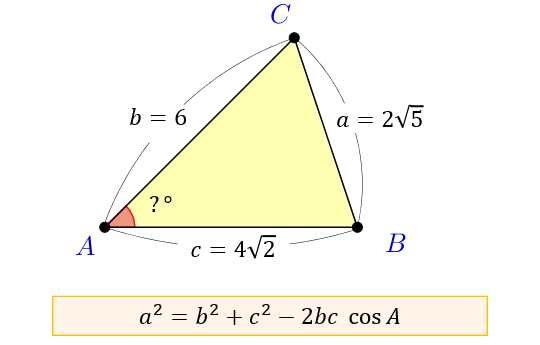
この場合は、余弦定理の式を「\(\cos{A}=\cdots\)」の形に式変形してから \(a,b,c\) を代入すると
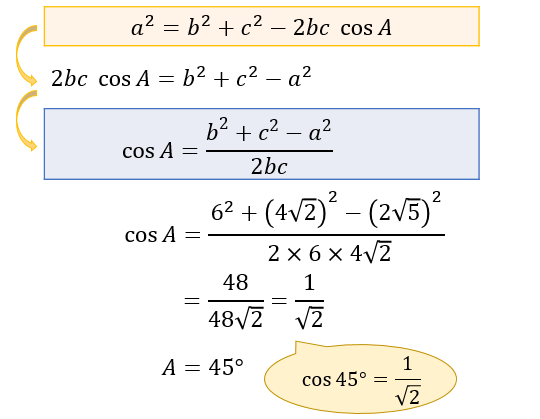
\(\cos{A}=\dfrac{1}{\sqrt{2}}\) と求まり、\(A\) の内角が \(45°\) であることが分かります。
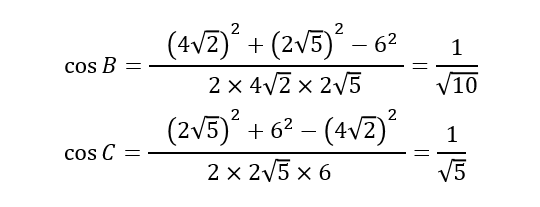
同じように計算すると、\(\cos{B}\) と \(\cos{C}\) も求まります。
余弦定理の証明(鋭角)
余弦定理は、点 \(C\) から直線 \(AB\) に垂線を下すことで証明できます。
まずは角 \(A\) が \(90°\) より小さい場合。
直線 \(AB\) と垂直に交わる線分 \(CD\) を考えたとき、直角三角形 \(ACD\) に注目すると、三角関数の定義から \(CD=b\ \sin{A}, AD=b\ \cos{A}\) であることが分かります。
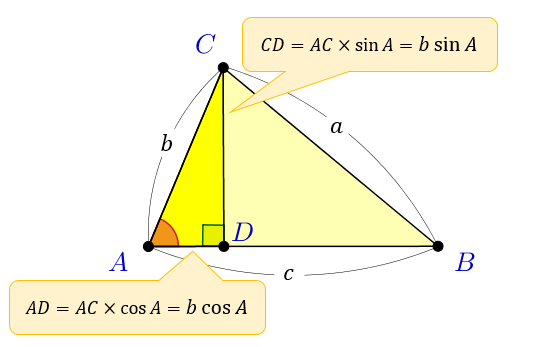
\(CD\) と \(AD\) の長さが分かったら、今度は右側の直角三角形 \(BCD\) に注目。
\(BCD\) は直角三角形なので、その3辺について三平方の定理 \(BC^2=CD^2+DB^2\) が成り立ちます。
ここに \(BC,CD,DB\) の値を代入すると・・・
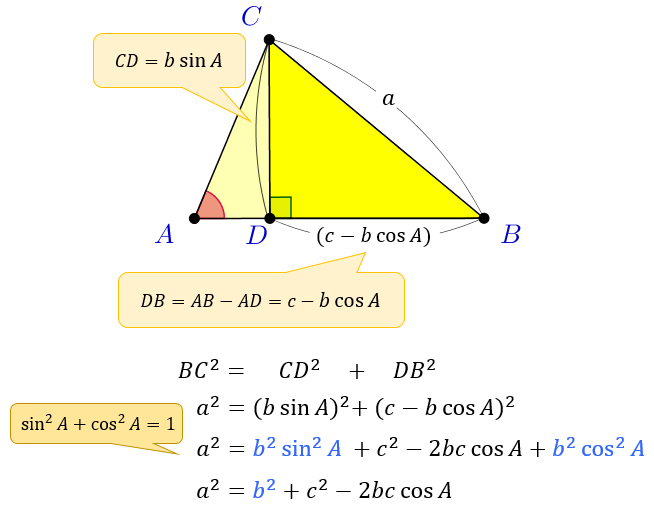
余弦定理が成り立ちます。
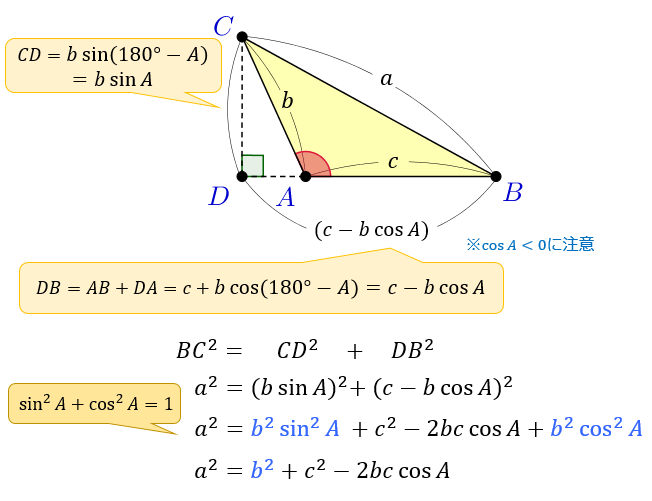
余弦定理の証明(鈍角)
次は、角 \(A\) が \(90°\) より大きい場合。
こちらも \(\cos{A}<0\) であることに注意しつつ、ほとんど同じ流れで証明できます。