直角三角形において、「直角」をはさむ2つの辺の長さを \(a,b\)、斜辺の長さを \(c\) としたとき
\(a^2+b^2=c^2\)
が成り立つことを、三平方の定理と言います。
三平方の定理は、別名「ピタゴラスの定理」とも言います。
例えば、直角をはさむ2つの辺の長さが \(3cm\) と \(4cm\) の直角三角形の斜辺の長さを実際に測ってみると、\(5cm\) であることが分かります。
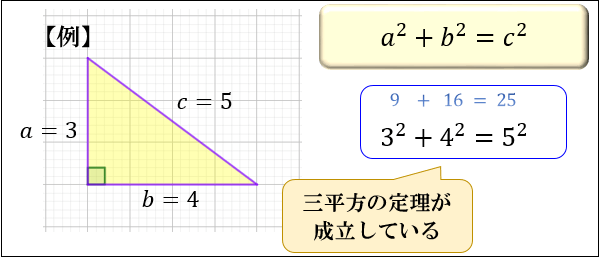
ここで、\(a=3,b=4,c=5\) を代入すると
\(a^2+b^2=3^2+4^2=9+16=25\)
\(c^2=5^2=25\)
となり、三平方の定理 \(a^2+b^2=c^2\) が成立していることが分かりますね。
このページでは、そんな三平方の定理について見ていきましょう。
三平方の定理の証明
まず、下図のように同じ直角三角形を4つ並べて、\(1\) 辺の長さ \((a+b)\) の正方形を作ります。
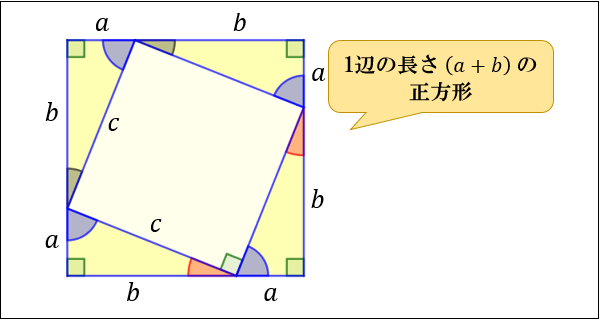
この \(1\) 辺の長さ \((a+b)\) の正方形は
● 真ん中にある \(1\) 辺の長さ \(c\) の正方形と
● 高さ \(a\) 底辺 \(b\) の直角三角形 \(×\ 4\)つ
からできています。
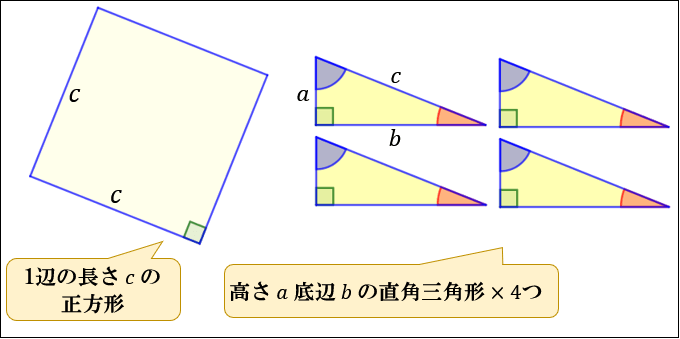
そのため
\(1\) 辺 \((a+b)\) の正方形の面積 \(=1\) 辺 \(c\) の正方形の面積 \(+\) 直角三角形の面積 \(×\ 4\)
が成り立つことが分かります。
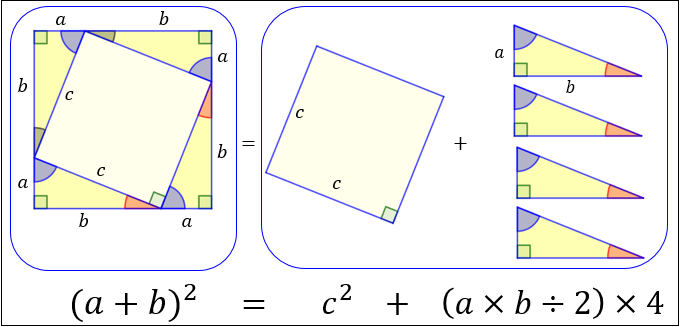
\(1\) 辺の長さ \((a+b)\) の正方形の面積は \((a+b)^2\)
\(1\) 辺の長さ \(c\) の正方形の面積は \(c^2\)
高さ \(a\) 底辺 \(b\) の直角三角形の面積は \(a×b÷2\)
なので
\((a+b)^2=c^2+(a×b÷2)×4\)
⇔ \(a^2+2ab+b^2=c^2+2ab\)
⇔ \(a^2+b^2=c^2\)
となり、三平方の定理を証明できました。
三平方の定理を使った問題
【問①】下図の直角三角形の斜辺の長さ \(c\) を求めてください。
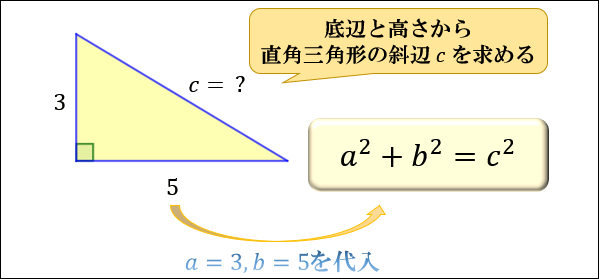
三平方の定理 \(「a^2+b^2=c^2」\) に
\(a=3,b=5\) を代入すると
\(3^2+5^2=c^2\)
⇔ \(9+25=c^2\)
⇔ \(34=c^2\)
よって、\(c=\sqrt{34}\) となります。
\(\sqrt{34}\) は「\(34\) の正の平方根」と言って、二乗したら \(34\) になる正の数のことを指します。
\(\sqrt{34}×\sqrt{34}=34\)
【問②】下図の直角三角形の高さ \(a\) を求めてください。
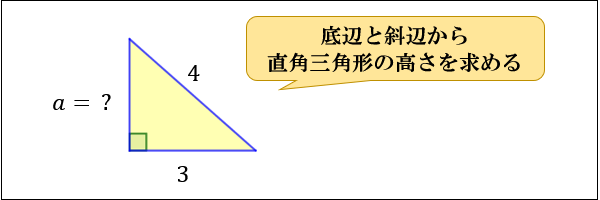
底辺と斜辺から「直角三角形の高さ \(a\) 」を求めます。
三平方の定理に \(b=3,c=4\) を代入すると
\(a^2+3^2=4^2\)
⇔ \(a^2+9=16\)
⇔ \(a^2=7\)
よって、\(a=\sqrt{7}≒2.646\) となります。
忍者が用いた三平方の定理の知恵
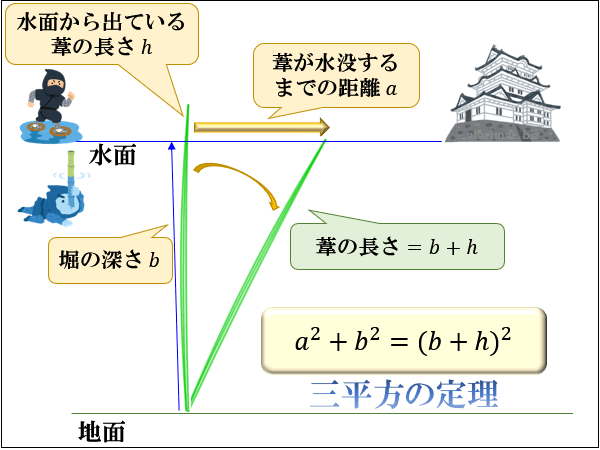
その昔、忍者は敵城の周りの堀の深さを予測するのに三平方の定理を使ったといわれています。
【問③】葦が堀の水面から \(10cm\) 出ています。
葦を横に引っ張ったところ、\(a=50cm\) 横に引いたところで葦が水没しました。
この堀の深さは何\(cm\) と考えられるでしょうか?
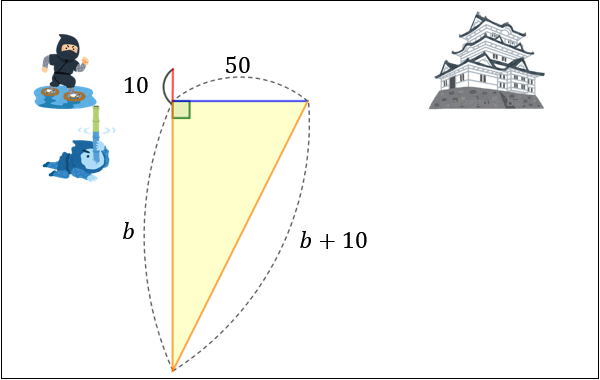
三平方の定理 \(「a^2+b^2=c^2」\) に
\(a=50\)
\(c=b+10\)
を代入すると
\(50^2+b^2=(b+10)^2\)
⇔ \(2500+b^2=b^2+20b+100\)
⇔ \(2400=20b\)
⇔ \(b=120\)
となり、堀の深さは \(120cm\) であることが分かります。
【問④】問③において、\(a=80cm\) 横に引いたところで葦が水没した場合
この堀の深さは何\(cm\) と考えられるでしょうか?
\(a=80\)
\(c=b+10\)
を代入すると
\(80^2+b^2=(b+10)^2\)
⇔ \(6300=20b\)
⇔ \(b=315\)
となり、堀の深さは \(315cm\) であることが分かります。
三平方の定理を用いて水深を予測することで
- 水蜘蛛を使って渡る
- 水遁の術を使う
- 深すぎるので迂回する
といった判断を行っていたのかもしれませんね。