最小公倍数や最大公約数を求めたい場合、その数が何の倍数なのかを調べる必要があります。
しかし、数が大きくなってくるとパッと見では「この数は何の倍数なのか?」が分かりにくくなってくるものです。
そんなとき各数の倍数判定法を知っていると、計算速度があがってテストで時間切れになる可能性を減らすことができるので、非常に便利です。
そこで今回は、2~9の倍数判定法について書いていこうと思います。
2の倍数の判定法
ある数が2の倍数かどうかを判定したいなら、下1ケタ(しもひとけた)に注目しましょう。
もし、下1ケタが2の倍数なら、その数自体も2の倍数です。

3の倍数の判定法
ある数が3の倍数かどうかを判定したいなら、すべての位の数を合計してみてください。
すべての位の数を合計していった答えが3の倍数なら、元の数も3の倍数です。
なぜなら、「すべての位の数を合計しても、3の倍数かどうかは変わらない」からです。

4の倍数の判定法
ある数が4の倍数かどうかを判定したいなら、下2ケタに注目しましょう。
もし、下2ケタが4の倍数なら、その数自体も4の倍数です。

5の倍数の判定法
ある数が5の倍数かどうかを判定したいなら、下1ケタに注目しましょう。
もし、下1ケタが「0または5」なら、その数は5の倍数です。

6の倍数の判定法
ある数が6の倍数かどうかを判定したいなら、「2の倍数判定法」と「3の倍数判定法」を組み合わせてみましょう。
両方の判定法で「この数は2の倍数であり、3の倍数でもある」と分かれば、その数は6の倍数となります。

7の倍数の判定法
ある数が7の倍数かどうかを判定したい場合。
7の倍数の判定法は難しく、素直に7で割った方が早いケースも多いです。
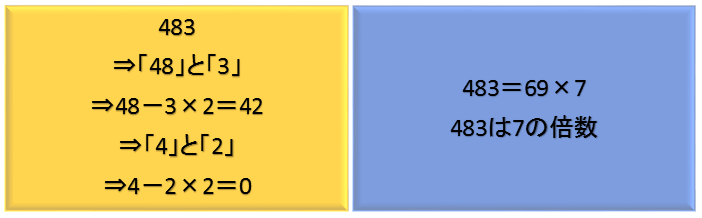
ただ、「483」や「4088」といった3ケタ~4ケタの数であれば、良い方法があります。
それは「下1ケタをぬいた数」から「下1ケタの数の2倍」を引く、を繰り返すことです。
なぜなら【「下1ケタをぬいた数」から「下1ケタの数の2倍」を引く】を行っても「7の倍数かどうかは変わらない」ことが分かっているからです。
最終的に7,21,35といった分かりやすい7の倍数になるか、「0または-7,-14」になればその数は7の倍数です。
5ケタ以上の数なら、素直に7の割り算をしたほうが早いでしょう。
8の倍数の判定法
ある数が8の倍数かどうかを判定したいなら、下3ケタに注目しましょう。
もし、下3ケタが8の倍数なら、その数自体も8の倍数です。

3ケタの数が8の倍数かは実際に割ってみるしかないので、ちょっと手間ですね。
9の倍数の判定法
ある数が9の倍数かどうかを判定したいなら、すべての位の数を合計してみてください。
なぜなら、「すべての位の数を合計しても、9の倍数かどうかは変わらない」からです。

まとめ
2の倍数⇒「下1ケタ」が2の倍数
3の倍数⇒「すべての位の数」を足した合計が3の倍数
4の倍数⇒「下2ケタ」が4の倍数
5の倍数⇒「下1ケタ」が0または5
6の倍数⇒2の倍数であり、3の倍数である
7の倍数⇒【「下1ケタをぬいた数」ひく「下1ケタ×2」】を繰り返しても7の倍数のまま
8の倍数⇒「下3ケタ」が8の倍数
9の倍数⇒「すべての位の数」を足した合計が9の倍数
「あれ、これは何の倍数だろう?」となったときに、ぜひ活用してください!