素因数分解のやり方。5つのステップで分かる素因数分解問題の解き方とコツ

ある整数を「素数のかけ算」の形に変形することを素因数分解(prime factorization)と言います。

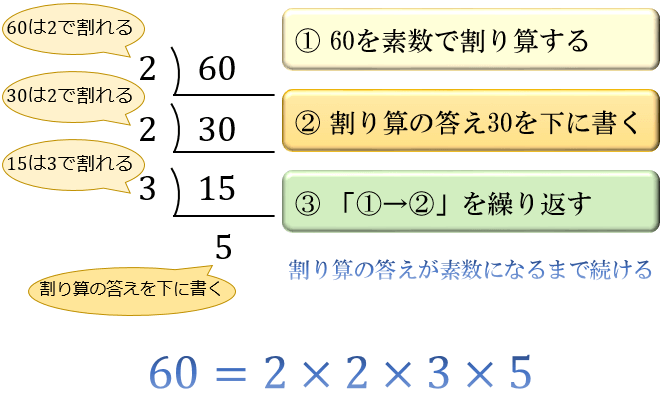
たとえば、\(60\) を素因数分解すると

という素数のかけ算の形に変形することができます。

今回は、この素因数分解のやり方を5つのステップを通じて見ていきましょう。

素数・素因数分解の意味

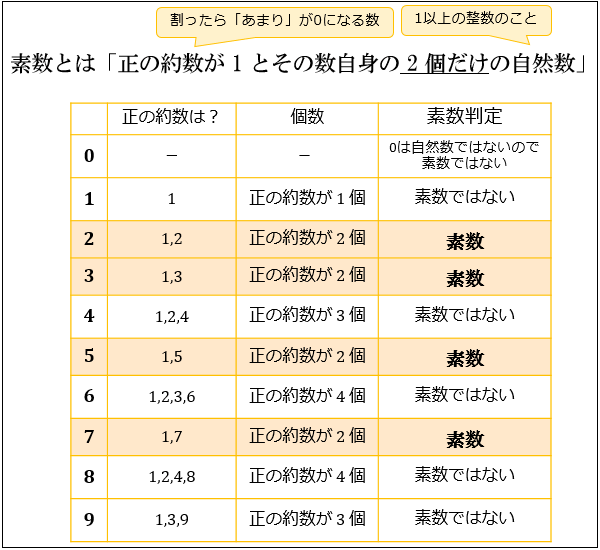
まず、「正の約数が \(1\) とその数自身の2個だけである自然数」を素数と言います。

そして、素因数分解とは「ある自然数を素数のかけ算の形に変形すること」を指します。

たとえば、\(6\) を素因数分解すると \(6=2×3\) となります。

一方、\(12=4×3\)　や　\(18=2×9\) はまだ素因数分解できていません。

なぜなら、\(4\) や \(9\) は素数ではないからです。

さらに分解して、\(12=2×2×3\)　や　\(18=2×3×3\) まで分解して初めて「素因数分解した」と言えることになります。

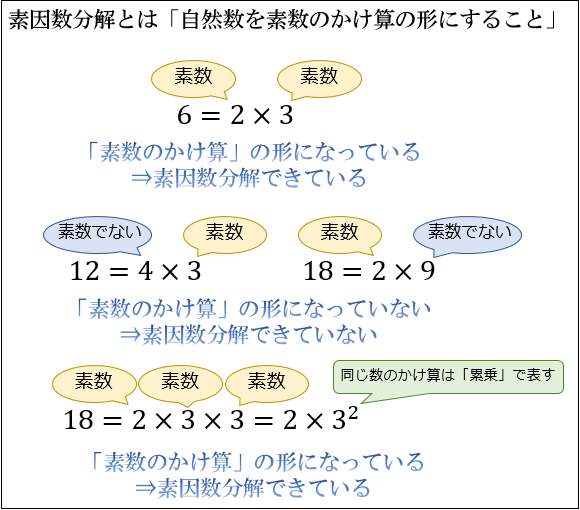
また、 \(81=3×3×3×3\) のように同じ数のかけ算があるときは、短く表すために \(81=3^4\) のように累乗の形で表した方が良いでしょう。

\(64=2×2×2×2×2×2\) なんて、書くのも読むのも大変ですよね。

これも、累乗を使えば「\(2\) を \(6\) 回かけ合わせた数」⇒ \(64=2^6\) とスッキリした形で書くことができます。

素因数分解のやり方

それでは実際に、\(60\) を素因数分解してみましょう。

素因数分解は、以下の5つのステップで行います。

Step① 分解したい数の左下にＬ字のような記号を書く

まず、分解したい数を真ん中に書いてから、その左下に下図のようなＬ字に近い記号を書きます。

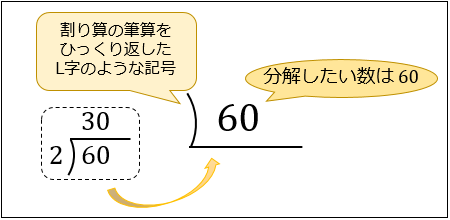
この記号は、割り算の筆算をひっくり返した記号で、割り算の筆算と同じような使い方をします。

Step② 分解したい数を素数で割り算する

次は、「(1)分解したい数」を「(2)素数」で割り算します。

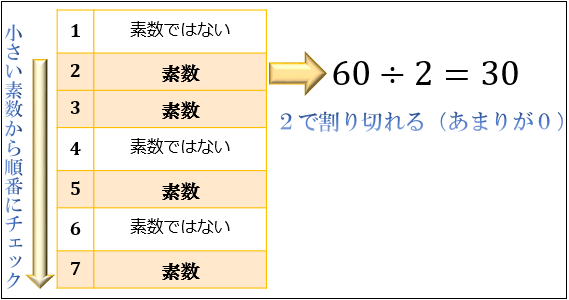
このときのポイントは、小さな素数から順番に割りきれるかどうかチェックしていくこと。

素数は小さい順に \(2,3,5,7,\cdots\) とあるので、まずは \(2\) で割りきれるか確かめてみましょう。

今回は \(60÷2=30\) から、 \(2\) で割り切れることが分かりますね。

Step③ L字の左に「割った数」、下に「割り算の答え」を書く

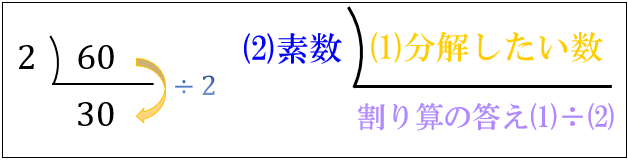
「(1)分解したい数」を割れる「(2)素数」が見つかったら

L字記号の左に「(2)素数」を書いてから、

L字記号の下に「割り算の答え(1) \(÷\) (2)」を書きましょう。

今回は \(60÷2=30\) なので、以下のようになります。

Step④ 「割り算の答え」が素数になるまで分解しつづける

ここからは、Step②とStep③をひたすらくり返します。

「割り算の答え」が素数になるまで、ガンガン分解していきましょう。

次に分解したい数は、\(30\) です。

分解したい数 \(30\) を割り切れる一番小さい素数は \(2\) ですよね。

\(2\) で割り算すると \(30÷2=15\) となるので、以下のようになります。

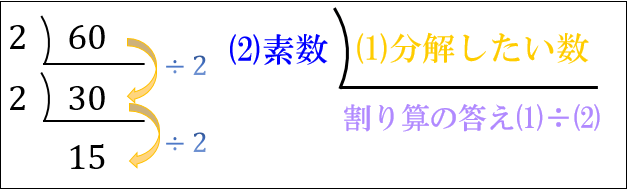
すると、次に分解したい数は \(15\) に。

\(15\) は \(2\) では割り切れないので、今度は \(3\) で割り切れるかチェックします。

\(15÷3=5\) で割り切れるので、以下のようになります。

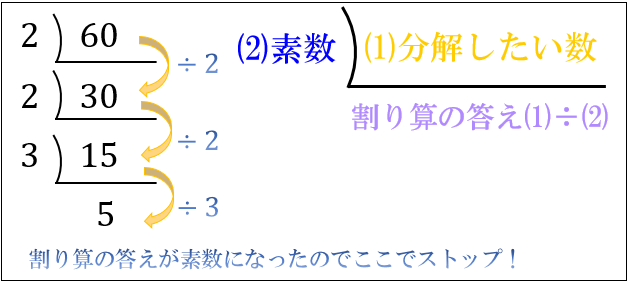
ここで割り算の答えが \(5\) 、つまり素数になりました。

割り算の答えが素数になったら、そこで分解は終わりです。

Step⑤ L字の左側のすべての数と一番下の素数のかけ算を書く

割り算の答えが素数になったら、最後に「L字の左側にあるすべての素数」と「一番下の素数」のかけ算を書いてください。

今回は \(2,2,3,5\) なので、\(2×2×3×5\) になります。

これで、素因数分解が完了です。

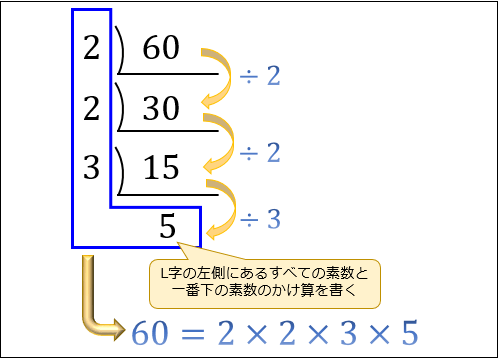
今回は \(2\) が2回かけられているので、それを累乗の形にまとめておきましょう。

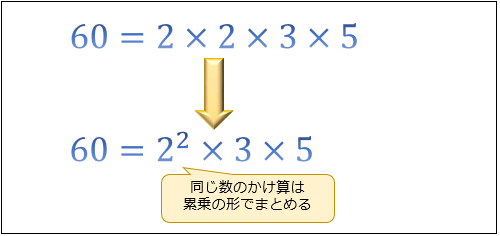
以上から、\(60\) を素因数分解すると

になることが分かりました。

まとめ

素因数分解は、最大公約数や最小公倍数を素早く求めるときのテクニックとして重宝するほか、RSA暗号という形で重大な情報のセキュリティを守るのに貢献している重要な考え方です。

今回紹介した5つのステップを使えばカンタンにマスターできるので、ぜひ繰り返し練習してみてください。