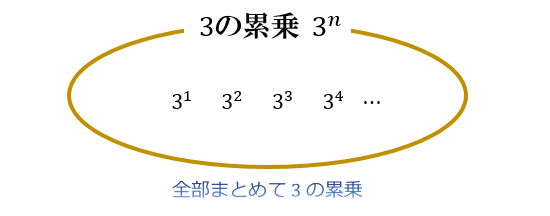
同じ数をくり返しかけ算したもののことを、累乗と言います。
たとえば \(3\) を \(4\) 回かけ合わせた場合、\(3×3×3×3\) となりますよね。
累乗では、これを \(3^4\) と書いて「\(3\) の \(4\) 乗」と読みます。
累乗には、「何回も繰り返しかけ算した値をカンタンに表記できる」というメリットがあります。
たとえば、「\(3\) を \(100\) 回かけ合わせた値」はとてつもなく大きくなってしまうので、まず書き切れませんよね。
こういった場合に累乗を利用すれば、 \(3^{100}\) とスッキリ書くことができます。
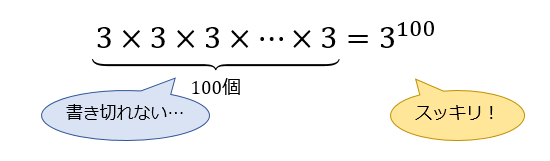
今回は、そんな累乗について解説していきます。
累乗と底・指数
\(a\) を \(n\) 回かけ合わせた値 \(a^n\) のことを、\(a\) の累乗と言います。※ \(n\) は自然数(正の整数)
このとき
\(a\) は底と言って、「繰り返しかけ算する数」
\(n\) は指数と言って、「何回かけ合わせたかを表す数」
を意味しています。
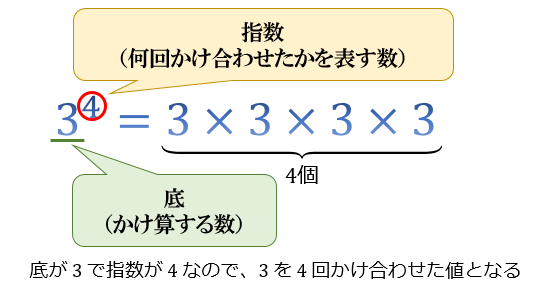
\(3^4\) なら、底が \(3\) ・指数が \(4\) なので「\(3\) を \(4\) 回かけ合わせた値」といった感じですね。
累乗の計算方法
累乗の主な公式は、以下の3つです。
● \(a^m×a^n=a^{(m+n)}\)
● \((a^m)^n=a^{mn}\)
● \((ab)^m=a^m\cdot b^m\)
※ \(a\neq0 , b\neq0\) で \(m,n\) は自然数(正の整数)
上から順番に、例題を通じてみていきましょう。
問1.\(a^2×a^3\) を求めて下さい。
累乗と累乗のかけ算は、指数を足し算することで求まります。
\(a^2×a^3=(a×a)×(a×a×a)\)
\(=a^5\)
「\(a\) を \(2\) 回かけた値」と「\(a\) を \(3\) 回かけた値」をかけたら、 \(a\) を \(2+3=5\) 回かけるのと同じですよね。
問2.\((a^2)^3\) を求めて下さい。
累乗の累乗は、指数をかけ算することで求まります。
\((a^2)^3=(a×a)×(a×a)×(a×a)\)
\(=a^6\)
「\(a\) を \(2\) 回かけた値」を \(3\) 回かけたら、 \(a\) を \(2×3=6\) 回かけるのと同じですね。
問3.\((2×5)^3\) を求めて下さい。
\((2×5)^3=(2×5)×(2×5)×(2×5)\)
\(=(2×2×2)×(5×5×5)=2^3\cdot 5^3\)
指数はどこにかかってる?
負の数が絡んだ累乗の計算をするときは、指数がどこにかかっているかに注目してみてください。
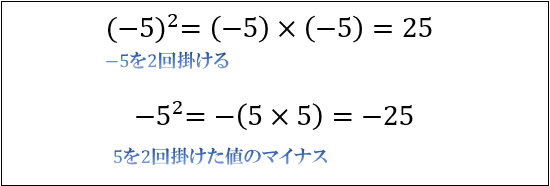
上の例では \(-5\) に指数がかかっていますよね。そのため、\(-5\) を \(2\) 回かけた \(25\) になります。
その一方、下の例では \(5\) に指数がかかっていますね。そのため、\(5\) を \(2\) 回かけた値のマイナスで \(-25\) になります。
パッと見はよく似ているせいで、うっかり間違えてしまいやすいポイントなので注意。
累乗とべき乗
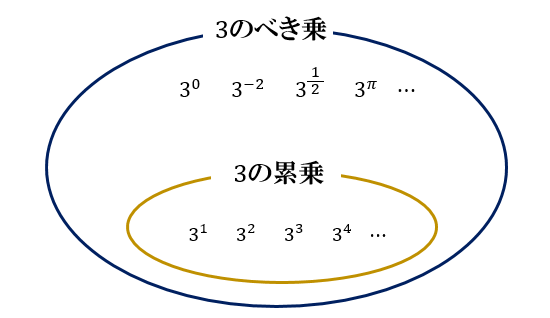
累乗は、\(n\) が自然数(正の整数)の場合のみを考えます。
つまり、 \(n=0\) や \(n=-2\)、\(n=\frac{1}{2}\) などの「自然数以外の数」は考えないということです。
確かに、「\(3\) を \(\frac{1}{2}\) 回かけ算する」では直感的には意味が分からないですよね。

しかし、直感的でないとしても論理的に矛盾しなければ研究を進めていくのが数学。
実は \(a\) の \(n\) 乗「\(a^n\)」において、\(n\) を自然数から実数に拡張した数も存在しています。
この \(n\) を実数全体(さらには複素数全体)で考えたときの \(a^n\) のことを \(a\) のべき乗と言います。
「\(3\) を \(\frac{1}{2}\) 回かけ算なんてできないよ。べき乗なんて考えても役に立たないんじゃないの?」と思う方もいるかもしれませんが、実は \(a\) のべき乗は幅広い領域で役に立っています。
たとえば統計学では、大規模な模試の点数分布や全国の成人男性の身長分布など様々な場所で見かける正規分布・一定の時間内における発生確率を表すポアソン分布などでも「べき乗」が大活躍しています。
累乗・べき乗を理解すると、見えてくる世界が広がってきますよ。