\(2^3\) や \(3^4\) に限らず、\(3^{-2}\)・\(5^\frac{1}{2}\)・\(8^π\) といった値も含めた「\(a\) の \(n\) 乗」の形で表される数 \(a^n\) のことを「\(a\) のべき乗」と言います。
この記事では、べき乗の定義と「\(3^{-2}\)・\(5^\frac{1}{2}\)・\(8^π\) とは具体的にどういう意味なのか?」について書いていこうと思います。
「そもそも、 \(2^3\) や \(3^4\) ってどういう意味?」という方は、ぜひ「累乗とは。その意味と計算方法を解説」の記事から読んでみてください。
べき乗の意味。累乗との違いは?
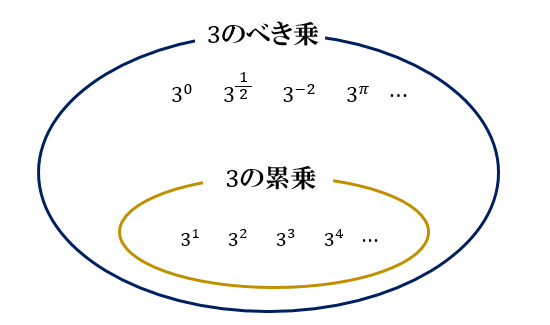
累乗とべき乗は、どちらも \(a^n\) で表されます。
一見すると同じ意味のようにも思えますが、厳密には
● 累乗は \(n\) が自然数(正の整数)に限定されている
● べき乗は \(n\) が実数全体(さらには複素数全体)に拡張されている
という違いがあります。
※「累乗とべき乗は全く同じ『 \(n\) 乗する』という意味であり、\(n\) が自然数なのか実数なのかは問わない。べき乗の方が古い言い方なだけ」とされることもあります。
べき乗の定義
実数 \(n\) に対する \(a^n\) とは具体的にどういう意味なのでしょうか?
順を追ってみていきましょう。

自然数乗
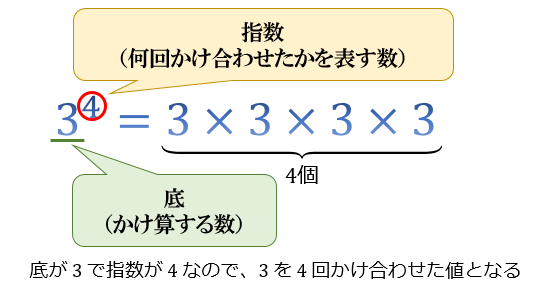
\(n\) が自然数(正の整数)のときの \(a^n\) は、「\(a\) を \(n\) 回かけ合わせた値」と定義されます。
0乗
\(n\) が \(0\) のときは、\(a^0=1\) と定義されます。
これは、「\(a\) を \(0\) 回かけ合わせた値」と考えると意味が分かりにくいですが、\(4\) 乗→\(3\) 乗→\(2\) 乗→\(1\) 乗と指数が \(1\) つ減るにつれて値が \(\frac{1}{a}\) 倍されている点に注目すると分かりやすいです。

\(a^0\) は「\(a^1\) の \(\frac{1}{a}\) 倍」と考えると \(a^0=a^1×\dfrac{1}{a}=1\) になりますね。
負の整数乗
\(n\) が負の整数のときは、\(a^n=\dfrac{1}{a^{-n}}\) と定義されます。
例えば \(a^{-2}=\dfrac{1}{a^{-1×(-2)}}=\dfrac{1}{a^2}\) となります。
こちらも、「\(a\) を \(-2\) 回かけ合わせた値」と考えると意味が分かりにくいですが、指数が \(1\) つ減るにつれて値が \(\dfrac{1}{a}\) 倍されているのに注目すると
\(a^{-1}=a^0×\dfrac{1}{a}=\dfrac{1}{a}\)
\(a^{-2}=a^{-1}×\dfrac{1}{a}=\dfrac{1}{a^2}\)
となるのが分かりますね。
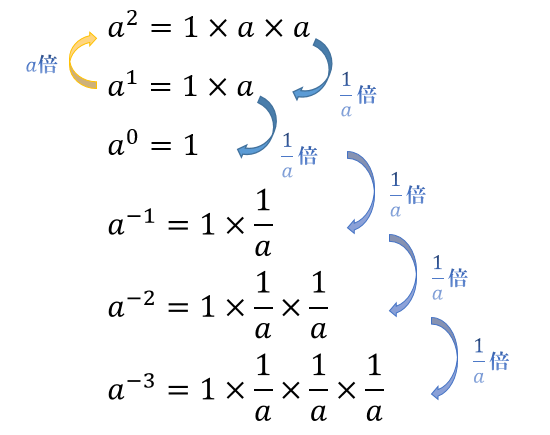
分数(有理数)乗
\(n\) が \(\frac{3}{10}\) のような分数(有理数)のときは、\(n=\frac{p}{q}\) に対し \(a^{\frac{p}{q}}=\sqrt[q]{a^p}\) と定義されます。
※ \(\sqrt[n]{x}\) は \(x\) の \(n\) 乗根
\(\sqrt[n]{x}=y\) ⇔ \(x=y^n\)
これは、\(a^2×a^3=a^{(2+3)}=a^5\) となる性質、つまり「累乗と累乗のかけ算」は「指数の足し算」になる性質を利用します。
この性質をべき乗 \(a^{\frac{1}{2}}\) に当てはめると、 \(a^{\frac{1}{2}}×a^{\frac{1}{2}}=a\) が成立。
ここから \(a^{\frac{1}{2}}\) は「\(2\) 乗したら \(a\) になる数」、すなわち \(a\) の平方根であることが分かります。

同じように、\(a^{\frac{3}{10}}\) は「\(10\) 乗したら \(a^3\) になる数 \(\sqrt[10]{a^3}\)」ですし
\(a^{1.73}\) は「\(100\) 乗したら \(a^{173}\) になる数 \(\sqrt[100]{a^{173}}\)」となります。
無理数乗
\(n\) が円周率 \(π≒3.14\) やネイピア数 \(e≒2.718\) 、2の平方根 \(\sqrt{2}≒1.414\) といった無理数の場合は、無理数のそばには必ず「非常に近い値の有理数」が存在することを利用します。
たとえば、\(2^π\) の場合。
\(3.14<π<3.15\) であることから \(2^{3.14}<2^π<2^{3.15}\) であることが分かりますよね。
ここで、より \(π\) に近い値を見ていくと \(3.141<π<3.142\) であることから、 \(2^{3.141}<2^π<2^{3.142}\) であることが分かります。
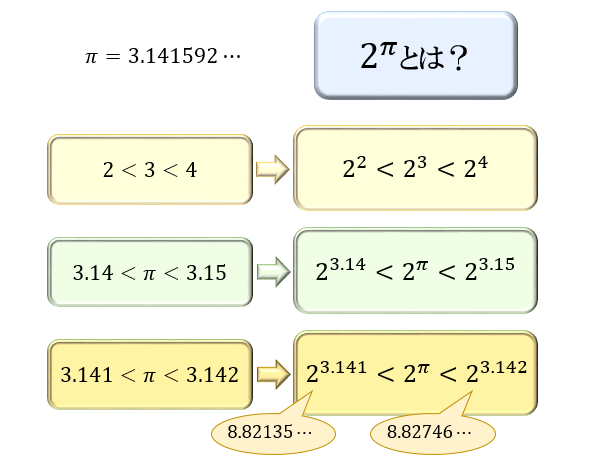
\(2^{3.14}≒8.821\) と \(2^{3.15}≒8.827\) から、\(2^π\) は約 \(8.82\) と判明。
ここからさらに \(2^{3.1415}<2^π<2^{3.1416}\) …と幅を狭めていったときの極限が、\(2^π\) の定義です。
実際に計算してみると、大体 \(2^π=8.824977827\cdots\) であることが分かります。