2つの三角形が相似であることを示すための条件を、三角形の相似条件と言います。
以下の3つの相似条件のうち、どれか1つでも成り立っているなら「それらの三角形は相似である」ということができます。
条件① 3つの辺の比がすべて等しい
条件② 2組の辺の比とその間の角がそれぞれ等しい
条件③ 2組の角がそれぞれ等しい
条件① 3つの辺の比がすべて等しい
3つの辺の比がすべて等しいとき「それらの三角形は相似である」ということができます。
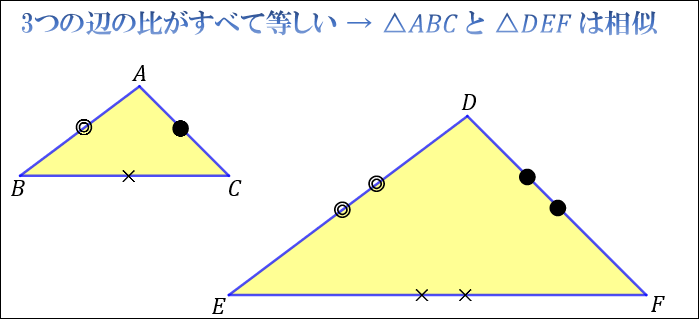
上図の場合、\(AB:BC:CA=DE:EF:FD=\) ◎:×:● より、相似となります。
この相似条件は、\(AB:DE=BC:EF=CA:FD\) と言いかえることもできます。
上図の場合、\(AB:DE=BC:EF=CA:FD=1:2\) より、相似となります。
条件② 2組の辺の比とその間の角がそれぞれ等しい
2組の辺の比が等しく、その間の角も等しいとき「それらの三角形は相似である」ということができます。
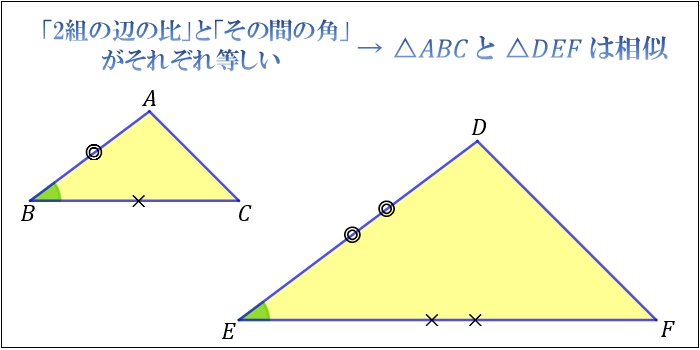
上図の場合、\(AB:DE=BC:EF=1:2\) かつ「その2辺の間の角」 \(∠B=∠E\) より、相似となります。
「その2辺の間の角」というのがポイントです。
条件③ 2組の角がそれぞれ等しい
2組の角がそれぞれ等しいとき「それらの三角形は相似である」ということができます。
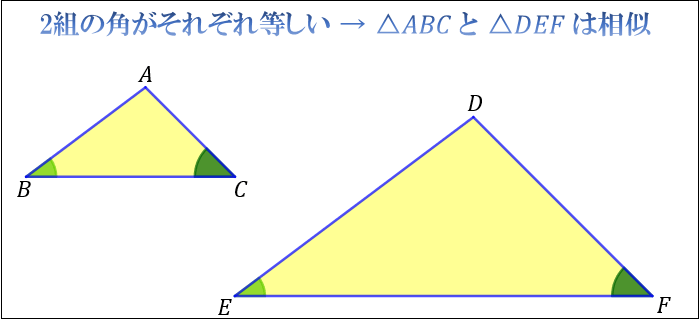
上図の場合、\(∠B=∠E\) かつ \(∠C=∠F\) より、相似となります。
相似条件を使った問題
【問1】:次の三角形 \(X,Y,Z\) のうち、\(A\) と相似な三角形を選んでください。
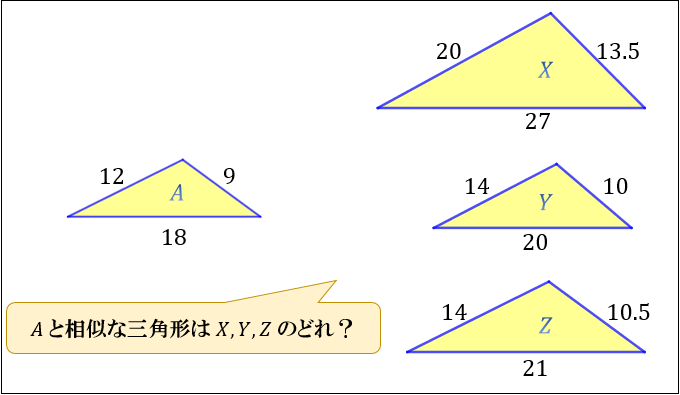
この問題では、「条件① 3つの辺の比がすべて等しい」を使います。
\(A\) の三角形の3辺の比は、小さい順に \(9:12:18=3:4:6\) です。
\(X,Y,Z\) の中で、3辺の比が \(3:4:6\) なのは \(Z\) の \(10.5:14:21\) だけ。

よって、\(A\) と相似な三角形は \(Z\) となります。
【問2】:下の図の線分 \(AD\) の長さを求めて下さい。
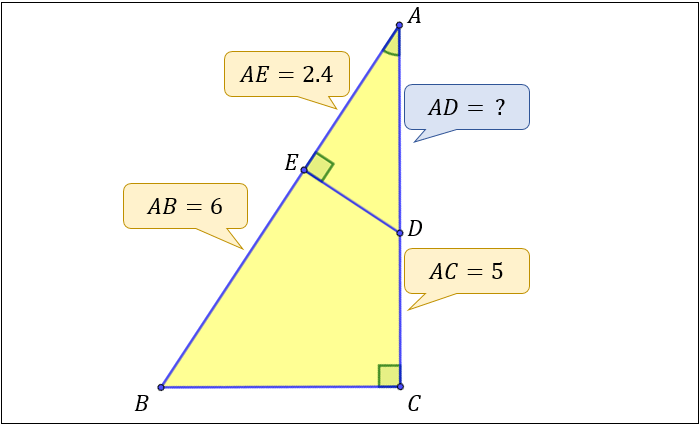
\(∠AED=∠ACB=90°\)
\(∠BAC=∠DAE\) (共通する角)
なので、「条件③ 2組の角がそれぞれ等しい」より
\(△BAC\) ∽ \(△DAE\) となります。
あとは、「相似な図形は対応する辺の比が等しい」ことを使うと
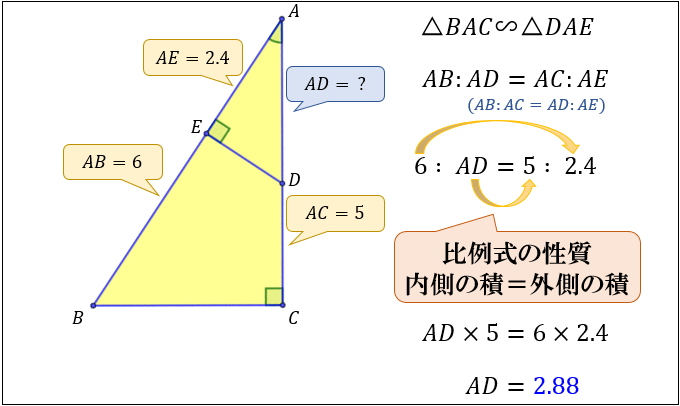
\(AD=2.88\) と求まります。