「同じ形のまま拡大・縮小した図形である」ことを、相似と言います。
たとえば、下図の三角形 \(DEF\) は「三角形 \(ABC\) の形を変えることなく \(\dfrac{1}{2}\) 倍に縮小した図形」です。
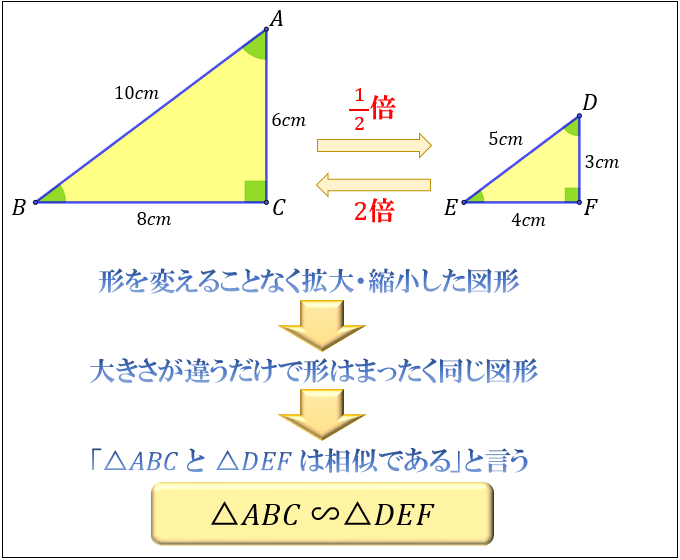
このように、大きさは違っても形がまったく同じ図形であるとき
「三角形 \(ABC\) と三角形 \(DEF\) は相似である」と言って
記号では「\(△ABC\) ∽ \(△DEF\) 」と書きます。
相似と合同とその書き方
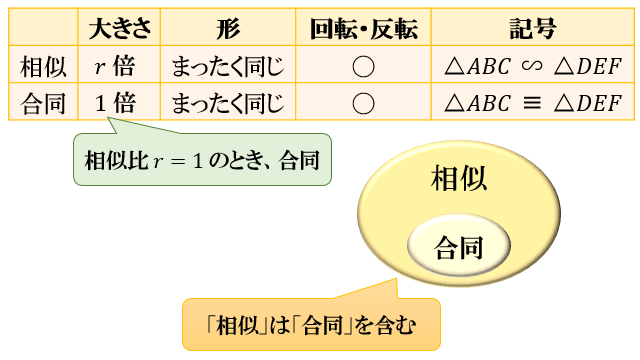
相似は、2つの図形の形がまったく同じであれば
何倍に拡大・縮小されていても相似ですし
回転・反転していても相似となります。
また、「相似」かつ「大きさも同じ(1倍)」のとき「2つの図形は合同である」と言います。
相似について記述するときは、対応している点の順番で書くのがポイントです。
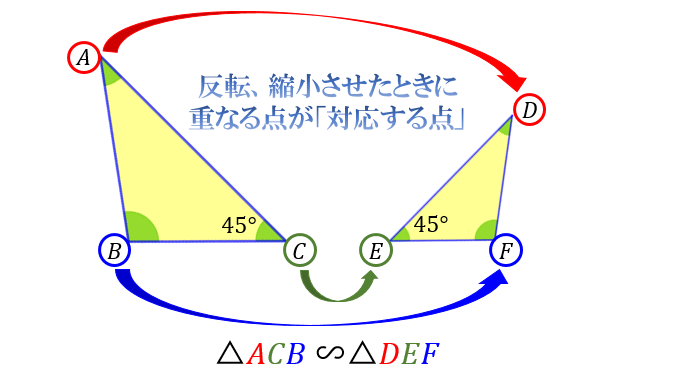
たとえば、下図の三角形 \(DEF\) は「三角形 \(ABC\) の形を変えることなく \(\dfrac{2}{3}\) 倍に縮小して、左右反転させた図形」なので、「2つの三角形は相似である」と言えます。
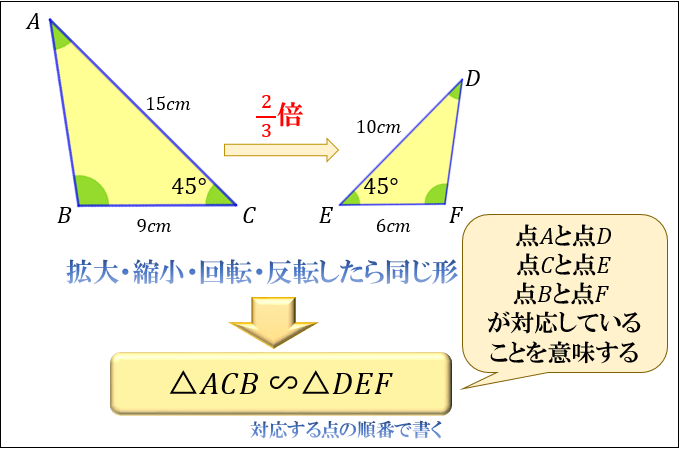
このとき、「点 \(A\) と点 \(D\) 」「点 \(C\) と点 \(E\) 」「点 \(B\) と点 \(F\) 」が対応していることを示すために
「\(△ACB\) ∽ \(△DEF\) 」
のように対応している点の順番で記述します。
対応している点どうしが同じ順番になってさえいればいいので
「 \(△ABC\) ∽ \(△DFE\) 」 や 「\(△CAB\) ∽ \(△EDF\)」
と書くこともできます。
相似な図形が持つ性質
相似な図形には
● 対応する線分の「長さの比」が、すべて等しい
● 対応する角の大きさが、それぞれ等しい
という2つの重要な性質があります。
対応する線分の「長さの比」が、すべて等しい
相似な図形は「同じ形のまま拡大・縮小した図形」なので、対応する線分の長さの比はすべて同じになります。
【例題】下図の2つの図形が相似であるとき、\(a\) , \(b\) はそれぞれ何cm?
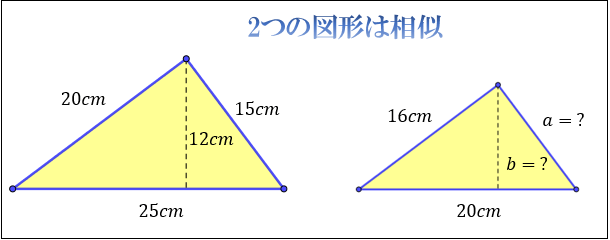
この問題の場合、右の図形は「左の図形の形を変えることなく \(\dfrac{4}{5}\) 倍に縮小した図形」になっています。
そのため、\(a,b\) はそれぞれ対応する線分 \(16\) cm, \(12\) cm の\(\dfrac{4}{5}\) 倍となります。
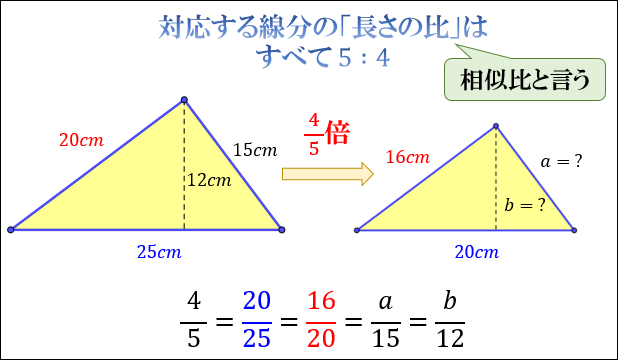
\(a=15×\dfrac{4}{5}=12\) cm
\(b=12×\dfrac{4}{5}=9.6\) cm
と求まります。
この「対応する線分の長さの比」のことを、相似比と言います。
対応する角の大きさが、それぞれ等しい
相似な図形は「同じ形のまま拡大・縮小した図形」なので、対応する角の大きさもそれぞれ等しくなります。
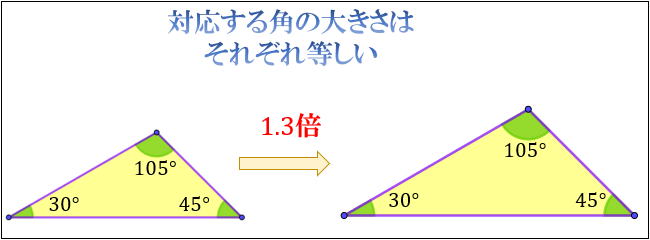
上図を見ると、相似な図形の3つの角の大きさはそれぞれ \(30°\)、\(45°\)、\(105°\) のままで変わっていないことが分かります。