正の整数 \(n\) に対して
「 \(1\) から \(n\) までの全ての整数をかけ算した値」のことを「 \(n\) の階乗」と言い、\(n!\) と書きます。

例えば
「 \(1\) の階乗」は \(1!=1\)
「 \(2\) の階乗」は \(2!=2×1=2\)
「 \(3\) の階乗」は \(3!=3×2×1=6\)
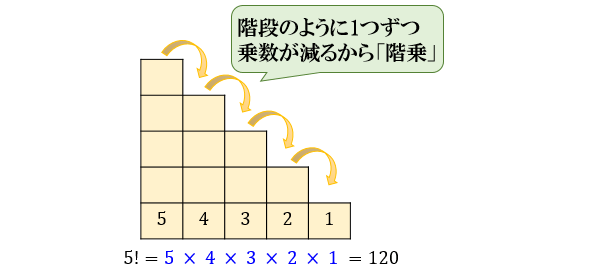
「 \(4\) の階乗」は \(4!=4×3×2×1=24\)
となります。
階段のように1つずつ乗数(かける数)が減っていくのが特徴的ですね。
階乗は、組み合わせの数やポアソン分布など、確率にまつわる様々な場面で登場する数です。
階乗を理解すれば「 \(A\) が \(B\) する確率は \(x\) %だ」と計算できるものがグッと増えてくるので、知らず知らずのうちに損な選択をしてしまうリスクが減ります。
ぜひ、このページで階乗の意味と性質を覚えていってください。
階乗の値一覧
階乗とは、\(1\) から \(n\) までの連続した \(n\) 個の整数をかけ算した値のことです。
また、「 \(0\) の階乗」は \(0!=1\) と定義されます。

「 \(0\) の階乗」から「 \(30\) の階乗」までの値は、以下のようになっています。

階乗の計算
さっそく、例題を解いてみましょう。
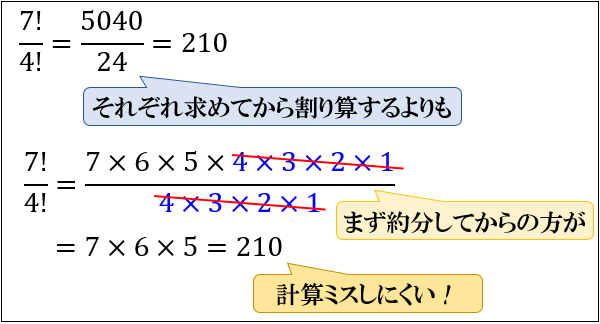
【問1】\(\dfrac{7!}{4!}\) を求めてください。
「 \(7\) の階乗」を「 \(4\) の階乗」で割った値を計算します。
この問題では、単純に「 \(7\) の階乗」と「 \(4\) の階乗」をそれぞれ求めてから割り算しても良いですが、階乗の共通する部分を先に約分しておくと計算量を格段に減らすことができます。
0の階乗が1になる理由
先に述べたように、「 \(0\) の階乗」は \(0!=1\) と定義されます。
「階乗が連続した整数のかけ算なら、\(0\) の階乗は \(0\) になるのでは?」と疑問に感じる方も少なくないと思いますが、これは階乗を並べて考えると分かりやすいです。
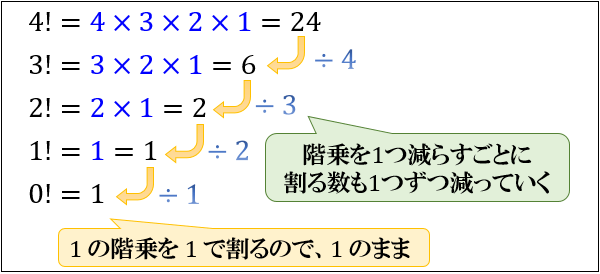
上図のように、「\(n\) の階乗は、\(n\) が \(1\) つ減るごとに割る数も \(1\) つずつ減っていく」という性質に着目すると、「\(0\) の階乗は \(1\) の階乗を \(1\) で割った値なので \(1\) 」と考えることができます。
また、\(n-1\) の階乗を \(n\) の階乗で割って \(n=1\) を代入した場合にも、\(0!=1\) が求められます。

以上のように、階乗の性質に矛盾することなく「 \(0\) の階乗」を定義するには、\(0!=1\) と定義する必要があるということですね。