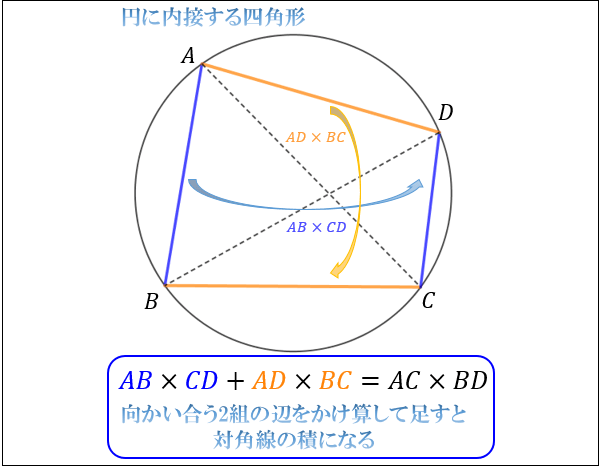
1つの円に2本の直線を引いたときに作られる「4つの線分の長さ」の間に、以下の等式が成り立つことを方べきの定理といいます。
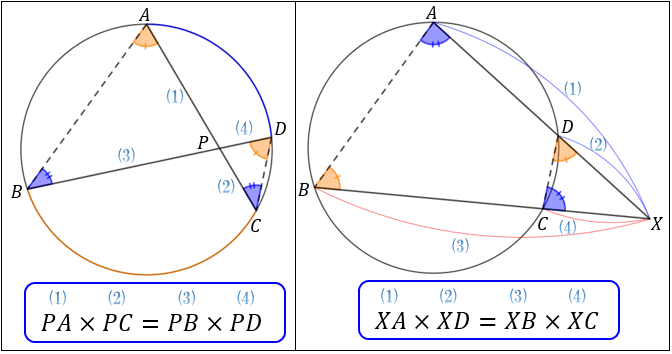
方べきの定理は、実生活では等式そのものよりも「円と直線の交点 \(A,B,C,D,P,X\) によって作られる2組の三角形がそれぞれ相似である」ということが重要な定理です。
「どの三角形とどの三角形が相似なのか?」「なぜ相似になるのか?」に注目しつつ、方べきの定理の証明を見ていきましょう。
方べきの定理その1
下図のように、円と2本の直線 \(AC,BD\) がある。
2本の直線の交点を \(P\) とすると
\(PA×PC=PB×PD\)
が成り立つ。
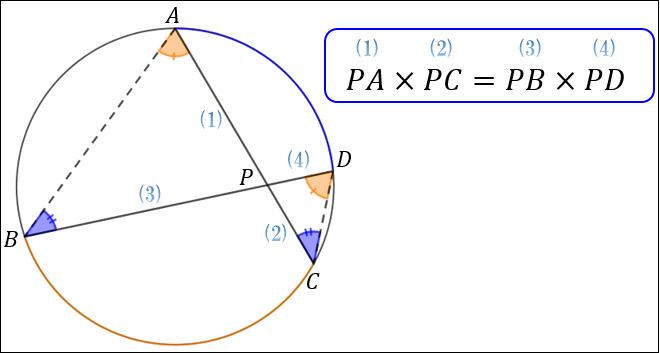
【証明】
まず円周角の定理より、同じ弧に対する円周角の大きさはそれぞれ等しくなります。
\(∠BAC\) と \(∠BDC\) はどちらも「弧 \(BC\) に対する円周角」なので \(∠BAC=∠BDC\)
\(∠ABD\) と \(∠ACD\) はどちらも「弧 \(AD\) に対する円周角」なので \(∠ABD=∠ACD\)
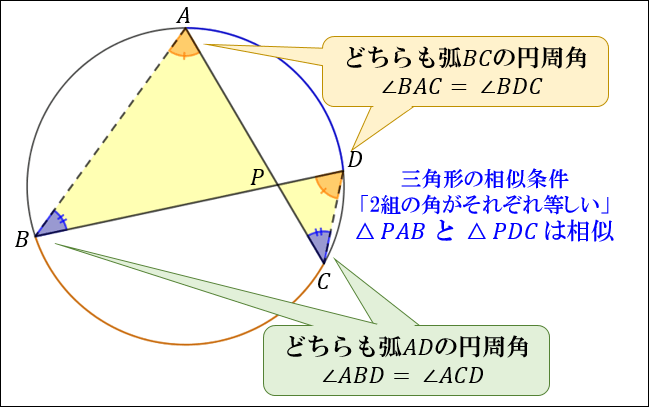
よって、三角形の相似条件「2組の角がそれぞれ等しい」を満たすことから
\(△PAB\) と \(△PDC\) は相似であることが分かります。
ここで、「相似な三角形の対応する辺の比は一定」という性質から
\(PA:PB=PD:PC\)
が成り立つので
\(PA×PC=PB×PD\)
が成り立つことが分かります。
方べきの定理その2
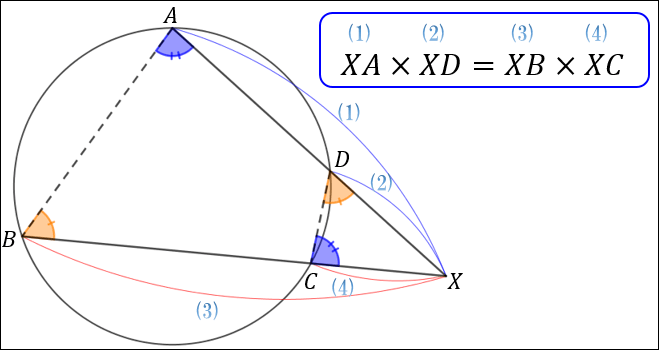
下図のように、円と2本の直線 \(AD,BC\) がある。
2本の直線の交点を \(X\) とすると
\(XA×XD=XB×XC\)
が成り立つ。
【証明】
四角形 \(ABCD\) の内角をそれぞれ \(∠A,∠B,∠C,∠D\) とおくと
\(∠A+∠C=180°\)、\(∠B+∠D=180°\) となります。
ここで「\(∠DCX\) は \(∠C\) の外角」「\(∠CDX\) は \(∠D\) の外角」なので
「内角と外角の和は180°」から
\(∠A=∠DCX(図の青い角)\)
\(∠B=∠CDX(図のオレンジの角)\)
となります。
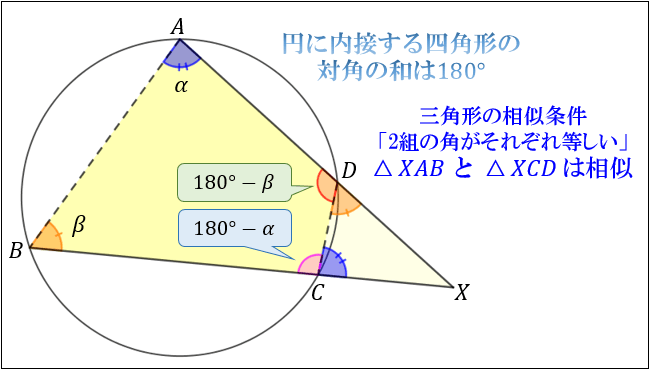
よって、三角形の相似条件「2組の角がそれぞれ等しい」を満たすことから
\(△XAB\) と \(△XCD\) は相似であることが分かります。
ここで、「相似な三角形の対応する辺の比は一定」という性質から
\(XA:XB=XC:XD\)
が成り立つので
\(XA×XD=XB×XC\)
が成り立つことが分かります。
方べきの定理その3
方べきの定理は、もう1パターンあります。
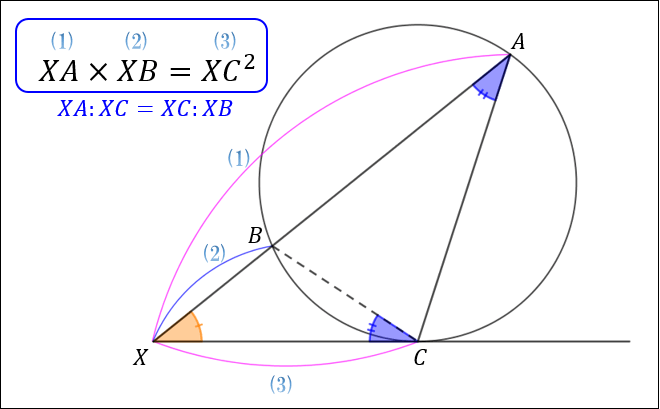
下図のように、円とその外側の点 \(X\) がある。
\(X\) から引いた円の接線の接点を \(C\) とし
\(X\) から円に引いた直線の2つの交点を \(A,B\) とすると
\(XA×XB={XC}^2\)
が成り立つ。
【証明】
接弦定理より「弦 \(BC\) に対する円周角」と「弦 \(BC\) と接線 \(XC\) がつくる角」は等しいので
\(∠A=∠BCX\) が成り立ちます。
また、\(∠AXC=∠CXB\) (共通する角)も成り立ちます。
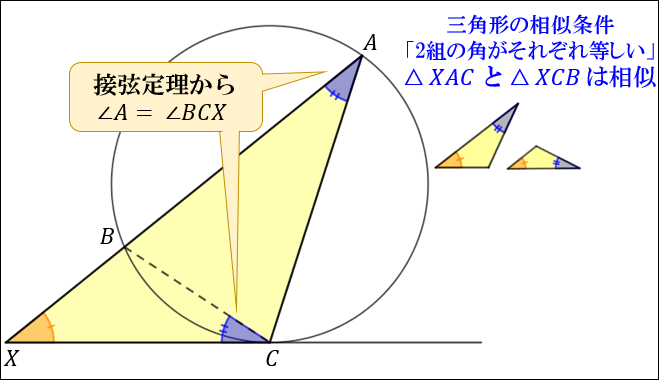
よって、三角形の相似条件「2組の角がそれぞれ等しい」を満たすことから
\(△XAC\) と \(△XCB\) は相似であることが分かります。
ここで、「相似な三角形の対応する辺の比は一定」という性質から
\(XA:XC=XC:XB\)
が成り立つので
\(XA×XB=XC×XC={XC}^2\)
が成り立つことが分かります。