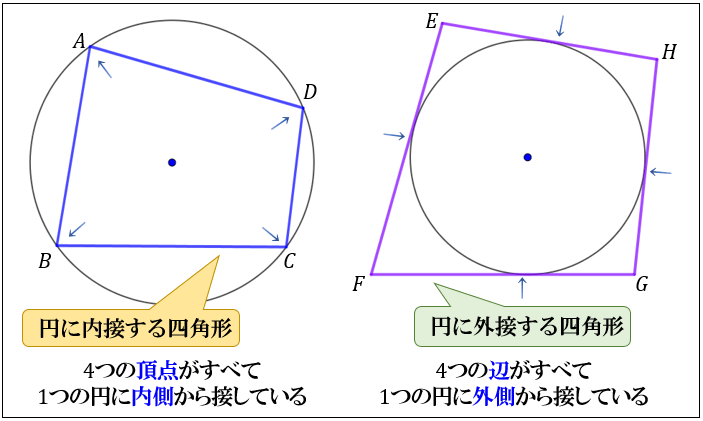
四角形の\(4\)つの頂点 \(A,B,C,D\) がすべて同じ円周上にある(内側から接している)とき、「四角形 \(ABCD\) は円に内接する」といいます。
反対に、四角形 \(EFGH\) の\(4\)つの辺がすべて同じ円に外側から接しているとき、「四角形 \(EFGH\) は円に外接する」といいます。
四角形 \(ABCD\) が円に内接していると、色んなことが分かります。
例えば、向かい合った角の和は \(180°\) になりますし、トレミーの定理と呼ばれる等式が成り立つという性質もあります。

このページでは、そんな「円に内接する四角形がもつ性質」をみていきましょう。
① 対角の和は180°
● 円に内接する四角形の対角の和は \(180°\)
● 円に内接する四角形の内角は、その対角の外角と等しい
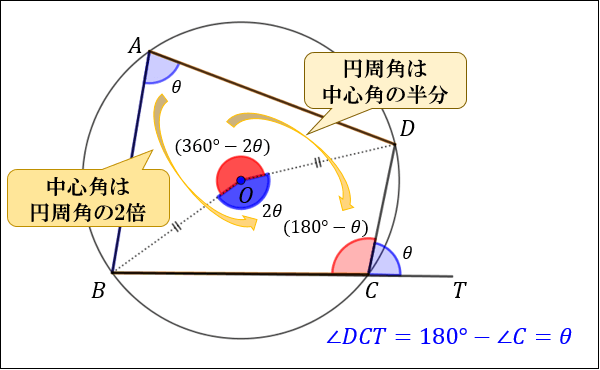
まず、円に内接する四角形では \(∠A+∠C=180°\) が成り立ちます。
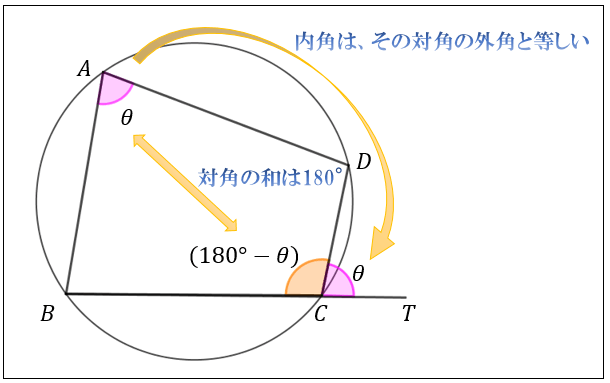
対角の和が \(180°\) になる理由は、円周角の定理から説明できます。
円の中心を点 \(O\) 、\(∠A=θ\) とおくと
円周角の定理より中心角は円周角の2倍なので、\(∠BOD(青)=2θ\)
次に、一周は \(360°\) であることから \(∠BOD(赤)=360°-2θ\)
円周角は中心角の半分なので、\(∠C=(360°-2θ)÷2=180°-θ\)
となり、\(∠A+∠C=180°\) であることが示されました。
② トレミーの定理
● \(AB×CD+AD×BC=AC×BD\)
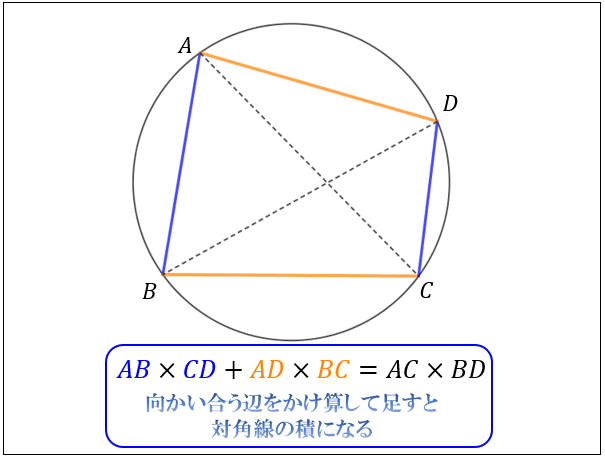
円に内接する四角形の向かい合う \(2\) 組の辺をそれぞれかけ算した合計が、対角線の積と一致するという定理です。
トレミーの定理は、長方形で考えると理解しやすくなります。
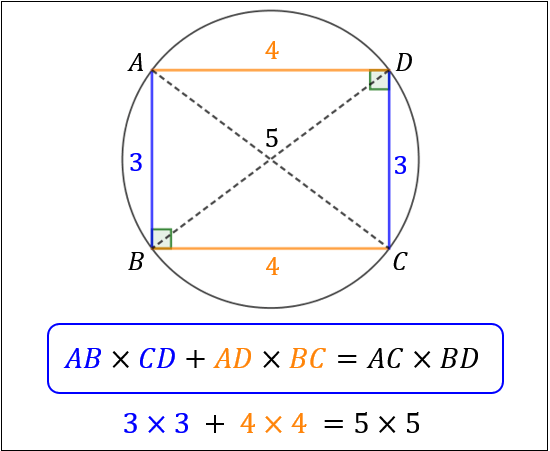
ちょうど、三平方の定理と同じ式になりますね。
③ 方べきの定理
四角形の対角線の交点を \(P\)、\(AD,BC\) の延長上の交点を \(X\) とおいたとき
● \(PA×PC=PB×PD\)
● \(XA×XD=XB×XC\)
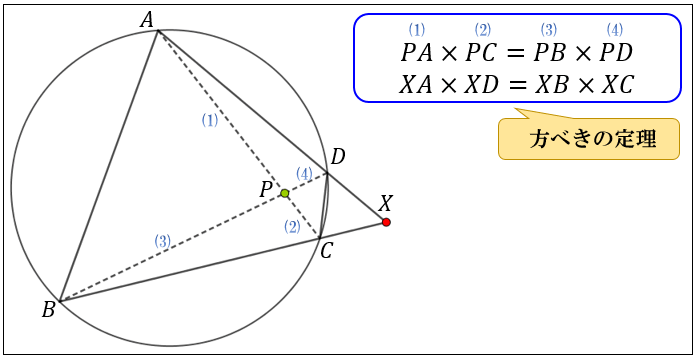
方べきの定理については、以下のページで詳しく解説しています。

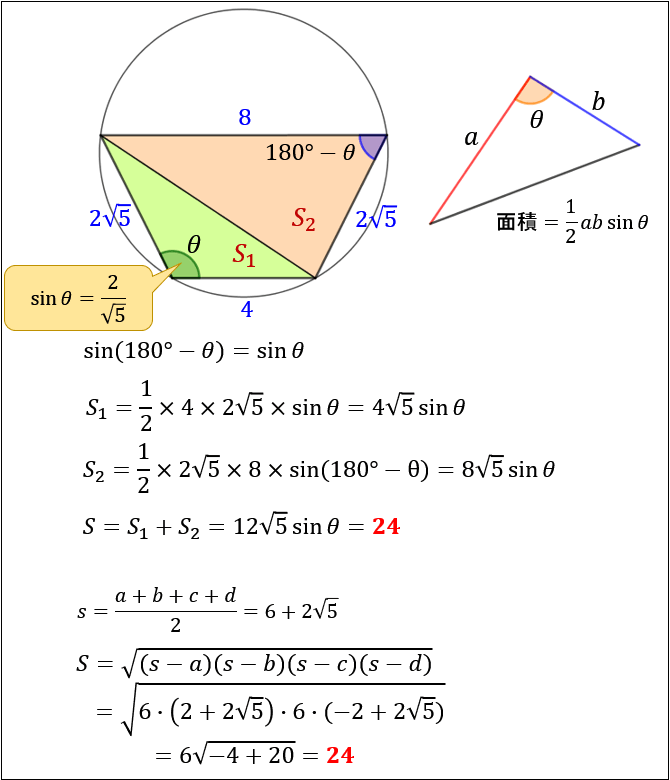
④ ブラーマグプタの公式
円に内接する四角形の \(4\) 辺の長さが \(a,b,c,d\) のとき
\(s=\dfrac{a+b+c+d}{2}\) とおくと
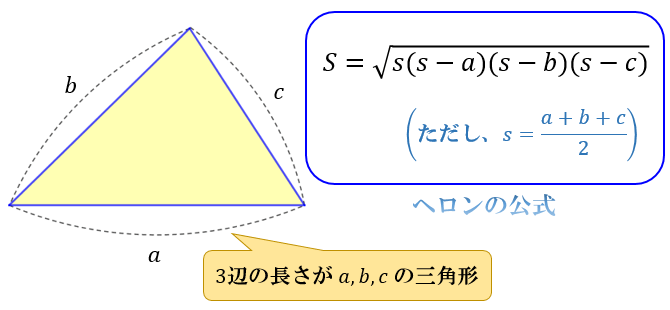
四角形の面積 \(S\) は \(S=\sqrt{(s-a)(s-b)(s-c)(s-d)}\) で表される
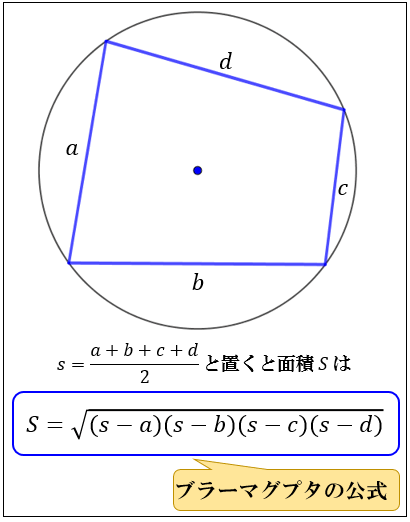
円に内接する四角形の面積は、三角形の面積の公式 \(\dfrac{1}{2}\sin{θ}\) を使って求めさせる問題が多いですが、このブラーマグプタ公式を覚えておくと素早く答えを出すことができます。