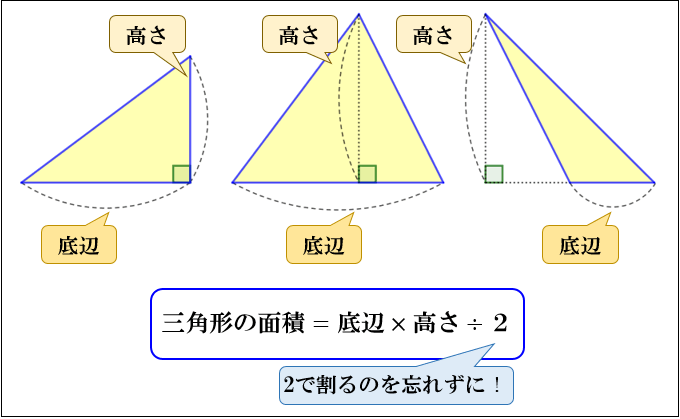
三角形の面積は
\(「三角形の面積=底辺×高さ÷2」\)
という公式から求めることができます。
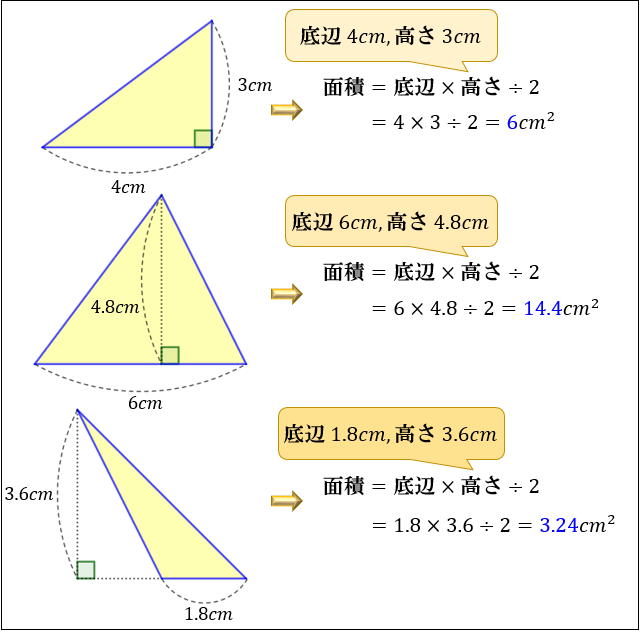
例題:底辺 \(4cm\)、高さ \(3cm\) の三角形の面積を求めてください
この問題では
公式 \(「三角形の面積=底辺×高さ÷2」\) に当てはめて
\(面積=4×3÷2=6cm^2\)
と求められます。
上図のようにどんな形をした三角形であっても、その面積は
公式 \(「三角形の面積=底辺×高さ÷2」\) で求まります。
このページでは、この公式の仕組みを図を使ってみていきましょう。
なぜ底辺×高さ÷2で求まるのか?
なぜ、どんな形をした三角形でも、その面積は \(「三角形の面積=底辺×高さ÷2」\) で求まるのでしょうか。
形がちがう2種類の「底辺 \(5cm\) 高さ \(2cm\) の三角形」を通じてみていきましょう。
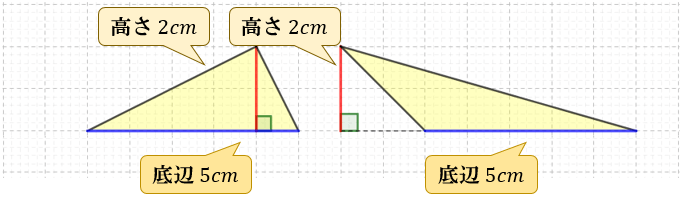
※1マス \(1cm\)
初めに、同じ形をした三角形をもう1つ用意します。
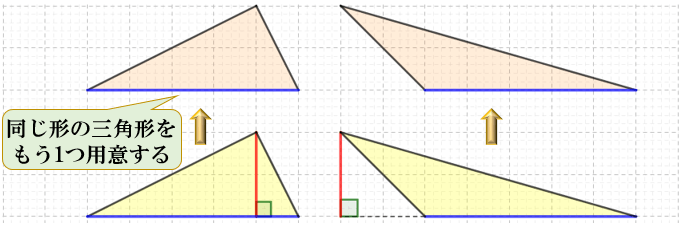
それをひっくり返して
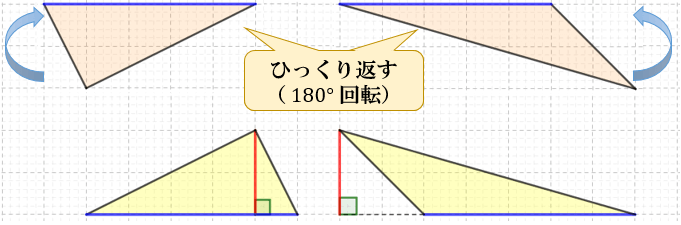
重ねると
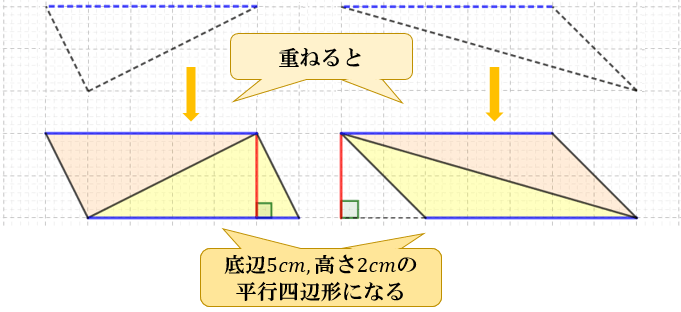
底辺 \(5cm\)、高さ \(2cm\) の平行四辺形になることが分かります。
ここで、平行四辺形の面積は
\(底辺×高さ\)
で求められます。
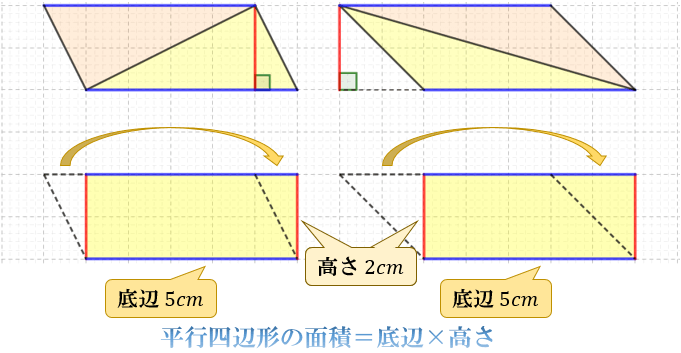
これは、上図のように平行四辺形の一部を切り取って右側に張り付けると
ちょうど \(1cm^2\) マス \(10\) 個分になることからも分かりますね。
よって
\(三角形2個分の面積=平行四辺形の面積\) と
\(平行四辺形の面積=底辺×高さ\)
から
\(「三角形2個分の面積=底辺×高さ」\) ということが分かります。
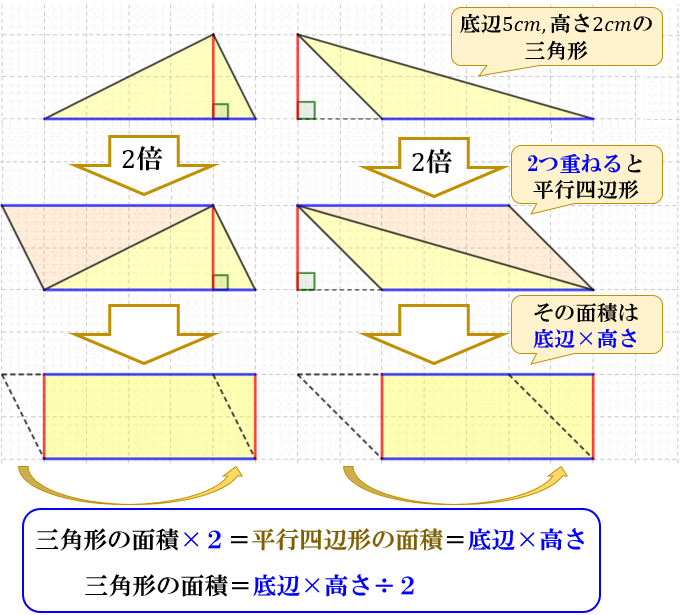
最後に
\(三角形2個分の面積=底辺×高さ\)
の式の両辺を2で割ると
\(「三角形の面積=底辺×高さ÷2」\)
となり、三角形の面積の公式が求められました。