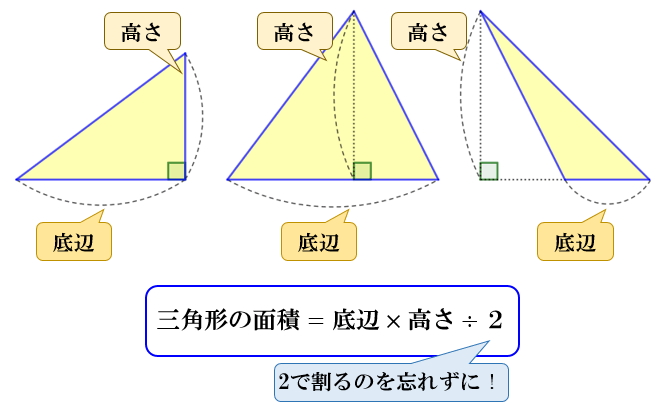
三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。
このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。
① 底辺×高さ÷2

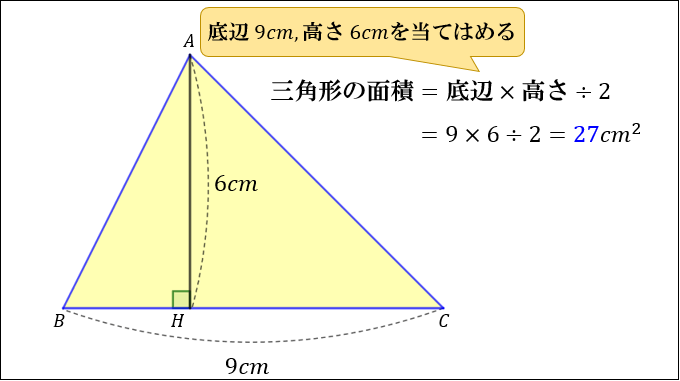
上図のような三角形 \(ABC\) があったとき、この三角形の面積は
\(「三角形の面積=底辺×高さ÷2」\)
で求められます。
たとえば、「底辺 \(9cm\) 高さ \(6cm\) の三角形」の面積は
\(9×6÷2=27cm^2\) となります。
なぜ \(底辺×高さ÷2\) で求まるのかについては「三角形の面積の求め方。なぜ底辺×高さ÷2で求まるのか?」で解説しています。
② 直角三角形・正三角形の性質を使って求める
「底辺 \(a\)、斜辺 \(c\) の直角三角形」や「1辺の長さ \(a\) の正三角形」は、高さ(下図の \(b,h\) ) の値がまだ分かっていなくても「三平方の定理」を用いることでその面積を求めることができます。
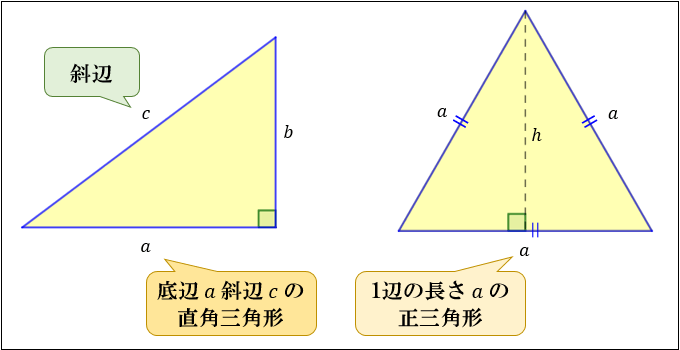
具体的には
「底辺 \(a\)、斜辺 \(c\) の直角三角形」の面積は \(S=\dfrac{1}{2}a\sqrt{c^2-a^2}\)
「1辺の長さ \(a\) の正三角形」の面積は \(S=\dfrac{\sqrt{3}}{4}a^2\)
で求められます。
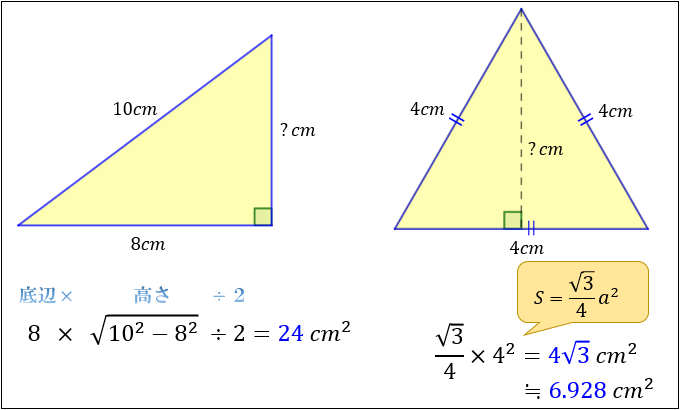
たとえば、「底辺 \(8cm\) 斜辺 \(10cm\) の三角形」の面積は
\(\dfrac{1}{2}×8×\sqrt{10^2-8^2}=24cm^2\)
「1辺の長さ \(4cm\) の正三角形」の面積は
\(\dfrac{\sqrt{3}}{4}×4^2=4\sqrt{3}cm^2\)
となります。
三平方の定理より
「底辺 \(a\)、斜辺 \(c\) の直角三角形」の高さは \(b=\sqrt{c^2-a^2}\)
「底辺 \(a\) の正三角形」の高さは \(h=\sqrt{a^2-(a/2)^2}=\dfrac{\sqrt{3}}{2}a\)
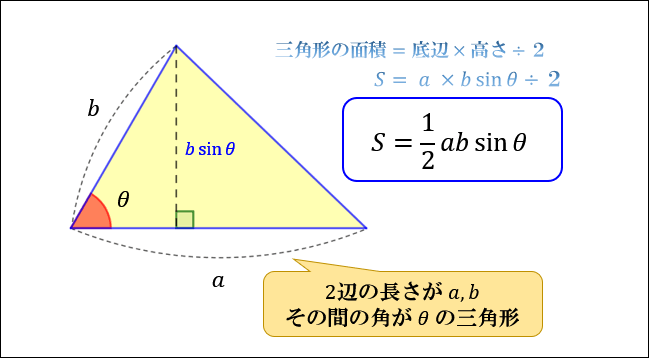
③ 2辺とその間の角の大きさを使った公式
2辺の長さ \(a,b\) とその間の角 \(θ\) が分かっている場合、その三角形の面積は
\(三角形の面積S=\dfrac{1}{2}ab \sin{θ}\)
で求められます。
たとえば、「2辺の長さが \(7,5\)、その間の角度が \(60°\) の三角形」の面積は
\(\sin{60°}=\dfrac{\sqrt{3}}{2}\) より
\(S=\dfrac{1}{2}×7×5×\sin{60°}=\dfrac{35\sqrt{3}}{4}\)
となります。

④ 3辺の長さから求める(ヘロンの公式)
3辺の長さ \(a,b,c\) が分かっている場合、その三角形の面積は
\(S=\sqrt{s(s-a)(s-b)(s-c)}\)
\(\left(ただし、s=\dfrac{a+b+c}{2}\right)\)
で求められます。

たとえば、「3辺の長さが \(7,6,5\) の三角形」の面積 \(S\) は
\(s=\dfrac{7+6+5}{2}=9\) から
\(S=\sqrt{9×(9-7)×(9-6)×(9-5)}\)
\(=6\sqrt{6}\)
となります。
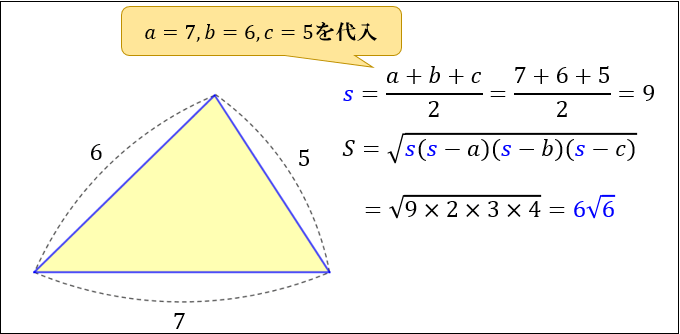
なぜこの公式で求まるのかについては「ヘロンの公式とは。図解でわかるその仕組みと証明方法」の記事を参考にしてみてください。
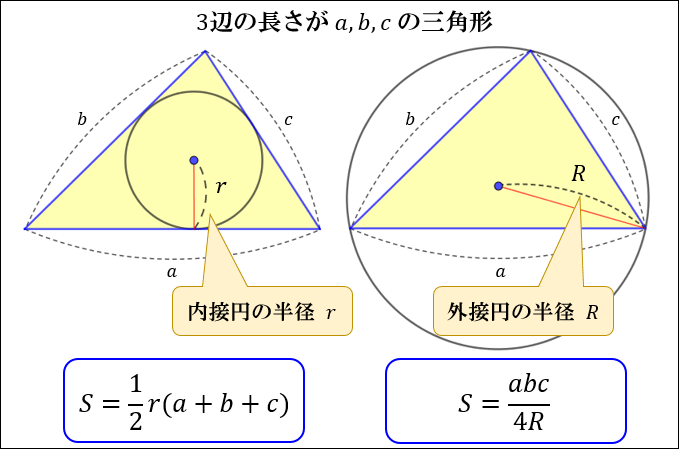
⑤ 内接円の半径・外接円の半径を使った公式
中学・高校数学では、計算がカンタンな「内接円の半径 \(r\) ・外接円の半径 \(R\) を使った公式」から面積を求めることもあります。
「3辺の長さ \(a,b,c\) 、内接円の半径 \(r\) の三角形」の面積は
\(S=\dfrac{1}{2}r(a+b+c)\)
「3辺の長さ \(a,b,c\) 、外接円の半径 \(R\) の三角形」の面積は
\(S=\dfrac{abc}{4R}\)
で求められます。
ただ、これらの公式を使わなくても3辺の長さ \(a,b,c\) の値が分かっている時点で「④ ヘロンの公式」を使えば三角形の面積を求めることは可能です。
【例題】3辺の長さが \(7,6,5\) の三角形があります。
この三角形の内接円の半径 \(r\) と外接円の半径 \(R\) を求めてください。
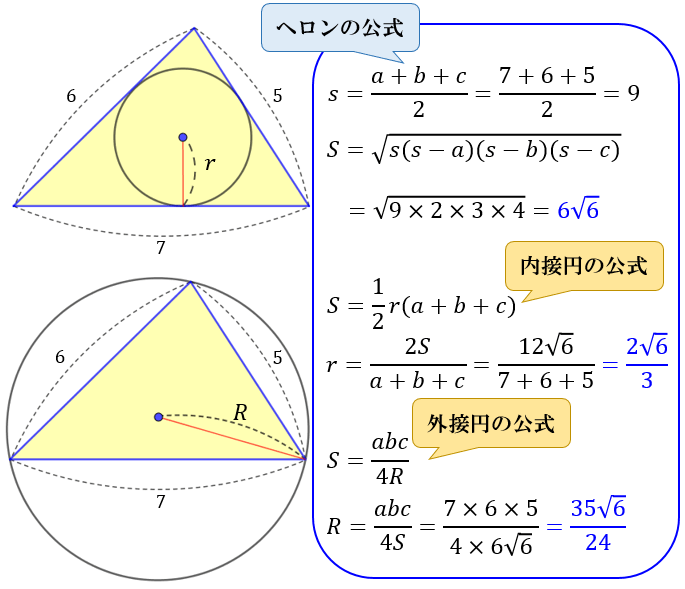
3つの公式を用いることで
内接円の半径 \(r=\dfrac{2\sqrt{6}}{3}\)
外接円の半径 \(R=\dfrac{35\sqrt{6}}{24}\)
が求まりました。