「\(P\) ならば \(Q\)」が成り立つとき、記号では\(「P→Q」\)と書き
\(Q\) は \(P\) であるための必要条件
\(P\) は \(Q\) であるための十分条件
といいます。
また、\(「P→Q」\)と\(「Q→P」\)の両方が成り立つとき
\(Q\) は \(P\) であるための必要十分条件
\(P\) は \(Q\) であるための必要十分条件
といいます。(「\(P\) と \(Q\) は同値である」ともいいます)
今回は、必要条件と十分条件の見分け方・覚え方について書いていきます。
必要条件と十分条件の見分け方
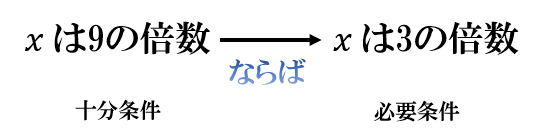
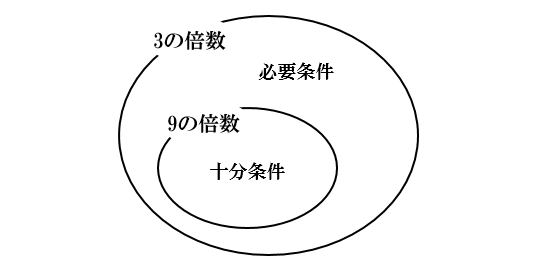
\(P:\)「\(x\) は \(9\) の倍数」
\(Q:\)「\(x\) は \(3\) の倍数」
これらの条件を満たす集合をそれぞれ図で表して、どちらが必要条件でどちらが十分条件か考えてみましょう。

● 「\(x\) は \(9\) の倍数」ならば「\(x\) は \(3\) の倍数」である
⇒ \(9\) の倍数なのに \(3\) の倍数ではない数は存在しない
● 「\(x\) は \(3\) の倍数」だからといって 「\(x\) は \(9\) の倍数」とは限らない
⇒ \(x=3,6,12\) などが反例として挙げられる
よって「\(x\) は \(9\) の倍数」→「\(x\) は \(3\) の倍数」が成り立つことから
● 「\(x\) は \(3\) の倍数」は(「\(x\) は \(9\) の倍数」であるための)必要条件である
● 「\(x\) は \(9\) の倍数」は(「\(x\) は \(3\) の倍数」であるための)十分条件である
となります。
「\(x\) は \(9\) の倍数」であるためには最低でも「\(x\) は \(3\) の倍数」という条件を満たす必要がある
「\(x\) は \(3\) の倍数」であるためには「\(x\) は \(9\) の倍数」という条件を満たせば十分だ
必要な条件=最低でも満たさないといけない条件=広めの条件
十分すぎる条件=厳しい条件=狭い条件
と考えると分かりやすいです。
覚え方
必要条件・十分条件の覚え方は色々ありますが、特にシンプルで覚えやすいのは
十分条件の「十」・必要条件の「要」に注目する方法です。
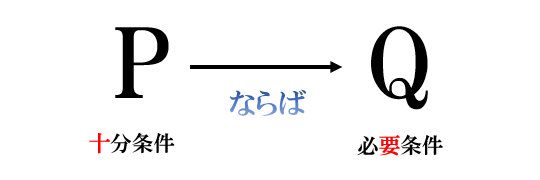
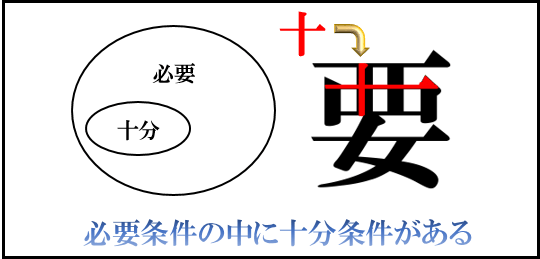
矢印を使って覚えるときは、「十→要」で『重要』と覚えます。

図を使って覚えるときは、「要」という漢字の中に「十」があることに注目して
『必要条件の中に十分条件がある』と覚えます。
必要条件・十分条件の判別問題
以下の( )の中に(必要・十分・必要十分)の3つのうち最も適切なものを入れてください。ただし \(x,y\) は実数とします。
問1:「\(x=2\) かつ \(y=2\)」は「\(xy=4\)」であるための( )条件である
問2:「\(x^2>25\)」は「\(x>5\)」であるための( )条件である
問3:「\(x+y=0\) かつ \(xy=0\)」は「\(x=0\) かつ \(y=0\)」であるための( )条件である
問1解答
「\(x=2\) かつ \(y=2\)」ならば「\(xy=4\)」である
「\(xy=4\)」だからといって「\(x=2\) かつ \(y=2\)」とは限らない。反例:\(x=ー2\) かつ \(y=ー2\)
よって「\(x=2\) かつ \(y=2\)」は「\(xy=4\)」であるための十分条件である
問2解答
「\(x^2>25\)」だからといって「\(x>5\)」とは限らない。反例:\(x<ー5\)
「\(x>5\)」ならば「\(x^2>25\)」である
よって「\(x^2>25\)」は「\(x>5\)」であるための必要条件である
問3解答
「\(x+y=0\) かつ \(xy=0\)」ならば「\(x=0\) かつ \(y=0\)」である
「\(x=0\) かつ \(y=0\)」ならば「\(x+y=0\) かつ \(xy=0\)」である
よって「\(x+y=0\) かつ \(xy=0\)」は「\(x=0\) かつ \(y=0\)」であるための必要十分条件である