微分係数と導関数の違いとその使い分け

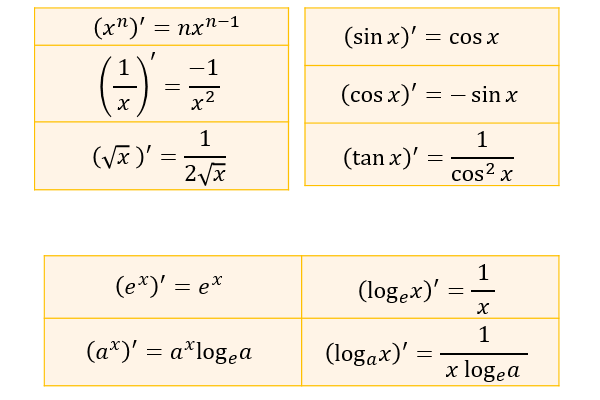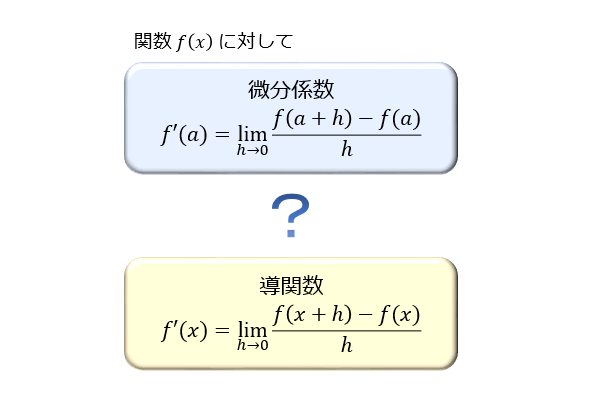
微分の勉強をするときに混同してしまいやすい2つの数。微分係数と導関数。

微分係数と導関数はその定義式がよく似ているので「なぜ使い分けるのか」「どう使い分けるのか」が分かりにくいという人も多いのではないでしょうか。

実は、微分係数と導関数には「定数なのか、関数なのか」という違いがあります。

今回は「定数・関数・変数」の意味も踏まえつつ、その違いを見ていきましょう。

微分係数とは

関数 \(f(x)\) と定数 \(a\) に対して、\(x=a\) における微分係数 \(f'(a)\) は次の式で定義されます。

$\displaystyle f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h} $

$\displaystyle f'(3)=\lim_{h \to 0}\frac{f(3+h)-f(3)}{h} $

$\displaystyle =\lim_{h \to 0}\frac{(3+h)^2-3^2}{h}=\lim_{h \to 0}\frac{6h+h^2}{h} $

$\displaystyle =\lim_{h \to 0}(6+h)=6 $

導関数とは

関数 \(f(x)\) に対して、導関数 \(f'(x)\) は次の式で定義されます。

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} $ 

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} $

$\displaystyle =\lim_{h \to 0}\frac{(x+h)^2-x^2}{h}=\lim_{h \to 0}\frac{2xh+h^2}{h} $

$\displaystyle =\lim_{h \to 0}(2x+h)=2x $

定数と関数

微分係数と導関数の違いは、「定数・関数・変数」を理解するとわかります。

定数 \(a\) とは、特定の数字の代わりに文字を使っているだけで \(1\) や \(3\) と同じ固定された値のこと。

変数 \(x\) とは、一定の範囲内の任意の値をとる数のこと。

関数 \(f(x)\) は「変数 \(x\) によって値が決まる数」ということを意味しています。

このように、定数と変数は意味合いが異なるので、定数 \(a\) を用いた \(f'(a)\) と変数 \(x\) を用いた \(f'(x)\) では意味合いが変わってくるのです。

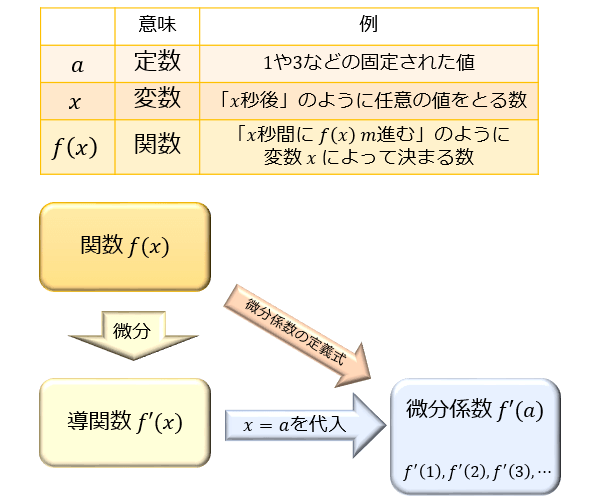
微分係数は、問１のように関数 \(f(x)\) を微分係数の定義式に当てはめて求めることもできますが、以下のように微分の公式から \(f'(x)\) を求めて、\(x=a\) を代入して求めることもできます。

\(f(x)=x^n\) の微分の公式は \(f'(x)=nx^{n-1}\) より、\(f(x)=x^2\) を微分すると \(f'(x)=2x\)

\(x=3\) を代入して、\(f'(3)=6\)

この求め方のほうが楽なので、微分に慣れたらこちらの求め方を使うようにしましょう。

具体的な使い分け

微分係数は「特定の点における \(y=f(x)\) の傾き」に相当し

導関数は「すべての点における \(y=f(x)\) の傾きを \(x\) の関数として表したもの」に相当します。

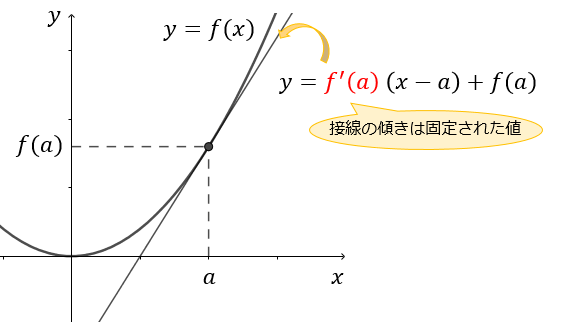
例えば、特定の点における接線の傾きには導関数 \(f'(x)\) ではなく微分係数 \(f'(a)\) を使わなければなりません。

逆に、第2次微分係数 \(f^{\prime\prime}(a)\) を求めたいときは導関数 \(f'(x)\) を微分してから \(x=a\) を代入する必要があります。

微分係数は定数なので、\(f'(a)\) を \(x\) で微分すると \(0\) になってしまうからです。

Tooda Yuuto

導関数は「元となる関数 \(f(x)\) を微分することで導き出される別の関数」

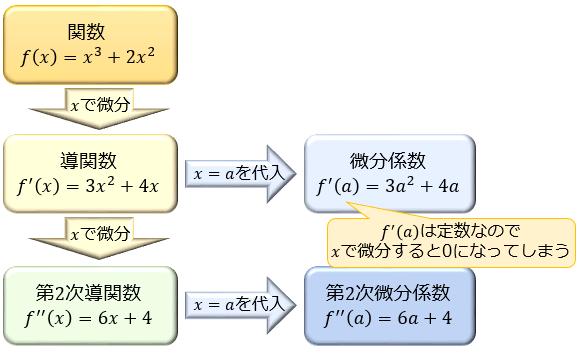
微分係数は「導関数 \(f'(x)\) の \(x\) に特定の値を代入することで得られる定数で、微分係数の定義式から直接求めることもできる」

とおさえておくと分かりやすいと思います。