2つのベクトルに対して、以下の式で表される値をベクトルの外積と言います。

外積は「ベクトル積」(英語で vector product)とも呼ばれる
たとえば、\((1,2,3)\) と \((4,5,6)\) の外積は、\((-3,6,-3)\) となります。
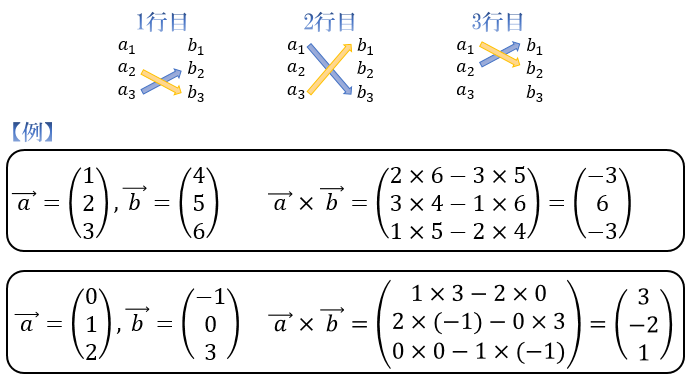
このページでは、外積の定義や性質を見ていきましょう。
外積の定義
外積 \(\vec{\ a\ }×\vec{\ b\ }\) とは
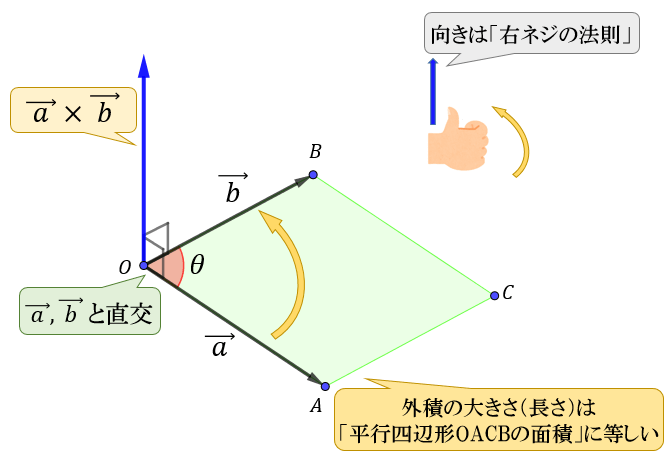
①その向きが \(\vec{\ a\ }\) と \(\vec{\ b\ }\) に直交する方向で(右ネジの法則)
②その長さが「\(\vec{\ a\ }\) と \(\vec{\ b\ }\) を2辺とする平行四辺形の面積」に等しい
という性質を持ったベクトルのことを言います。
外積はもとのベクトルと直角に交わる
外積 \(\vec{\ a\ }×\vec{\ b\ }\) は、元となったベクトル \(\vec{\ a\ },\vec{\ b\ }\) の両方と直角に交わるという性質を持っています。
そのため、2つのベクトル \(\vec{\ a\ },\vec{\ b\ }\) が与えられたときに、それらの両方と直角に交わるベクトルを求めたい場合、外積を計算すると便利です。

外積と元のベクトルが直角に交わることは、それらの内積が \(0\) になることから示せる。
\(\vec{\ a\ }\cdot\vec{\ b\ }=|\vec{\ a\ }||\vec{\ b\ }|\cos{θ}\) より
\(\vec{\ a\ }\cdot\vec{\ b\ }=0\) ⇔ \(\cos{θ}=0,\) \(θ=90°\) となるため
外積の大きさは平行四辺形の面積と等しい
外積の大きさ \(|\vec{\ a\ }×\vec{\ b\ }|\) は、元となったベクトル \(\vec{\ a\ },\vec{\ b\ }\) によって作られる平行四辺形の面積 \(|\vec{\ a\ }||\vec{\ b\ }|\sin{θ}\) と等しくなります。
\(|\vec{\ a\ }×\vec{\ b\ }|=|\vec{\ a\ }||\vec{\ b\ }|\sin{θ}\)
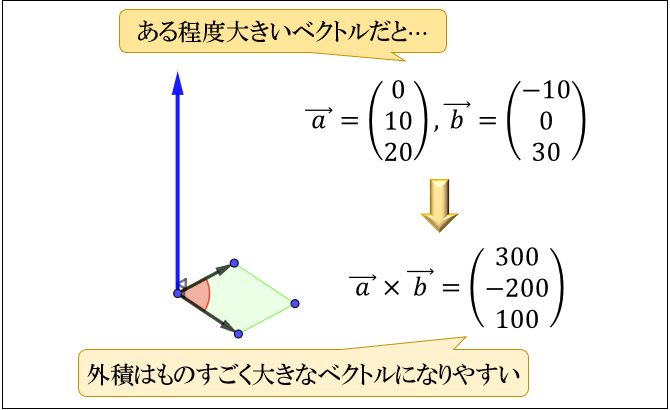
そのため、元となったベクトル \(\vec{\ a\ },\vec{\ b\ }\) がある程度大きなベクトルの場合、外積はものすごく大きなベクトルになりやすいという特徴があります。