「2」を3回かけ算すると、2×2×2=8になりますよね。
これを「2を3乗したら8になる」と言い、以下のように書きます。

このとき、「2」の右上に乗っている「3」のことを「指数」と言います。
指数は「1つの数を何回かけるか」を表しています。
一方、「〇を何乗すれば△になるか」を表す数のことを「対数」と言います。
例えば「2を何乗すれば8になるか」を表す数は以下のように表記され、
これを「2を底とする8の対数」と言います。

「2を底とする8の対数」は3
「3を底とする 81 の対数」は4
「5を底とする 1/25 の対数」は-2
という具合ですね。
今回は、そんな対数とその有用性について書いていきます。
photo credit:Eric Vanderpool
指数・対数・底・真数
さきほどの指数と対数の意味を聞いて、「あれ?指数と対数って似てるというか、実質的に同じじゃない?」と少し困惑した人もいるかもしれません。
そう、実は「指数」と「対数」は同じ数のことを指しているんです。
ただ、その視点・使い方が異なるため、同じ数に対して違う名前がついています。
まず \(a^x=b\) のとき、\(x\) のことを指数と言います。
指数は、主に「\(a\) を \(x\) 乗したらいくつになるか?」を考えるときに使います。
これに対し \(x=\log_{a}b\) のとき、\(x\) のことを対数と言います。
対数は、主に「\(a\) を何乗したら \(b\) になるか?」を考えるときに使います。
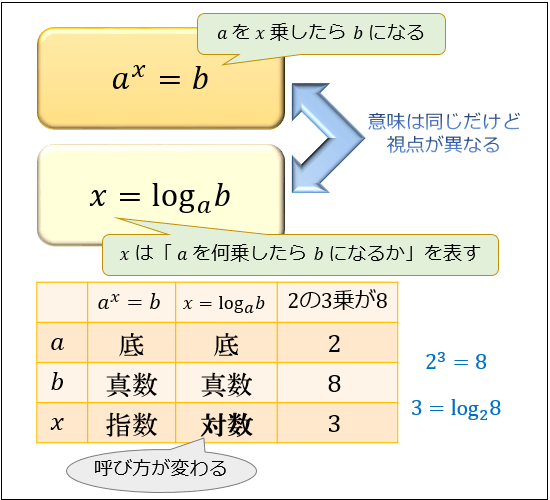
\(a^x\) の形のときは、 \(a\) の右上に乗っている \(x\) のことを「指数」
\(\log_ab\) の形のときは、\(x=\log_{a}b\) ことを「\(a\) を底とする \(b\) の対数」と呼ぶ
とおさえておきましょう。
ちなみに、\(\log_ab\) という形における \(a\) のことを底、\(b\) のことを真数と言います。
定義:\(a>0,a\neq1\)のとき、\(b>0\) に対して \(a^x=b\) を満たす \(x\) がただ1つ定まる。この \(x\) を「\(a\) を底とする \(b\) の対数」と言い、\(\log_{a}b\) と書く
対数の公式。真数のかけ算が対数の足し算に
対数には、計算でよく使う公式がいくつかあります。
ここでは、その中でも特によく使う3つを紹介します。
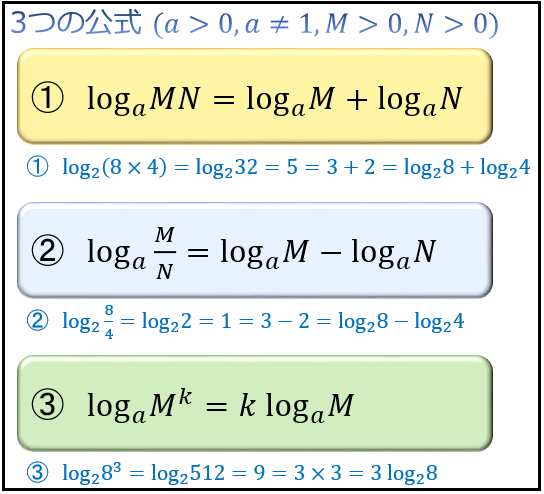
「真数のかけ算」が「対数の足し算」
「真数の割り算」が「対数の引き算」
「真数の累乗」が「対数のかけ算」
になっているのが分かりますね。
対数をとるとはどういう意味?
様々なデータを測って分析をする際、「対数をとる」と非常に便利なことが多いです。
「対数をとる」とは、\(M^k=N\ (>0)\) が成り立つときには \(\log_{a}M^k=\log_{a}N\) も成り立つことを利用して、式の形を \(\log_aM^k=\log_aN\) に変形することを言います。
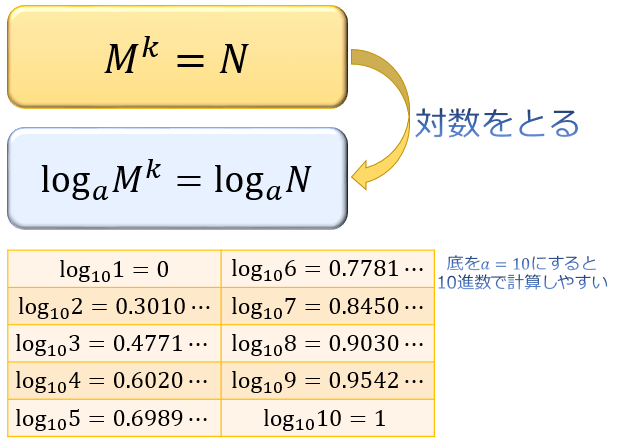
たとえば、\(2^5=32\) ⇒ \(\log_{10}2^5=\log_{10}32\) といった感じですね。
底 \(a\) は「\(a>0,a\neq1\)」なら何でもいいのですが
① 10進数で計算する時に便利な \(10\)
② 微分するときに便利なネイピア数 \(e=2.718\cdots\)
のどちらかで対数をとるのが基本です。
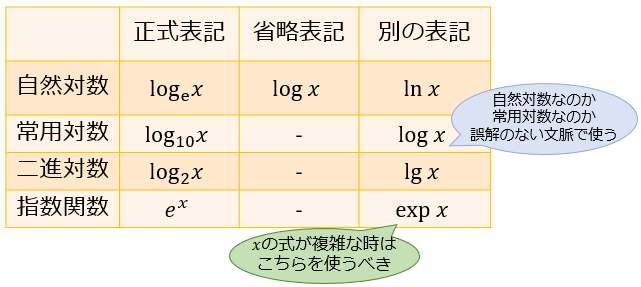
\(10\) を底とする対数は常用対数。ネイピア数 \(e\) を底とする対数は自然対数といいます。
対数をとるメリット
では、対数をとるとどんなメリットがあるのか?
その答えの1つは「かけ算を足し算に、累乗をかけ算に落としこみ、計算を簡単にできる」ことにあります。
たとえば、皆さんは「\(2^{100}\) は何桁の数で、上 \(3\) 桁の数字はいくつか?」という問題が出たら、どうやって答えを求めるでしょうか?
電卓を使おうにも、数が膨大過ぎて電卓の桁数では全く足りませんよね。

一方、\(Z=2^{100}\) とおいて対数をとると、以下のように簡単なかけ算によって、\(Z≒10^{30.103}\) で表せることが分かります。
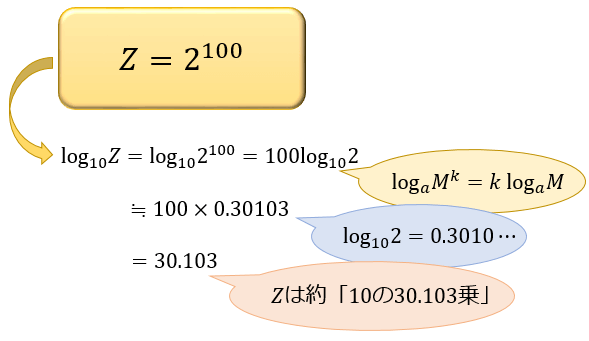
\(10^1\leq y<10^2\) は \(2\) 桁の数
\(10^2\leq y<10^3\) は \(3\) 桁の数
\(10^n\leq y<10^{n+1}\) は \(n+1\) 桁の数
つまり、\(10^{30}\leq Z<10^{31}\) は \(31\) 桁の数であることから
\(2^{100}≒10^{30.103}\) は \(31\) 桁の数であると分かります。
あとは、常用対数表から \(1.26\leq10^{0.103}<1.27\cdots\) であることを読み取れば、
\(2^{100}\) の上 \(3\) 桁の数字が \(126\) であることも分かります。
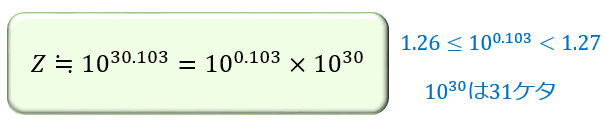
答え:「\(2^{100}\) は \(31\) 桁の数であり、上 \(3\) 桁の数字は \(126\) である」
以上のように、対数を使うと累乗の計算がすごく楽になる、というわけです。
\(10^{0.103}\) :\(1000\) 乗したときに \(10^{103}\) と等しくなる値
他にも「10年で \(+200\) %の経済成長を見込むには、何年で \(+100\) %の経済成長をする必要があるか?」といった経済学的な問題においても、対数が役に立ってきますよ。

対数は、知れば知るほどその有用性を実感できる、とても便利な考え方です。
いろんなデータを分析するときに、ぜひ活用してください!
常用対数と自然対数の使い分けについては、以下の記事も参考にしてみてください