
回帰分析とは、説明変数 \(x\) によって目的変数 \(y\) の変動を \(y=f(x)\) の形でどの程度説明できるのかを分析する手法です。
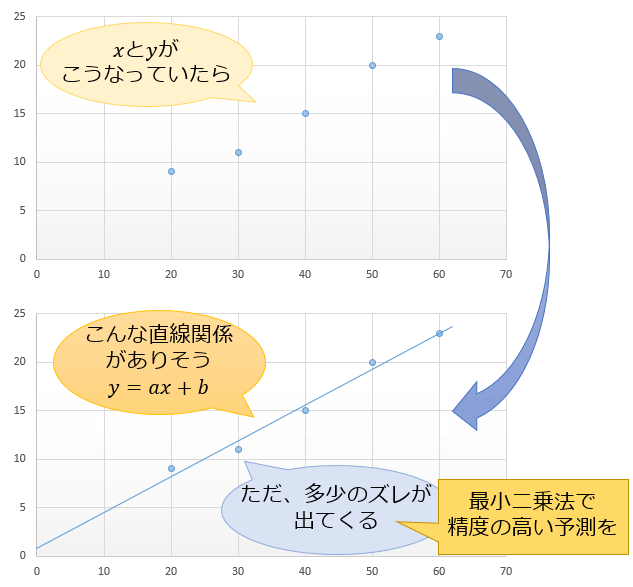
回帰分析の中で最もシンプルなのが \(y=ax+b\) に関する最小二乗法。
この手法は「部屋の広さと家賃の関係」を調べたいときなど、様々な場面で使うことができます。(詳しくは下記記事を参考に)
一方、経済学や自然科学では各変数を対数変換した \(\log_{e}y=A\ \log_{e}x+B\) の形で最小二乗法を使っていることが少なくありません。
何の前触れもなく登場することから、「なんで回帰分析で対数が出てくるんだろう?」と疑問に思う方も多い箇所だと思います。
そこで今回は、回帰分析において対数変換を行う意味・前提条件などについて書いていきます。
photo credit:Francisco Osorio
「対数変換する・しない」で異なる分析結果に
対数変換とは、「対数をとる」とほとんど同じ意味の言葉です。
回帰分析の文脈では、変数 \(x\) を自然対数 \(\log_{e}x\) に変換することを指します。
具体的に、説明変数 \(x\) と目的変数 \(y\) の間に以下の関係があった場合を考えてみましょう。

対数変換しない場合
まずは普通に、\(y=ax+b\) について最小二乗法で解いてみます。
すると、以下の回帰式が求められます。(計算方法は最小二乗法の記事を参照)

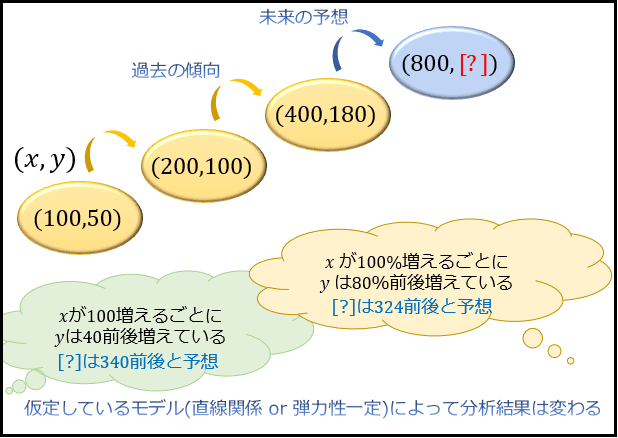
この回帰式においては、例えば \(x=800\) では \(y=0.4×800+14=334\) と予測されることになります。
対数変換した場合
一方、説明変数 \(x\) と目的変数 \(y\) を対数変換した場合。

(\(e≒2.718\) はネイピア数)
これを、\(\log_{e}y=A\ \log_{e}x+B\) について最小二乗法で解くと、以下の回帰式が求められます。
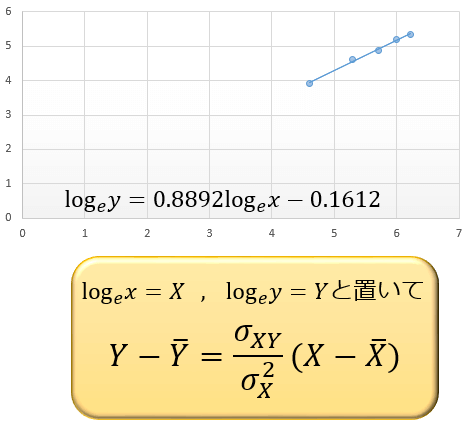
この回帰式においては、\(x=800\) では \(\log_{e}y=0.8892×\log_{e}800-0.1612≒ 5.78\) より \(y≒e^{5.78}≒324\) と予測されることになります。
「対数変換をする・しない」で分析結果が異なることが分かりますね。
直線関係モデルと弾力性一定モデル
\(y=ax+b\) について解いた最小二乗法は「\(x\) が増減した量に比例して \(y\) も増減する」という直線関係のモデルを仮定して予測・説明を行っています。
これに対して、対数変換をしてから \(\log_{e}y=A\ \log_{e}x+B\) について解いた最小二乗法は「弾力性が一定である」というモデルを仮定して予測・説明を行っています。
弾力性とは、経済学用語の1つで「\(x\) の変化率に対する \(y\) の変化率の比」のことです。
(例)所得 \(x\) が \(1\)% 増えたら需要 \(y\) が \(0.8\)% 増える場合、需要の所得弾力性は \(0.8\) となる
下の式を見ればわかる通り \(A=(dy/y)/(dx/x)\)、つまり係数 \(A\) は弾力性の大きさを意味しているので、\(log_{e}y=A\ \log_{e}x+B\) を求めようとすることはその背景に「弾力性が一定である」という前提が存在することを意味しているんです。

(※自然対数の微分公式 \((\log_{e}x)’=1/x\))
皆さんも、「まったく同じニュースや指標を見ていても、その背後にある仮定・前提が異なれば推理結果も変わって来る」のを経験したことは一度や二度ではないはず。
それと同じで、回帰分析においても「\(x\) と \(y\) の間にはどんな関係があると仮定するか」によって分析結果が変わって来る、というわけです。
経済学や自然科学の世界では「所得が1%増えるたびに需要は〇%増える」といったように弾力性が一定と考えられるものが多く存在することから、対数変換をしてから最小二乗法を使う方法がよく使われています。
どちらのモデルを使うべきか判断しにくい場合は、両方を計算して求められた決定係数 \(R^2\) (当てはまりの良さを測る尺度)が大きいモデルを選ぶという方法もあります。
その仮定・前提は本当に正しいか
回帰分析は、どの手法も何かしらの仮定・前提を踏まえたうえでの「もっともらしい」計算結果を算出しているに過ぎないので、過信は禁物です。
統計学は、正しい仮定のもとで適切なデータを使って解析した結果役に立ってきたのであって、仮定が正しくなければ数字遊びをしているのと変わりません。
もし回帰分析の計算結果に違和感があったら「データは嘘をつかないと言うし大丈夫だろう」と思わずに、「この回帰分析はどんな仮定・前提のうえに成り立っているのだろう?」「この仮定・前提は常に成り立つわけではないのかもしれない」と疑ってみることが重要です。
この記事を通じて「回帰分析の結果の意味が分かってきた」と思っていただけたら嬉しいです。
弾力性の大きさ \(A\) の値は単位に依存しないので、対数変換をしてから重回帰分析(説明変数が \(x_1,x_2,…\) と複数ある回帰分析)をすると、係数どうしの大小比較ができる( \(x_1\) のほうが \(x_2\) よりも \(y\) に与える影響が大きい等)という利点から対数変換を利用しているケースもあります。





