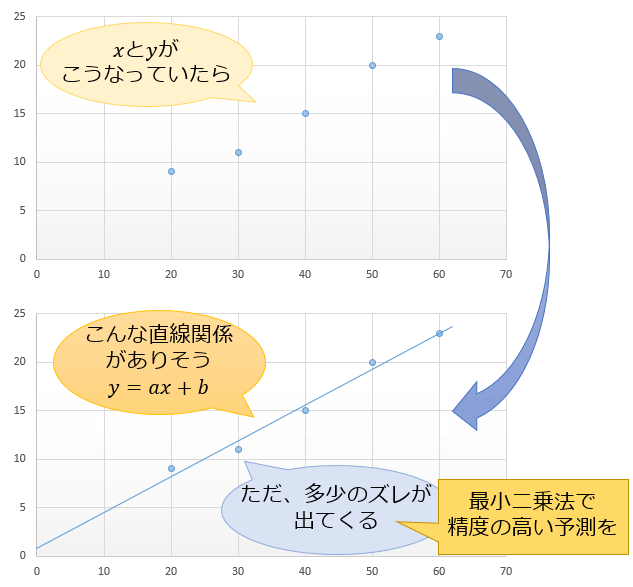
「回帰分析・最小二乗法の公式の使い方を分かりやすく解説」の記事では、最小二乗法の公式の使い方を見ていきました。

ただ、この公式。その見た目からは「なぜこの公式で回帰直線が求められるのか?」が直感的には理解しにくいため、丸暗記で使うのに抵抗があるという方も少なくないと思います。
そこで今回は、この最小二乗法の公式の求め方とその考え方について書いていこうと思います。
photo credit:Sylvain Leprovost
最小二乗法の考え方
単回帰分析とは、各 \((x_i,y_i)\) \((i=1,2,…,n)\) に \(y_i=ax_i+b+(誤差)\) という関係があると考え、その真のパラメータ \(a,b\) を推定する手法です。
真のパラメータ \(a,b\) を完璧に見極めることは出来ませんが、出来るだけ精度の高い「 \(a,b\) の推定値」 \(\hat{a},\hat{b}\) を求めることで新たな \(x_{n+1}\) から新たな \(y_{n+1}\) を予測しようというのが単回帰分析の目的です。
そのため、その直線関係を \(y=\hat{a}x+\hat{b} \) という形で予測・説明したときに、出来るだけ当てはまりの良い \(\hat{a},\hat{b}\) を探すことが目標となります。
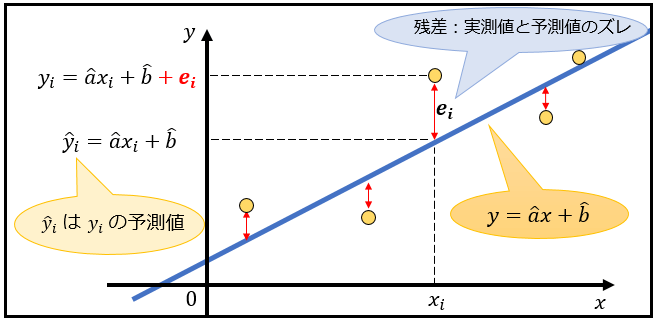
上図は、実測値(実際に得られたデータ) \(y_i\) と予測した直線による「各 \(x_i\) に対応する各 \(y_i\) の予測値」である \(\hat{y_i}(=\hat{a}x_i+\hat{b})\) のズレを表しています。
予測直線をどう引いたとしても、実測値 \(y_i\) と予測値 \(\hat{y_i}\) の間にはどこかでズレが現れることが分かりますよね。
この実測値と予測値のズレは、統計学においては「残差」と呼ばれ
\(e_i=y_i-\hat{y_i}=y_i-(\hat{a}x_i+\hat{b})\) で表されます。

こういった流れのうえで「回帰分析のために、この残差 \(e_i\) をそれぞれ2乗したものを合計した値 \(S_e\) を最小にする \((\hat{a},\hat{b})\) の組み合わせを計算することで、真のパラメータ \((a,b)\) を推定しよう」というのが最小二乗法なんです。
残差の2乗和を求めてみよう
文字だけだとピンと来にくいと思うので、具体例で残差の2乗和を計算してみましょう。
例えば、このデータの場合。

適当に、予測直線を \(y=0.35x+1\) として考えてみましょう。
\((\hat{a}=0.35,\hat{b}=1)\)
すると
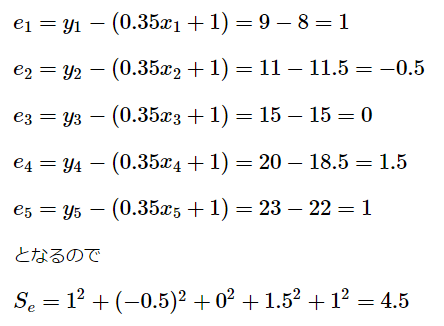
となります。
残差の2乗和を最小にする値を求めよう!
それでは、具体的に \(S_e\) を最も小さくできる \((\hat{a},\hat{b})\) を求めてみましょう。
\(S_e\) は 「\(A\hat{a}^2+B\hat{a}+C\)」 \((A>0)\)の形に変形できるので、\(S_e\) を \(\hat{a}\) で偏微分して \(0\) とおいたときの \(\hat{a}\) が「\(S_e\) を最小にする \(\hat{a}\)」となります。
\(\hat{b}\) についても同様。

この連立方程式は、以下のように式変形することで解くことができます。
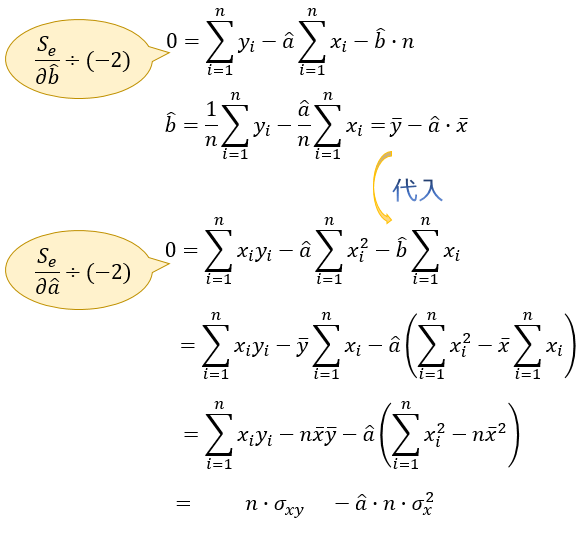
\((\hat{a},\hat{b})\) が求まり、最小二乗法の公式が求まりました。

ちなみに、今回のデータだと
\(y-15.6=\frac{74}{200}(x-40)\)
⇔ \(y=0.37x+0.8\)
となって、\(S_e=2.3\) となります。