
偏りのないサイコロを120回投げても、すべての目がちょうど20回ずつ出ることは珍しいように、確率というのは全くの偶然でも多少は偏るものです。
「A,B,C,Dについて100人にアンケートをしたらCを選ぶ人が一番多かった。だからCが一番良い!」と思っても、それは確率の偏りに惑わされているだけかもしれません。
反対に、「人は無意識下にこんなバイアスを持っている」と言われたのに対して「いやいや、自分はそんなバイアスは持っていない。ただの偶然だろう」と思っても、統計を取ってみたら偶然とは考えにくいほどの差が出ているかもしれません。
確率の偏りに惑わされないためには、「今回得られた結果は確率の偏りによって偶然得られたに過ぎないのか、それとも意味のある統計結果なのか」を判断する能力が欠かせません。
その判断材料の1つとして便利なのが、カイ二乗検定(適合度検定)です。
photo credit:brownpau
カイ二乗検定とは?
カイ二乗検定とは「帰無仮説が正しければ、検定統計量の \(\chi^2\) が近似的にカイ二乗分布に従う」ことを利用した統計的検定のことを指します。
(帰無仮説・統計量については下記記事で解説しています)

カイ二乗検定は、主に以下のような主張をする目的で行われることが多いです。
その仮説が正しいと仮定したら、\(\chi^2\) は95%の確率で△以下の値になる。
⇒しかし、今回得られた結果から計算された \(\chi^2\) の値は△を超えている。
⇒偶然 \(\chi^2\) がこんなに大きな値になったと考えるより、その仮説は正しくないと考えるほうが自然だ。
カイ二乗検定の代表的なものには、「適合度検定」・「独立性検定」・「尤度比検定」などがあります。
適合度検定と自由度
以下の式で表されるカイ二乗値 \(\chi^2\) は、帰無仮説の下で近似的に自由度 \(Φ=k-1\) のカイ二乗分布に従うことが分かっています。
これを利用して検定を行うのが、適合度検定です。
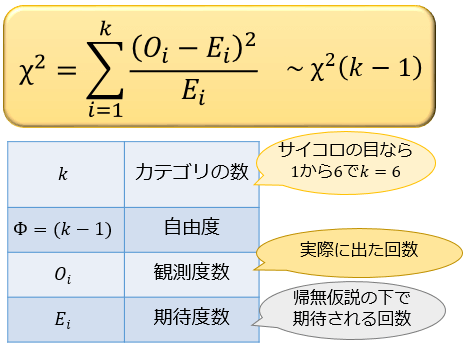
※すべての観測度数・期待度数が \(5\) 以上の値でないと近似が悪くなるので注意。
※証明は数理統計学 (数学シリーズ) p278などを参照
計算の流れ
それでは実際に、検定を行ってみます。
 By: Johan Larsson
By: Johan Larsson
「このサイコロ、偏りのあるサイコロなのでは?適合度検定で調べてみよう」
①:帰無仮説(否定したい仮説)は「H0:どの目も出る確率は \(p=1/6\)」
②:検定統計量は120回振った結果から算出される \(\chi^2\) 。有意水準は5%で片側検定する
・カテゴリの数は \(k=6\) より、自由度 \(Φ=k-1=5\) のカイ二乗分布に従う
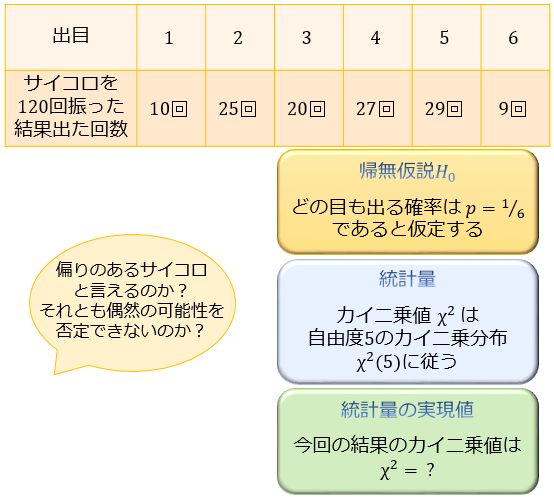
③:実際にデータを取ったところ、以下のような結果となった
④:統計量 \(\chi^2\) の実現値を算出する
・観測度数は「それぞれの目の出た回数」
・期待度数はすべて「120回 × 1/6 = 20回」(どの目も20回ずつ出ることが期待される)
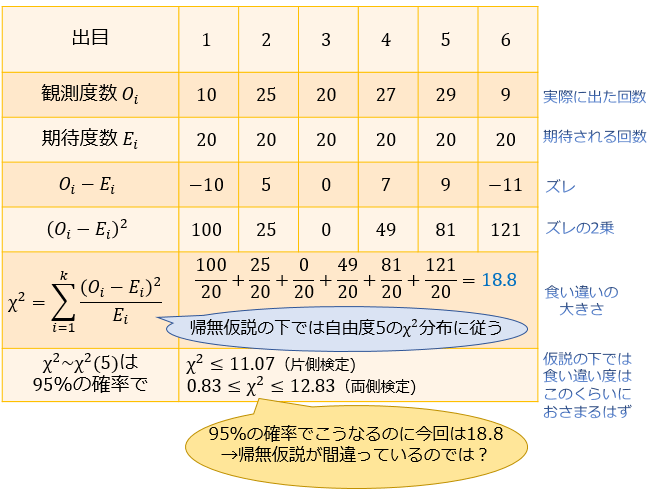
式に代入して計算すると、\(\chi^2=18.8\) と求まりましたね。
⑤:カイ二乗分布表を見て、\(\chi^2\) 値が棄却域に入っているかどうかを調べる
カイ二乗分布表を見ると、自由度5のカイ二乗分布に従う確率変数 \(\chi^2\) の上側5%点は \(11.07\) であると読み取ることができます。
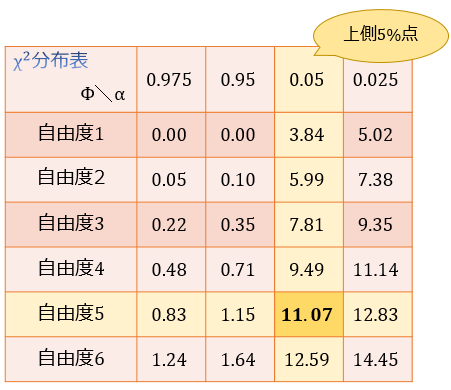
ここから、自由度5のカイ二乗分布に従う確率変数 \(\chi^2\) は95%の確率で \(\chi^2≤11.07\) となることが分かります。(片側検定)
つまり、帰無仮説の下では \(\chi^2≤11.07\) となるはずなのに、今回得られた統計量の実現値 \(\chi^2=18.8\) はその範囲を超えていることになります。
ここから、「今回得られた \(\chi^2\) の実現値は、偶然得られたとは考えにくいほど大きな値である」という結論になり、有意水準5%で帰無仮説H0が棄却されます。
統計学的に見て「このサイコロは偏りのあるサイコロであると考えられる」と主張できるだけの合理的な根拠がある、ということになります。
エクセルでの適合度検定。p値の求め方
エクセルで適合度検定をするときは、CHITEST関数が便利です。

「=CHITEST(観測度数,期待度数)」を入力した結果が0.05より低ければ、有意水準5%で帰無仮説H0が棄却されることになります。
アンケートの集計結果や顧客の購買データなど、カイ2乗検定が使える場所は数多く存在します。
確率の偏りに惑わされることなく、意味のある統計結果を見つけ出してビジネスに活用するうえで、カイ二乗検定はすごく便利な手法です。




