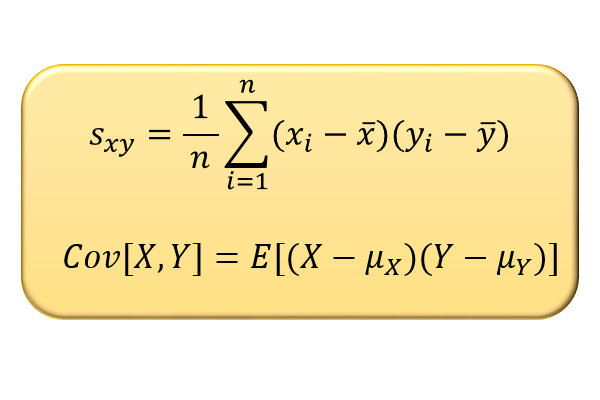いま、「成功確率60%のプランX」と「成功確率55%のプランY」があったとします。
※成功確率は母比率の意。他の条件はすべて同じと仮定
プランXを20回行って成功回数が10回以下になる確率を計算すると、約24.5%
プランYを20回行って成功回数が13回以上になる確率を計算すると、約25.2%
このように、確率というものは多少は偏るものなので、短期的には以下のようにプランYの方が好成績になるのは珍しいことではありません。
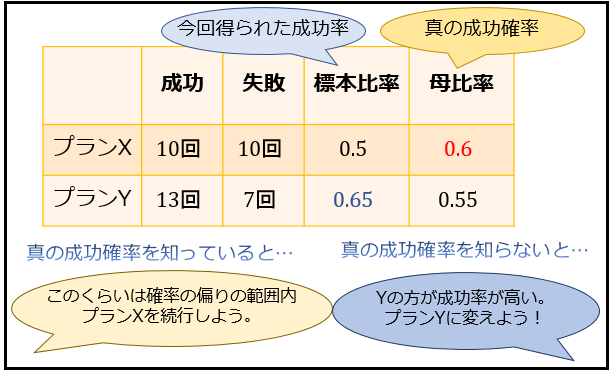
真の成功確率さえ知っていれば、「こういう事もあるさ」くらいの話ですよね。
一方で、真の成功確率を知らないと、同じ結果に対してもぼく達は「プランXよりもプランYの方が成功率が高かった。つまりプランYの方が優れているんだ!」と、つい早合点してしまいがち。
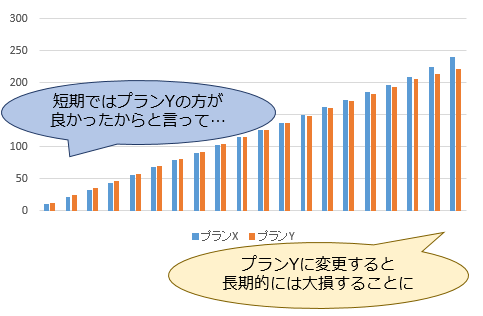
しかし、短期的にはYを選んだ方が好成績だったとしても、長期的には大数の法則によってXを選んだ方が好成績になるものです。
そのため、こういった確率の偏りに惑わされてプランYに変更してしまうと、大きな損失につながってしまうんです。
このような事態を避けるには、「今回得られた結果は確率の偏りによって偶然得られたに過ぎないのか、それとも意味のある統計結果なのか」をカイ二乗検定で確かめることが重要です。

今回のケースではカイ2乗検定のうちの1つ、「独立性の検定」を使います。
photo credit:Pistolero31
独立性の検定と自由度
カテゴリの数が \(r\) 個の属性 \(A\) と、 \(c\) 個の属性 \(B\) があったとします。
このとき、以下の式で表されるカイ二乗値 \(\chi^2\) は、「属性 \(A\) と \(B\) が独立」という帰無仮説の下で近似的に自由度 \(Φ=(r-1)(c-1)\) のカイ二乗分布に従うことが分かっています。
これを利用して検定を行うのが、独立性の検定です。

※すべての観測度数・期待度数が \(5\) 以上の値でないと近似が悪くなるので注意。
カイ二乗分布については、下記記事で詳しく解説しています。

多くのケースでは、後で紹介する \(2×2\) の簡易版公式でOKです。
計算の流れ
さっそく、冒頭の例で検定を行ってみましょう。
「プランXとプランYの成功確率に差があると言えるのか?」
①:帰無仮説(否定したい仮説)は「H0:2つのプランの成功確率に差はない」
②:検定統計量は各 \(20\) 回試行して算出した \(\chi^2\) 。有意水準は5%で片側検定する
・属性 \(A\) …プランX・Yの2種類。\(r=2\)
・属性 \(B\) …成功・失敗の2種類。\(c=2\)
よって \(\chi^2\) は自由度 \(Φ=(2-1)(2-1)=1\) のカイ二乗分布に従う
③:実際にデータを取ったところ、以下のような結果となった
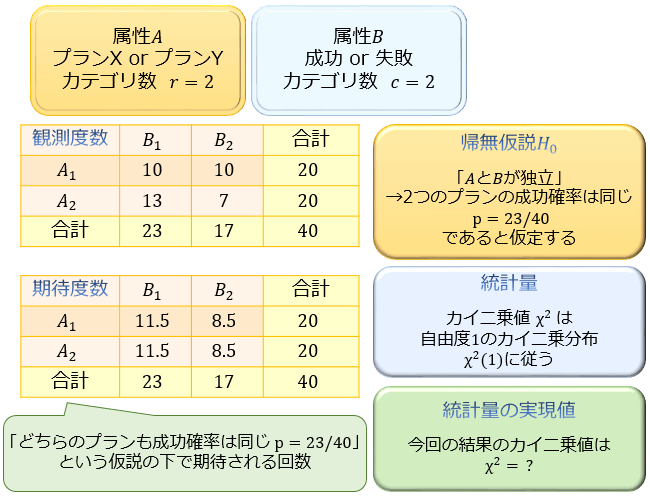
④:統計量 \(\chi^2\) の実現値を算出する
・属性 \(A\) と \(B\) が独立と仮定した場合、合計 \(40\) 回試行して \(23\) 回成功したので成功確率は \(p=23/40\) と推定される
・\(p=23/40\) より、それぞれ \(20×23/40=11.5\) 回ずつ成功して \(8.5\) 回ずつ失敗することが期待される(期待度数)
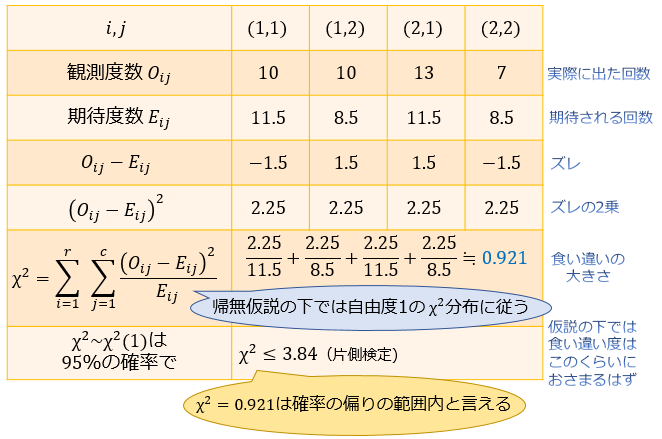
式に代入して計算すると、\(\chi^2≒0.921\) と求まりました。
次に、この値が「XとYの成功確率に差がなくても偶然得られてもおかしくない値」なのか「差がないのに偶然得られた、とは考えにくいほど大きな値」なのかを調べます。
⑤:カイ二乗分布表を見て、\(\chi^2\) 値が棄却域に入っているかどうかを調べる
カイ二乗分布表を見ると、自由度1のカイ二乗分布に従う確率変数 \(\chi^2\) の上側5%点は \(3.84\)であると読み取ることができます。
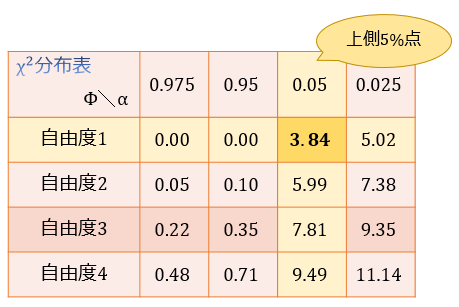
つまり、帰無仮説の下でも \(\chi^2≤3.84\) の範囲であれば多少大きな値をとってもおかしくはないことが分かります。
ここから、「今回得られた \(\chi^2≒0.921\) は、偶然得られたと考えてもおかしくない値である」という結論になり、有意水準5%で帰無仮説H0は棄却されません。
この程度の差では「YはXよりも優れている」とは言えない、ということになります。
このように検定を使えば、「母比率は X > Y なのに、たまたま標本比率が X < Y になった」場合でも、誤って「 Y の方が優れている」と判断してしまうリスクを低くおさえることができるんです。
\(2×2\) の簡易版公式
独立性の検定は、先の例のように「X or Y」と「成功 or 失敗」の \(2×2\) で検定を行うことが多いです。
この \(2×2\) の検定の場合は、先ほどの公式は以下の式に変形することができます。
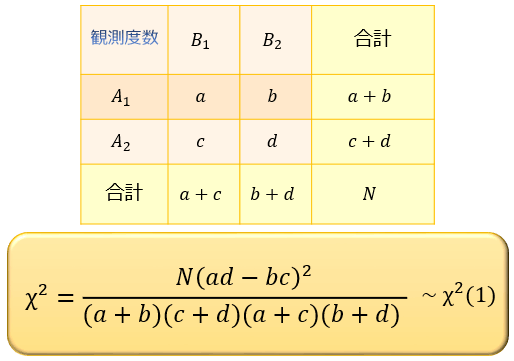
この公式から求められる値が、\(3.84\) よりも大きければ有意水準5%で帰無仮説は棄却されますし、\(3.84\) より小さければ有意水準5%で帰無仮説は棄却されません。
先の例だと、計算結果はこんな感じ。
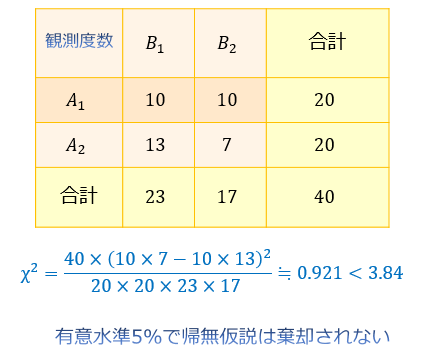
期待度数を求める手間が省けるのが嬉しいポイントですね。
計算が格段に楽になるので、\(2×2\) の独立性検定をするときはこちらの公式を使う方がオススメです。