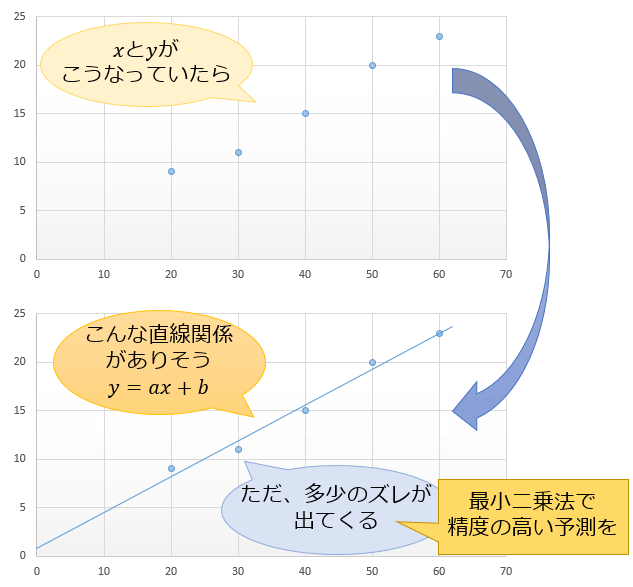
母集団が正規分布だと分かっている場合における母平均の区間推定には、「正規分布を用いた推定」と「 t 分布を用いた推定」があります。
正規分布を用いた推定とは、「母分散の値が分かっていれば、正規母集団の性質を利用して標本平均の実現値から母平均の値を推定できる」というものです。
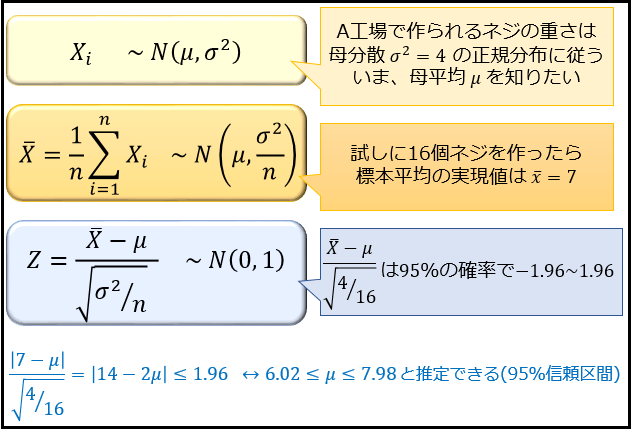
しかし、現実には「母平均 \(μ\) の値が不明なら、母分散 \(σ^2\) の値も分からない」のが普通です。
「\(σ^2\) を不偏分散(の実現値) \(u^2\) で代用する」という方法もありますが、それは「サンプルサイズ \(n\) が十分に大きければ、不偏分散は母分散に近い値をとりやすいから」なので、サンプルサイズ \(n\) が小さい場合はそれも出来ません。

そこで「母分散が未知の値であり、\(n=20\) 個程度のデータしか集められない場合に、母平均の値を推定したい」ときに利用される確率分布。
それが、t 分布です。
t検定に使われるt分布
まず、互いに独立な2つの確率変数 \(Z\) と \(W\) を考えます。
\(Z\) が標準正規分布 \(N(0,1)\)に従い、\(W\) が自由度 \(m\) のカイ二乗分布に従うとき、確率変数 \(T=\frac{Z}{\sqrt{W/m}}\) が従う確率分布を自由度 \(m\) の t 分布と呼び、\(T\sim t(m)\) と表記されます。

この t 分布を用いて「平均の差」について行う検定を t 検定と言います。
(正規分布・カイ2乗分布については下記記事を参照)


t分布の確率密度関数
自由度 \(m\) の t 分布の確率密度関数は、以下の式で表されます。

標本平均と不偏分散から母平均を推定する
さて、\(T=\frac{Z}{\sqrt{W/m}}\) が従う確率分布を理解すると、どんなメリットがあるのでしょうか。
その答えは、「母集団が正規分布であることさえ分かれば、母分散が分からなくても標本データから算出できる標本平均と不偏分散(の実現値)から母平均を推定できるようになる」ことにあります。
初めに述べた通り、\(Z=\frac{\overline{X}-μ}{\sqrt{σ^2/n}}\) では \(σ^2\) の値が分からないので、そのままだと母平均 \(μ\) の推定には使えません。
そこで、「母分散 \(σ^2\) と不偏分散 \(U^2\) の比 \(\frac{(n-1)U^2}{σ^2}\) 」を利用します。
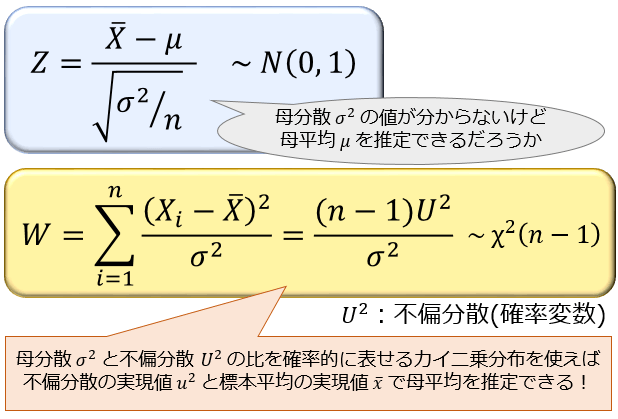
\(\overline{X}\):標本平均(確率変数) , \(U^2\):不偏分散(確率変数)
\(\overline{x}\):標本平均の実現値 , \(u^2\):不偏分散の実現値
実は、正規母集団において、確率変数としての不偏分散 \(U^2\) を \((n-1)/σ^2\) 倍した値は、\(Z=\frac{\overline{X}-μ}{\sqrt{σ^2/n}}\) と独立で、自由度 \(n-1\) のカイ二乗分布に従うことが分かっています。(※)
この性質を利用して、自由度 \(m=n-1\) の t 分布に従う確率変数 \(T=\frac{Z}{\sqrt{W/(n-1)}}\) の \(Z\) と \(W\) に、これらを代入してみましょう。
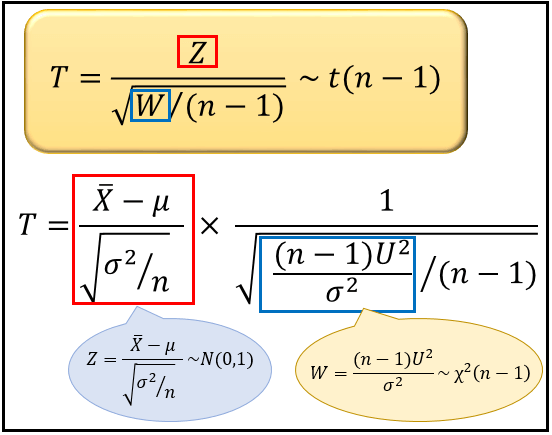
すると、\(n-1\) と \(σ^2\) がキレイに消えて、\(\frac{\overline{X}-μ}{\sqrt{U^2/n}}\) が自由度 \(n-1\) の t 分布に従うことが分かります。
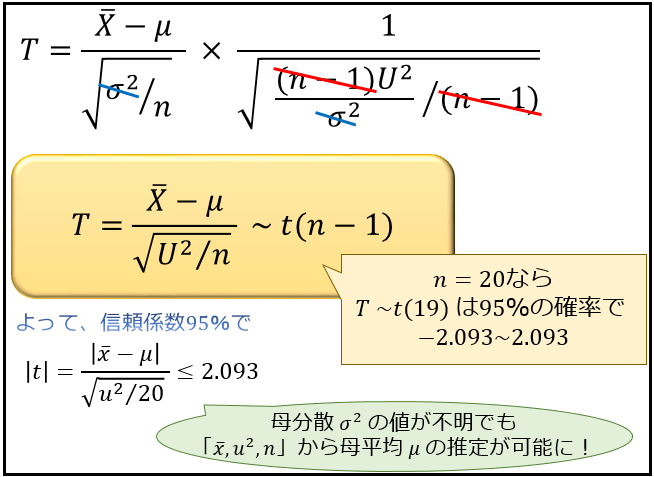
つまり、t 分布を理解しておけば、\(\frac{\overline{X}-μ}{\sqrt{U^2/n}}\) がどのくらいの確率でどんな値をとるのかが分かるようになるわけです。
たとえば、自由度 \(19\) の t 分布に従う確率変数は95%の確率で \(-2.093≤T≤2.093\) の値をとります。(t分布表より)
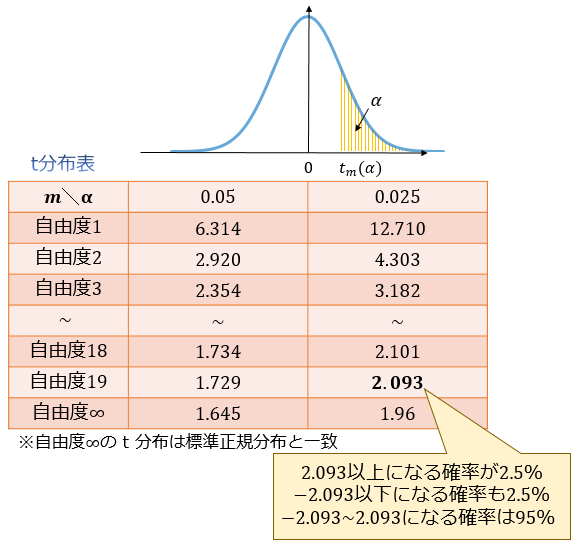
ここから、サンプルサイズ \(n=20\) の標本から計算される \(\frac{|\overline{x}-μ|}{\sqrt{u^2/20}}\) も\(2.093\) より小さな値であると信用することには一定の合理性があることが分かります。
これにより、例えば標本平均 \(\overline{x}=40\) ,不偏分散 \(u^2=20\) と求まったなら、信頼係数95%で \(\frac{|40-μ|}{\sqrt{20/20}}≤2.093\) ⇔ \(37.907≤μ≤42.093\) と推定できます。
(これを95%信頼区間と言います)
このように、t 分布は母平均を推定したいときに重宝する確率分布となっているのです。
95%信頼区間の解釈
95%信頼区間の意味はややこしいので、注意しておきたいところ。
×(間違い)「95%の確率で \(37.907≤μ≤42.093\) 」
→母平均 \(μ\) は定数です。確率的に変動するのは信頼区間の方です。「意外な調査結果であるほど公表されやすい」というバイアスがある以上、「公表された100個の95%信頼区間のうち正しいのは80個だけだった」というケースは十分ありえます。
◎(正しい)「100回に95回の割合で母平均を含む推定をしたら \(37.907≤μ≤42.093\) と求まった。この範囲に母平均が含まれていると信頼することには一定の合理性がある」
これについては「標準誤差とは何なのか。95%信頼区間から分かる推定精度のおはなし」の記事も参考にしてみてください。
t 分布は、ビール会社のギネス社に勤務していたゴセットという科学者が、サンプルサイズ \(n\) を大きくできない制約の中でも何とか上手く推定できないか悪戦苦闘した結果生まれた「実務の視点から登場した分布」です。
ぼくも初めて聞いた時は「こんな複雑な分布を考えなくても、正規分布で十分じゃないの?」なんて思っていましたが、いまは統計学において無くてはならない存在だと感じます。