コインを投げると、試行結果は基本的に「表」か「裏」かの2通りだけですよね。
※試行:コイン投げのように同じ条件で何度も繰り返す事ができ、その結果が偶然により決まる実験・観測のこと
このように、試行結果が「〇 か × か」や「成功か失敗か」といった2種類しかない試行のことを、統計学ではベルヌーイ試行と呼びます。
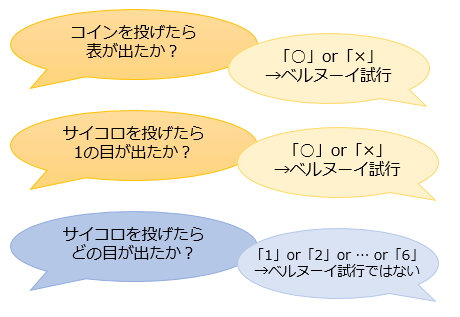
ここで「互いに独立したベルヌーイ試行を n 回行ったときにある事象が何回起こるかの確率分布」のことを、二項分布と言います。※英語では Binomial Distribution
たとえば、
「30%の確率で表が出る特殊なコインを 4 回投げたときに、表が k 回でる確率の分布」
「サイコロを200回投げたときに、1の目が k 回でる確率の分布」
などが二項分布にあたります。
エクセルでは、BINOM.DIST関数で求められます。

二項分布は、その定義や数式をみるとややこしく感じるかもしれませんが、
具体例を通じて考えれば非常に使いやすくてわかりやすい分布です。
今回は、そんな二項分布の性質について、「正規分布やポアソン分布との違い・関係性・近似法」も交えて解説していきます。
photo credit:motoyen
二項分布とは?その確率関数
二項分布とは、互いに独立したベルヌーイ試行(成功確率\(= p\) , 失敗確率\(= 1-p\) )を \(n\) 回繰り返したときの成功回数に関する離散確率分布のこと。
二項分布は \(B(n, p)\) または \(Bin(n, p)\) と表記され、以下の確率関数で表されます。

また、ある確率変数 \(X\) が二項分布 \(B(n, p)\) に従う場合、『\(X \sim B(n, p)\)』と表記されます。
二項分布でまずおさえておきたいのが、確率関数の使い方です。
例えば、「30%の確率で表がでる特殊なコインを 4 回投げたときに、表が \(k\) 回でる確率の分布」は、この確率関数に \(n = 4 , p = 0.3\) を代入することで以下のように求められます。
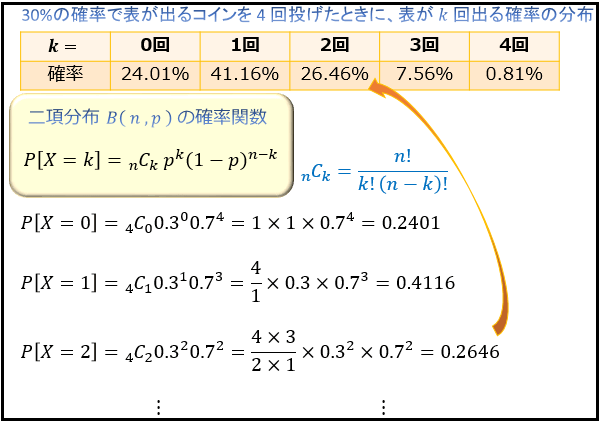
確率関数は「確率 \(p\) で起きることが \(k\) 回」「確率 \((1-p)\) で起きることが \((n-k)\) 回」あって、そのパターンが「全部で \(_{n}C_{k}\) 通り存在する」と考えると覚えやすいです。
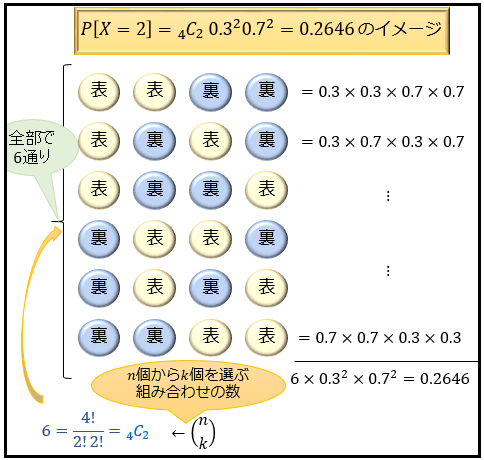
二項分布の平均(期待値)と分散・標準偏差の導出
二項分布 \(B(n, p)\) に従う確率変数 \(X\) の期待値は \(np\) 、分散は \(np(1-p)\)、標準偏差は分散の平方根で表されます。
期待値とは、例えば「30%の確率で表が出るコインを4回投げたら平均的には何回表が出るか」を表す値ですから \(n×p=np ⇔ 4×0.3=1.2\) となります。
分散の考え方としては
\(i\) 回目に失敗したら \(0\) ・成功したら \(1\) をとる確率変数を \(X_i (i=1,2,\cdots,n)\) としたとき、
\(X_i\) の期待値は \(E[X_i]=0×(1-p)+1×p=p\)
\(X_i\) の分散は「偏差の2乗の期待値」なので
\(V[X_i]=p^2×(1-p)+(1-p)^2×p\)
\(=p×(1-p)×(p + 1-p)=p(1-p)\)
そして、確率変数 \(X\) はこれを \(n\) 回繰り返したものなので
\(V[X]=V[X_1+X_2+\cdots+X_n]\)
\(=V[X_1]+\cdots+V[X_n]=np(1-p)\)
になる、というわけです。

「難しくてピンとこない…」場合でも、とりあえず期待値は \(np\) ,分散は \(np(1-p)\) と暗記しておくと便利です。
np(1-p) が十分大きいと正規分布に近似
たとえば、「サイコロを200回投げたときに、1の目は何回くらいでるものなのか?」を考えてみましょう。
(試行回数 \(n=200\)、成功確率 \(p=1/6\))
 By: Edwin Torres
By: Edwin Torres
期待値的には大体 \(200×1/6 ≒33.3\) より33回か34回くらい出そうですが、標準偏差の記事でも書いた通り、平均(期待値)はそれ単体ではあまり役に立ちません。
期待値だけでは「30回以下しか出ないケースや、40回以上出るケースは珍しいことなのか?」が分からないんです。
これを正確に調べるには二項分布の確率関数を使う事になるのですが、試行回数が \(n=200\) と非常に大きいため、\(_{n}C_{k}\) や \(p^k\) の計算量が膨大でコンピュータでもないと計算できません。
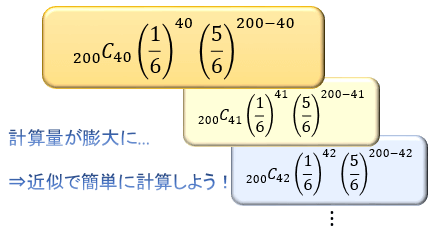
そこで役に立つのが、正規分布による近似(正規近似・ラプラスの定理)です。
実は、二項分布は分散 \(np(1-p)\) が十分に大きければ、下図のような形・確率密度関数をした正規分布として近似できるという性質があるんです。
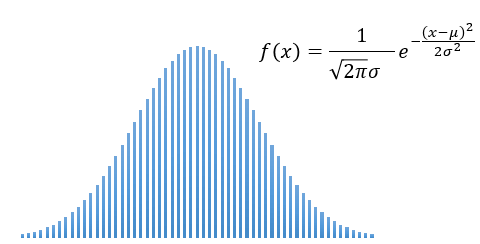
※ μ[平均]=np , σ2[分散]=np(1-p)
正規分布に近似できれば、「正規分布とは何なのか?その基本的な性質と理解するコツ」の記事でも書いた通り、「平均との差が標準偏差何個分か?」という視点でみることにより、楽に確率を求められます。
具体的な計算法は、以下の通り。

以上から、「200回サイコロを投げたときに1の目が出る回数」は
約68%の確率で28回~38回におさまり
約87%の確率で26回~41回におさまり
約95%の確率で23回~44回におさまる
ということが分かりました。
正規近似は概算値ではありますが、計算量が格段に減る便利なテクニックです。
ぜひ、覚えておきたいところ。
二項分布と正規分布の違いによる誤差と、近似基準
ここで、近似というと
「正確な値と比べてどのくらい誤差が出るんだろう?」
「 \(np(1-p)\) がいくつ以上なら近似しても大丈夫なの?」
と気になる方もいるかと思います。
そこで、コンピュータを使って「200回サイコロを投げたときに1の目が出る回数」に関する正確な出現確率を調べてみると
正規分布が、精度の高い近似になっていることが分かります。
近似基準としては
① \(min(np,n(1-p))>10\)
② \(0.1≤p≤0.9\) かつ \(np(1-p)>5\)
③ \(np(1-p)>25\)
の3通り存在します。(出典:統計分布ハンドブック)
今回は、一番厳しい基準の③を満たしているおかげで、精度の高い近似になっているということですね。
nが大きくpが小さいとポアソン分布に近似
\(np(1-p)\) がそこまで大きくはなく、上述の近似基準を満たさない場合、正規近似を使うことはできません。
しかし、そういう場合でも \(n\) が十分に大きく、\(p\) が十分に小さいときはポアソン分布に近似することができます。
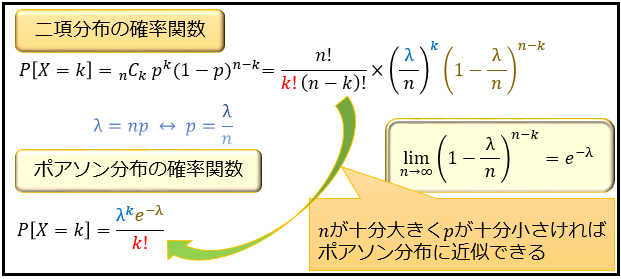
ネイピア数の記事でも書きましたが、例えば「2分に平均1回起きる現象」というのは
①「1分ごとに、50%の確率で起きるかどうかの判定が行われている」というよりも
②「限りなく短い時間ごとに、限りなく小さい確率で起きるかの判定が行われている」
と考えた方がより的確に実態を表わしていると考えられるので、二項分布よりポアソン分布のほうが適しているんです。
具体的な計算方法については、「ポアソン分布とは何か。その性質と使い方を例題から解説」の記事をご参照ください。
適している計算対象の違い
\(n\):試行回数 \(p\):成功確率
①二項分布を使った計算:コイン投げのように \(0.1≤p≤0.9\) で、 \(n≤20\) のときに特に便利(コンピュータを使うなら \(n\) がもっと大きくてもOK)
②正規分布を使った計算:200回のサイコロ投げのように \(n\) が大きく \(np(1-p)≥25\) のときに便利
③ポアソン分布を使った計算:「単位時間あたりに、ある現象が何回起こるか」のように \(p\) が非常に小さい値のときに便利
世の中の多くの現象は「○か×か」の積み重ねで出来ているため、二項分布と正規近似・ポアソン近似を理解すれば色んな現象の確率を求められます。ぜひ、マスターしてください!