数列の和を求めるとき、式変形をするたびに毎回数列をすべて書いていたら、スペースがいくらあっても足りません。
そのため、多くの場合は総和記号 Σ (シグマ)を使ってまとめて計算することになります。

Σ の式は、k に「k = 1,2,3,…,n-1,n」をそれぞれ代入した n 個の数列の合計を意味する式です。
(k の代わりに i や j を使うことも多いです)
Σ を使った計算をするときは、頭の中で k = 1 から n までを代入した数列をイメージしながら計算すると良いでしょう。

今回は、そんな Σ にまつわる公式について書いていきます。
photo credit:docmonstereyes
知っていると便利な5つの公式
Σ (シグマ)を使った計算では、覚えておくと便利な公式がいくつかあります。
ここでは、以下の5つの公式について軽く解説していきます。
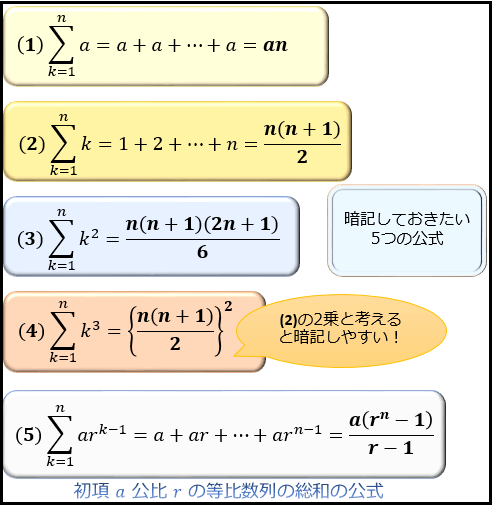
(1) a が n 個並んだ数列
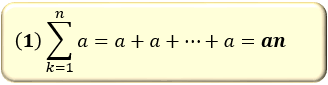
(1)は、a が n 個並んだ数列「a + a + … + a」をイメージしたら分かる通り、a の n 倍になります。
「k に何を代入しても a は a のまま」と考えると分かりやすいです。
(2) 1 から n までの総和
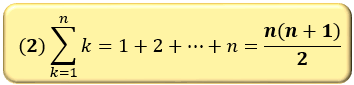
(2)は 1 から n までの数字をすべて足した値を意味しています。
数学者カール・フリードリヒ・ガウスが小学生のとき「1から100までの数字をすべて足しなさい」という課題を出され、「1+100=101、2+99=101、…、50+51=101」となるので答えは101×50=5050、と即答して教師を驚かせた逸話で有名な公式です。
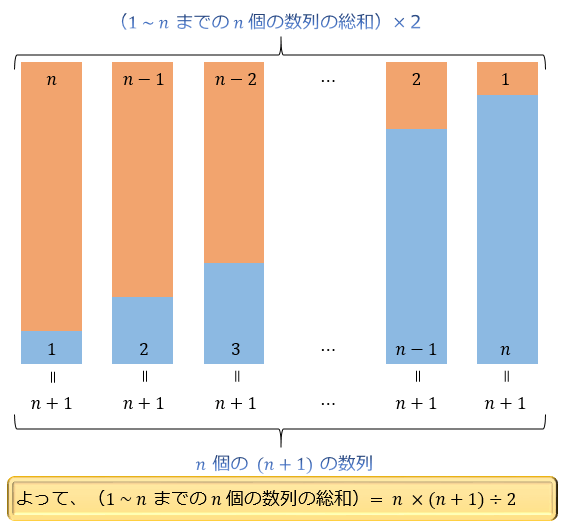
この公式は、1 から n までの数字の総和を「S」とおいたときに「Sの2倍」がちょうど(n+1)を n 回足したのと同じになることをイメージすると覚えやすくなります。
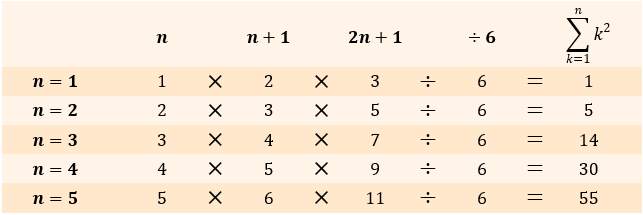
(3),(4) 2乗・3乗の公式
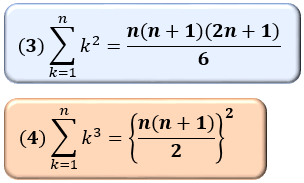
(3),(4)の公式は直感的な理解が難しく、丸暗記したほうが早いです。
特に(3)はド忘れしやすいので、何回も使って頭に叩き込む必要があります。
反復練習あるのみ!
一方、(4)はちょうど「(2):1 から n までの総和」の公式の2乗なので、(2)を覚えておけば簡単に暗記できますね。
参考:(3)の証明方法

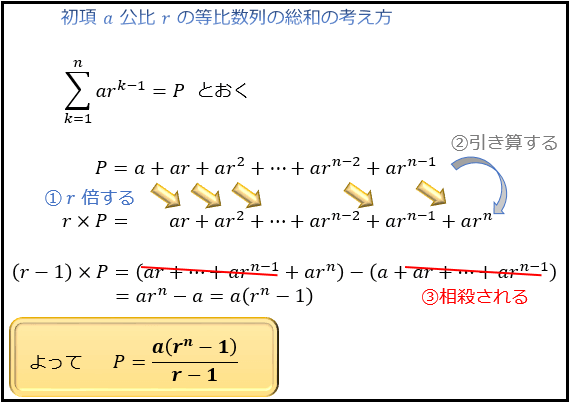
(5)等比数列の第n項までの総和

最後は、初項 a 公比 r の等比数列の第n項までの総和の公式 (※ r ≠ 1 )
n の式だとややこしそうに見えるかもしれませんが、実際に n =2 , 3 を代入するとキチンと等比数列の総和になっているのが分かります。
この公式は、初項 a 公比 r の等比数列の第n項までの総和を「P」とおいたときに「Pの r 倍」から「P」を引くと「初項と末項」以外のすべての項が消えるのをイメージすると覚えやすくなりますよ。