「\(a\) を何乗したら \(x\) になるか」を表す数、対数。
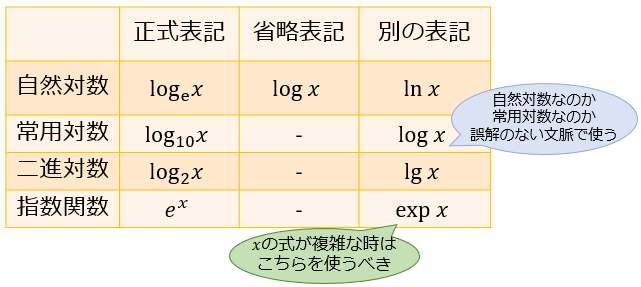
対数は、底 \(a\) と真数 \(x\) を使って \(\log_{a}x\) と書くのが正式な表記です。
例えば「\(2\) を何乗したら \(8\) になるか」を表す数は、 \(\log_{2}8=3\) となります。
ただ、 「底を明示しなくても文脈的に誤解がない」と判断された場合には、\(\log\ x\) といったように底 \(a\) を省略して表記されることが多いです。
今回は、そんな対数の省略表記・使い分けについて書いていきます。
自然対数 log,ln
まず、ネイピア数 \(e≒2.718\) を底とする対数 \(\log_{e}x\) のことを自然対数と言います。
自然対数 \(\log_{e}x\)は「\(e≒2.718\) を何乗したら \(x\) になるか」を表しています。
\(\log_{e}x\) は、微分すると \(1/x\) になるという特徴があり、数理上の複雑な計算をするうえで非常に便利な対数です。

(詳しくは下記記事にて)
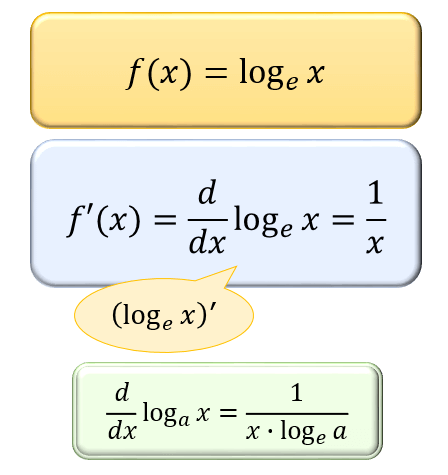
そのおかげもあって、数学や統計学の世界では対数というと自然対数を指すことが多く、 \(\log_{e}x\) を \(\log\ x\) と省略して表記することも多いです。
ただし、欧米などでは \(\log_{e}x\) のことは \(\ln\ x\) と表記することが多いですね。
関数電卓でも \(\log_{e}x\) の計算には「\(\ln\)」が対応しているので、ご注意を。
\(\ln\) は natural logarithm(自然対数)の頭文字から
常用対数 log
次に、\(10\) を底とする対数 \(\log_{10}x\) のことを常用対数と言います。
自然対数 \(\log_{10}x\)は「\(10\) を何乗したら \(x\) になるか」を表しています。
常用対数は10進数と関連付けやすく、実際に値を求める際に便利なので、生物・化学・工学の世界では \(\log_{10}x\) を\(\log\ x\) と省略して表記することが多いです。

また、欧米などでは数学においても \(\log_{10}x\) を \(\log\ x\) と表記することが多いです。
関数電卓でも \(\log_{10}x\) の計算には「\(\log\)」が対応しています。
二進対数 lg,lb,ld
\(2\) を底とする対数 \(\log_{2}x\) のことを二進対数と言います。
二進対数 \(\log_{2}x\)は「\(2\) を何乗したら \(x\) になるか」を表しています。
「電気信号ON\(=1\)」「電気信号OFF\(=0\)」の2進数で成り立っているコンピュータの世界で重宝される対数で、情報理論などの分野でよく使われています。
 By: Perica
By: Perica
二進対数 \(\log_{2}x\) は \(lg\ x\) と短く表記されることが多いですが、他にも \(lb\ x\) や \(ld\ x\) といった表記もありますし、単に \(\log\ x\) と表記されることもあります。
指数関数 exp
ネイピア数 \(e≒2.718\) を \(x\) 乗した数 \(e^x\) のことを、指数関数と言います。
\(e^x\) は \(exp(x)\) と表記されることもあります。
指数 \(x\) がシンプルな時は \(e^x\) と表記されるのが一般的ですが、\(e^{-\frac{(x-μ)^2}{2σ^2}}\)のように複雑な式の場合、指数として右上に小さく書くと読みにくいので、 \(exp(-\frac{(x-μ)^2}{2σ^2})\) と表記されます。
統計学では正規分布を始め、様々な分布の関数で登場するので、ぜひ覚えておきたいところ。


\(\log\ x\) は、数学・統計学では自然対数 \(\log_{e}x\)
生物・化学・工学では常用対数 \(\log_{10}x\)
欧米や関数電卓でも常用対数 \(\log_{10}x\)
情報理論では二進対数 \(\log_{2}x\)
ぼくも初めは戸惑いましたが、少しずつ慣れていけば大丈夫です!