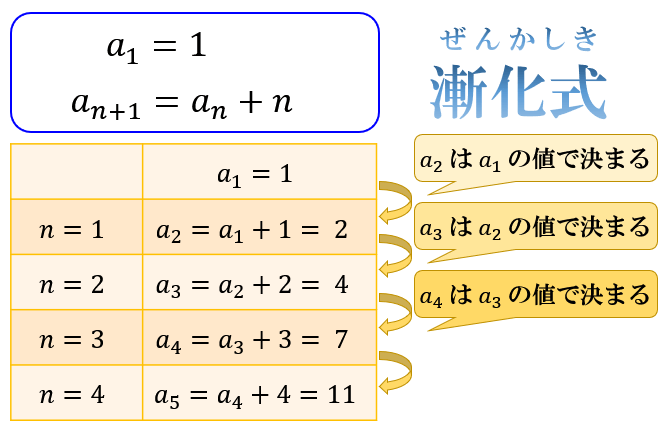
今回は、等差数列・等比数列・階差数列型のどのパターンにも当てはまらない漸化式の解き方を見ていきます。
等差数列・等比数列・階差数列型については「漸化式とは。等差数列・等比数列・階差数列の意味と一般項を求める公式」の記事で解説しています。
特殊解型
まず、おさえておきたいのが \(a_{n+1}=pa_n+q\) \((p≠1,q≠0)\) の形の漸化式。
等差数列・等比数列・階差数列型のどのパターンにも当てはまらないので、コツを知らないと苦戦する漸化式です。
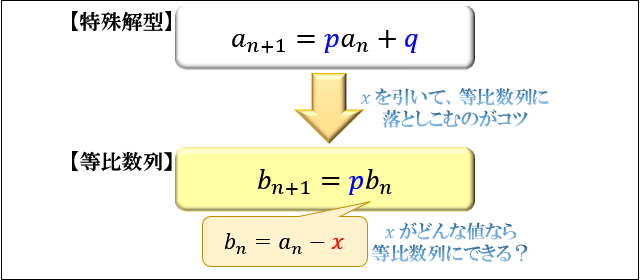
たとえば、\(a_1=2\) , \(a_{n+1}=3a_n-2\) という漸化式の場合。
数列にすると \(2,4,10,28\cdots\) という並びになり、一般項を求めるのは難しそうですよね。
しかし、この数列の各項から \(1\) を引くとどうでしょう?
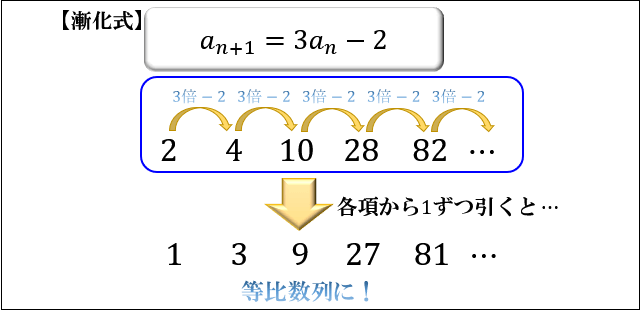
\(1,3,9,27,\cdots\) で、初項 \(1\) , 公比 \(3\) の等比数列になっていることが分かりますよね。
等比数列にさえなってしまえばこちらのもの。
等比数列の一般項の公式に当てはめることで、ラクに一般項を求めることができます。
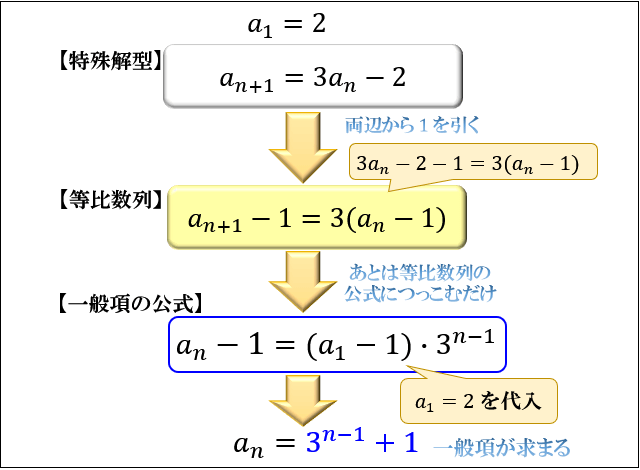
一般項が \(a_n=3^{n-1}+1\) と求まりましたね。
さて、 「 \(a_n\) から引くことで等比数列 \(b_n\) に変形できる数 \(x\) 」さえ見つかれば、簡単に一般項を求められることは分かりました。
では、その \(x\) はどうすれば見つかるのでしょうか?
その答えは、\(x=px+q\) を解くことにあります。

\(x=px+q\) を満たす \(x\) さえ見つかれば、上図のように元の漸化式の左辺から \(x(=px+q)\) を引くことで、等比数列を作ることができます。
この \(x=px+q\) のことを、特性方程式と言います。
特性方程式は「漸化式をカンタンに解くために必要な値 \(x\) を求める方程式」です。
【問①】\(a_1=3\) , \(a_{n+1}=4a_{n}-6\) で定められる数列 \( \left\{a_n \right\}\) の一般項を求めてください。
特性方程式 \(x=4x-6\) を満たす \(x\) は \(x=2\) なので、
この漸化式は両辺から \(2\) を引くと等比数列に変形できることが分かります。
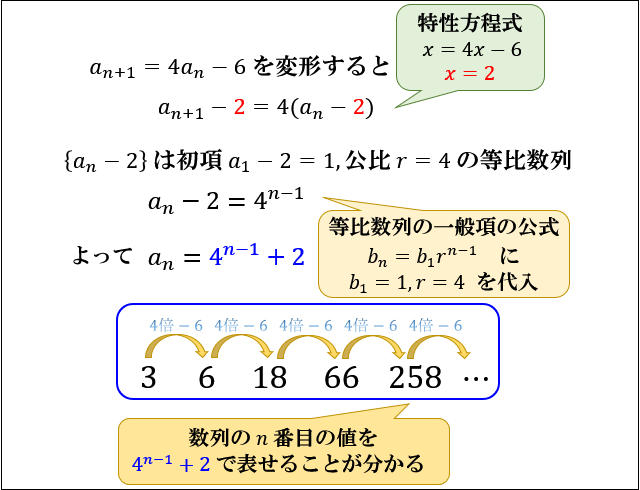
等比数列の一般項の公式に代入することで
一般項 \(a_n=4^{n-1}+2\) が求まりました。
実際に数列をみると
\(n=4\) 番目の値が \(4^3+2=66\)
\(n=5\) 番目の値が \(4^4+2=258\)
と一般項で数列を表せていることが分かりますね。
変形すると特殊解型になるパターン
ここからは、さらに複雑なパターンの漸化式を紹介します。
どのパターンでも、上手く変形してさきほどの「特殊解型」に持ち込むのがコツです。
\(n+2\) 番目と \(n+1\) 番目の差をとる
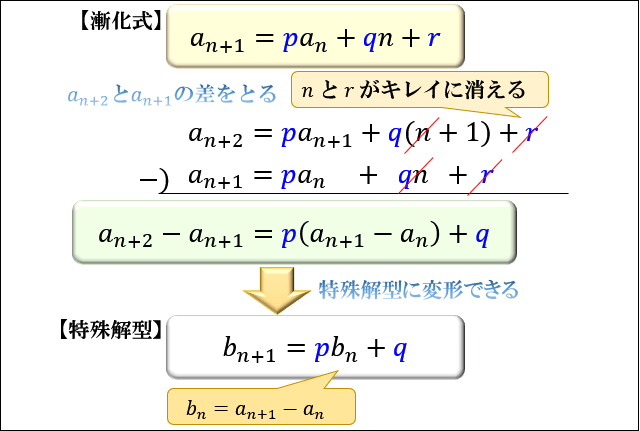
\(a_{n+1}=pa_n+qn+r\) の形のときは
\(a_{n+2}\) と \(a_{n+1}\) の差をとって \(n,r\) を消すのがコツ。
\(b_n=a_{n+1}-a_n\) とおくことで、特殊解型に変形することができます。
【問②】\(a_1=2\) , \(a_{n+1}=3a_{n}-2n+1\) で定められる数列 \( \left\{a_n \right\}\) の一般項を求めてください。

\(a_{n+1}=3a_{n}-2n+1\)
⇒特殊解型 \(b_{n+1}=3b_n-2\)
⇒等比数列 \(b_{n+1}-1=3(b_n-1)\)
⇒階差数列型 \(a_{n+1}-a_{n}=2×3^{n-1}+1\)
と変形していくことで
一般項 \(a_n=3^{n-1}+n\) が求まりました。
等比数列の一般項の公式に加えて、階差数列型の一般項の公式や等比数列の総和の公式も使う手強い問題ですね。
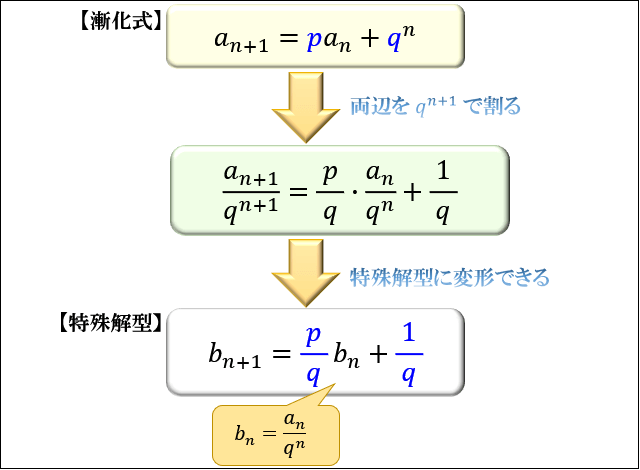
\(q^n\) で割る
\(a_{n+1}=pa_n+q^n\) の形のときは
両辺を \(q^n\) で割ってから \(b_n=\dfrac{a_n}{q^n}\) とおくのがコツ。
【問③】\(a_1=3\) , \(a_{n+1}=2a_{n}+2×3^n\) で定められる数列 \( \left\{a_n \right\}\) の一般項を求めてください。

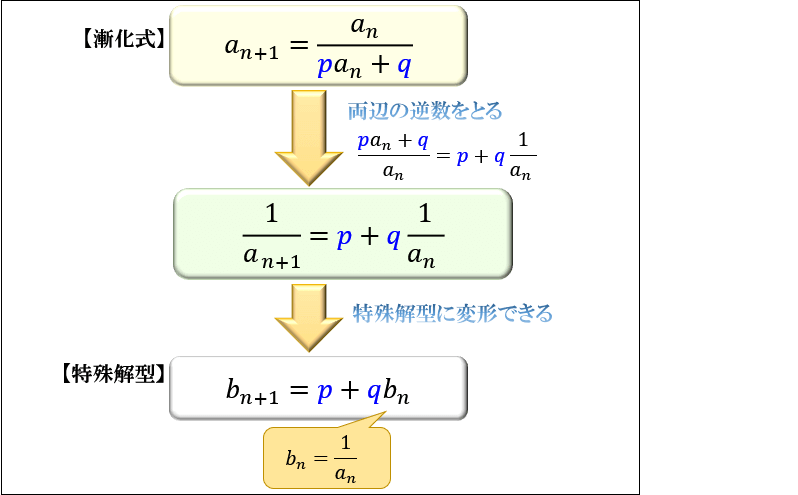
逆数をとる
\(a_{n+1}=\dfrac{a_n}{pa_n+q}\) の形のときは
両辺の逆数をとってから \(b_n=\dfrac{1}{a_n}\) とおくのがコツです。
\(a_n=0\) だと \(b_n\) を定義できないので、すべての自然数 \(n\) について \(a_n≠0\) であることを示しておく必要があります。
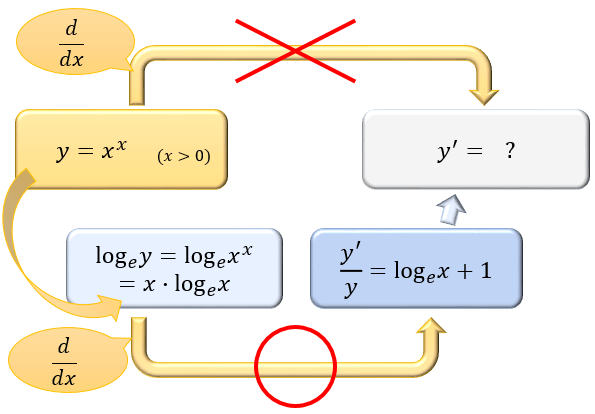
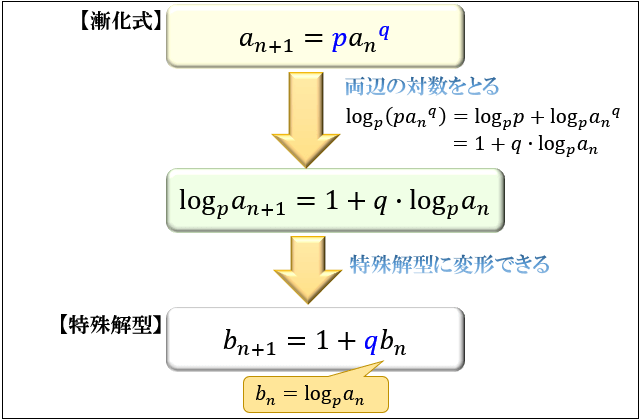
対数をとる
\(a_{n+1}=pa_n^q\) の形なら
両辺の対数をとってから \(b_n=\log_p{a_n}\) とおきます。
\(a_n≦0\) だと \(b_n\) を定義できないので、すべての自然数 \(n\) について \(a_n>0\) であることを示しておく必要があります。